原文链接: https://leetcode-cn.com/problems/sum-of-root-to-leaf-binary-numbers

英文原文

You are given the root of a binary tree where each node has a value 0 or 1.  Each root-to-leaf path represents a binary number starting with the most significant bit.  For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.

For all leaves in the tree, consider the numbers represented by the path from the root to that leaf.

Return the sum of these numbers. The answer is guaranteed to fit in a 32-bits integer.

 

Example 1:

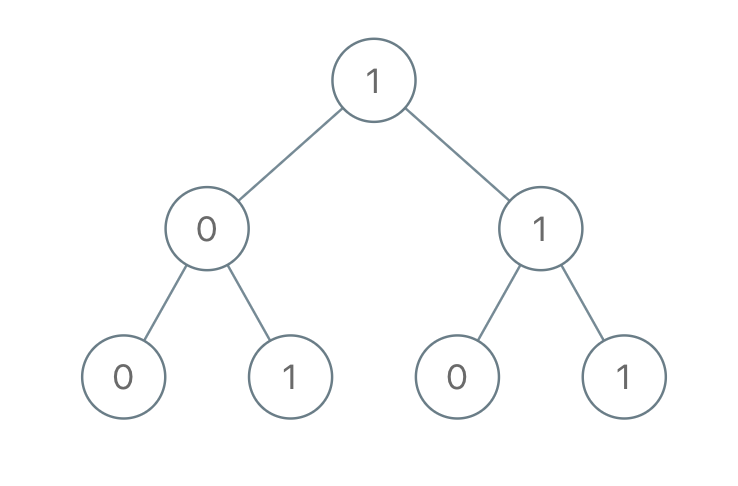
Input: root = [1,0,1,0,1,0,1]
Output: 22
Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

Example 2:

Input: root = [0]
Output: 0

Example 3:

Input: root = [1]
Output: 1

Example 4:

Input: root = [1,1]
Output: 3

 

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• Node.val is 0 or 1.

中文题目

给出一棵二叉树，其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。例如，如果路径为 0 -> 1 -> 1 -> 0 -> 1，那么它表示二进制数 01101，也就是 13 。

对树上的每一片叶子，我们都要找出从根到该叶子的路径所表示的数字。

返回这些数字之和。题目数据保证答案是一个 32 位 整数。

 

示例 1：

输入：root = [1,0,1,0,1,0,1]
输出：22
解释：(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

示例 2：

输入：root = [0]
输出：0

示例 3：

输入：root = [1]
输出：1

示例 4：

输入：root = [1,1]
输出：3

 

提示：

• 树中的结点数介于 1 和 1000 之间。
• Node.val 为 0 或 1 。

通过代码

高赞题解

解题思路：

从根节点开始遍历，每向下一个节点，我们可以把父节点传入的值左移一位并或上当前节点的值。

int newVal = val<<1 | node.val;

这样我们就得到了一个从根节点到当前节点表示的数值。接下来我们要做的只是判断一个节点是不是叶子节点，如果是的话就累加，否则继续。思路还是很清晰的。代码如下：

public void dfs(TreeNode node,int val){
        if (node == null) return;

        int newVal = val<<1 | node.val;
        
        if (node.left == null && node.right == null){
            sum += newVal ;
        }else{
            dfs(node.left,newVal);
            dfs(node.right,newVal);
        }
    }

调用的时候，原始值我们传入 0 即可。
代码如下：

public int sumRootToLeaf(TreeNode root) {
        dfs(root,0);
        return sum % mod;
    }

每个节点遍历一次，时间复杂度 $O(N)$，不需要额外的存储空间，空间复杂度 $O(1)$。

统计信息

通过次数	提交次数	AC比率
20823	29434	70.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言