原文链接: https://leetcode-cn.com/problems/distance-between-bus-stops

英文原文

A bus has n stops numbered from 0 to n - 1 that form a circle. We know the distance between all pairs of neighboring stops where distance[i] is the distance between the stops number i and (i + 1) % n.

The bus goes along both directions i.e. clockwise and counterclockwise.

Return the shortest distance between the given start and destination stops.

 

Example 1:

Input: distance = [1,2,3,4], start = 0, destination = 1
Output: 1
Explanation: Distance between 0 and 1 is 1 or 9, minimum is 1.

 

Example 2:

Input: distance = [1,2,3,4], start = 0, destination = 2
Output: 3
Explanation: Distance between 0 and 2 is 3 or 7, minimum is 3.

 

Example 3:

Input: distance = [1,2,3,4], start = 0, destination = 3
Output: 4
Explanation: Distance between 0 and 3 is 6 or 4, minimum is 4.

 

Constraints:

• 1 <= n <= 10^4
• distance.length == n
• 0 <= start, destination < n
• 0 <= distance[i] <= 10^4

中文题目

环形公交路线上有 n 个站，按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离，distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。

环线上的公交车都可以按顺时针和逆时针的方向行驶。

返回乘客从出发点 start 到目的地 destination 之间的最短距离。

 

示例 1：

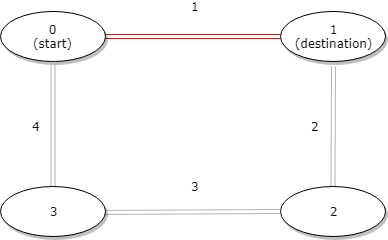
输入：distance = [1,2,3,4], start = 0, destination = 1
输出：1
解释：公交站 0 和 1 之间的距离是 1 或 9，最小值是 1。

 

示例 2：

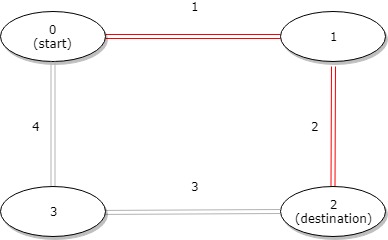
输入：distance = [1,2,3,4], start = 0, destination = 2
输出：3
解释：公交站 0 和 2 之间的距离是 3 或 7，最小值是 3。

 

示例 3：

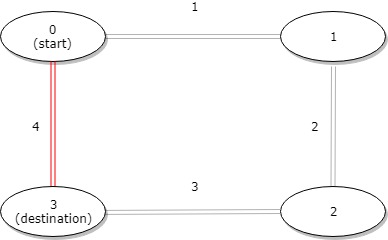
输入：distance = [1,2,3,4], start = 0, destination = 3
输出：4
解释：公交站 0 和 3 之间的距离是 6 或 4，最小值是 4。

 

提示：

• 1 <= n <= 10^4
• distance.length == n
• 0 <= start, destination < n
• 0 <= distance[i] <= 10^4

通过代码

高赞题解

出这么简单的题真的好么……

class Solution {
public:
    int distanceBetweenBusStops(vector<int>& distance, int start, int destination) {
        if(start==destination)return 0;
        if(start>destination)swap(start,destination);

        int n=distance.size();
        int sum1=0;
        int sum2=0;
        for(int i=0;i<start;++i)
        {
            sum2+=distance[i];
        }
        for(int i=start;i<destination;++i)
        {
            sum1+=distance[i];
        }
        for(int i=destination;i<n;++i) 
        {
            sum2+=distance[i];
        }
        return min(sum1,sum2);
    }
};

统计信息

通过次数	提交次数	AC比率
13866	23717	58.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言