原文链接: https://leetcode-cn.com/problems/minimum-cost-to-move-chips-to-the-same-position

英文原文

We have n chips, where the position of the ith chip is position[i].

We need to move all the chips to the same position. In one step, we can change the position of the ith chip from position[i] to:

• position[i] + 2 or position[i] - 2 with cost = 0.
• position[i] + 1 or position[i] - 1 with cost = 1.

Return the minimum cost needed to move all the chips to the same position.

 

Example 1:

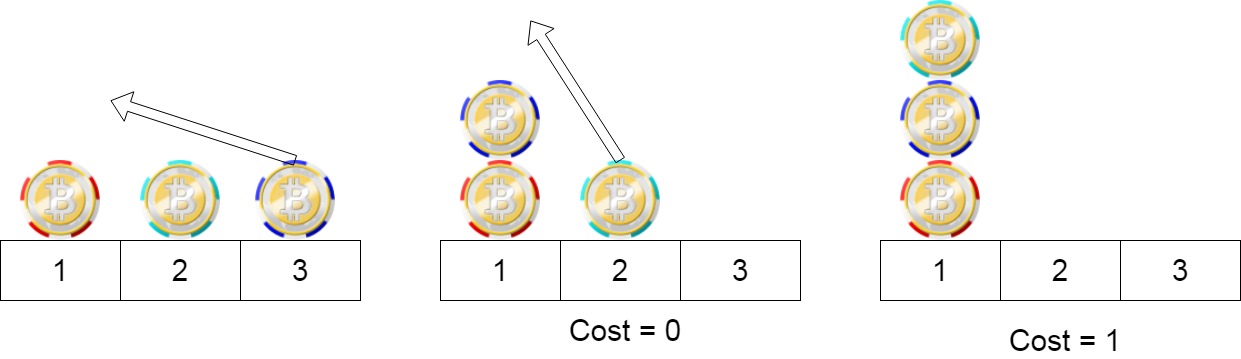
Input: position = [1,2,3]
Output: 1
Explanation: First step: Move the chip at position 3 to position 1 with cost = 0.
Second step: Move the chip at position 2 to position 1 with cost = 1.
Total cost is 1.

Example 2:

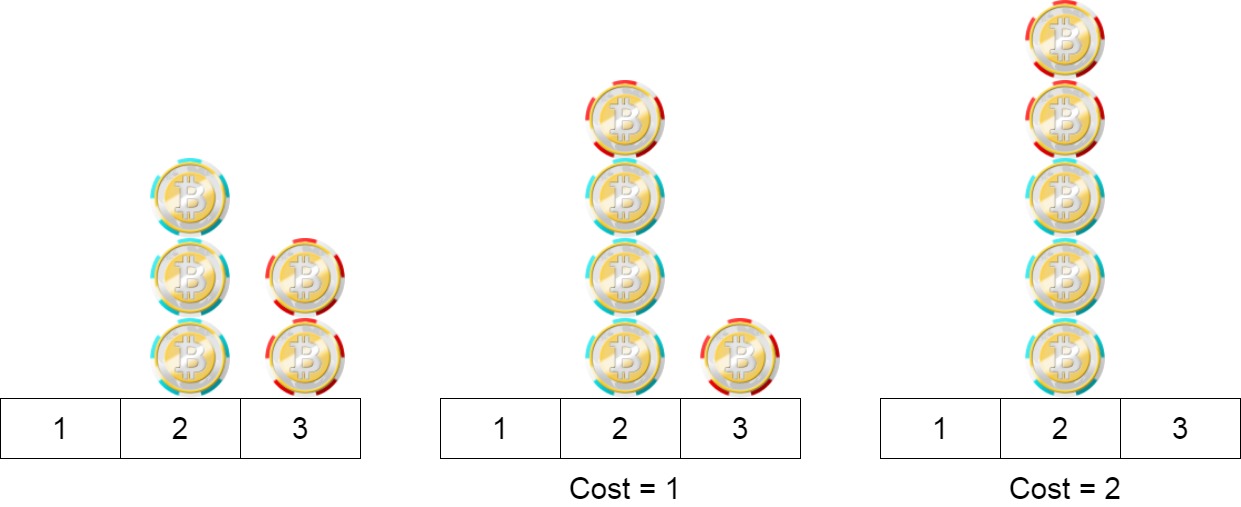
Input: position = [2,2,2,3,3]
Output: 2
Explanation: We can move the two chips at position  3 to position 2. Each move has cost = 1. The total cost = 2.

Example 3:

Input: position = [1,1000000000]
Output: 1

 

Constraints:

• 1 <= position.length <= 100
• 1 <= position[i] <= 10^9

中文题目

数轴上放置了一些筹码，每个筹码的位置存在数组 chips 当中。

你可以对 任何筹码 执行下面两种操作之一（不限操作次数，0 次也可以）：

• 将第 i 个筹码向左或者右移动 2 个单位，代价为 0。
• 将第 i 个筹码向左或者右移动 1 个单位，代价为 1。

最开始的时候，同一位置上也可能放着两个或者更多的筹码。

返回将所有筹码移动到同一位置（任意位置）上所需要的最小代价。

 

示例 1：

输入：chips = [1,2,3]
输出：1
解释：第二个筹码移动到位置三的代价是 1，第一个筹码移动到位置三的代价是 0，总代价为 1。

示例 2：

输入：chips = [2,2,2,3,3]
输出：2
解释：第四和第五个筹码移动到位置二的代价都是 1，所以最小总代价为 2。

 

提示：

• 1 <= chips.length <= 100
• 1 <= chips[i] <= 10^9

通过代码

高赞题解

• 先理解题意：有的人可能理解错题意了，这里的chips数组里存放的是第i个筹码存放的位置，不是第i个位置存放了多少个筹码，这个概念搞清楚了就简单多了。比如chips = [2,2,2,3,3]]表示第1个筹码放第2个位置，第2个筹码放第2个位置，第3个筹码放第2个位置，第4个筹码放第3个位置，第5个筹码放第3个位置，那么这就表示，第2个位置上有3个筹码，第3个位置上有2个筹码，其它位置上没有筹码，可以把第3个位置上的2个筹码移动到第2个位置上，所以代价是2.
• 再理解思路：因为移动2个位置不需要代价，那么奇数位置移到奇数位置不用代价，偶数位置移到偶数位置不用代价，那就分别统计奇数位置和偶数位置的个数，相当于把所有奇数放一起，所有偶数的放一起，然后比较奇数的少还是偶数的少，将少的个数移到多的个数位置上去就可以了。

  public int minCostToMoveChips(int[] chips) {
      int odd = 0, even = 0;
  	for (int i = 0; i < chips.length; i++) {
  		if (chips[i] % 2 == 0) {
  			even++;
  		} else if (chips[i] % 2 != 0) {
  			odd++;
  		}
  	}
  	return Math.min(even, odd);   
      }

统计信息

通过次数	提交次数	AC比率
22660	32585	69.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言