原文链接: https://leetcode-cn.com/problems/minimum-time-visiting-all-points

英文原文

On a 2D plane, there are n points with integer coordinates points[i] = [xi, yi]. Return the minimum time in seconds to visit all the points in the order given by points.

You can move according to these rules:

• In 1 second, you can either:

  <ul>
      <li>move vertically by one&nbsp;unit,</li>
      <li>move horizontally by one unit, or</li>
      <li>move diagonally <code>sqrt(2)</code> units (in other words, move one unit vertically then one unit horizontally in <code>1</code> second).</li>
  </ul>
  </li>
  <li>You have to visit the points in the same order as they appear in the array.</li>
  <li>You are allowed to pass through points that appear later in the order, but these do not count as visits.</li>
  

 

Example 1:

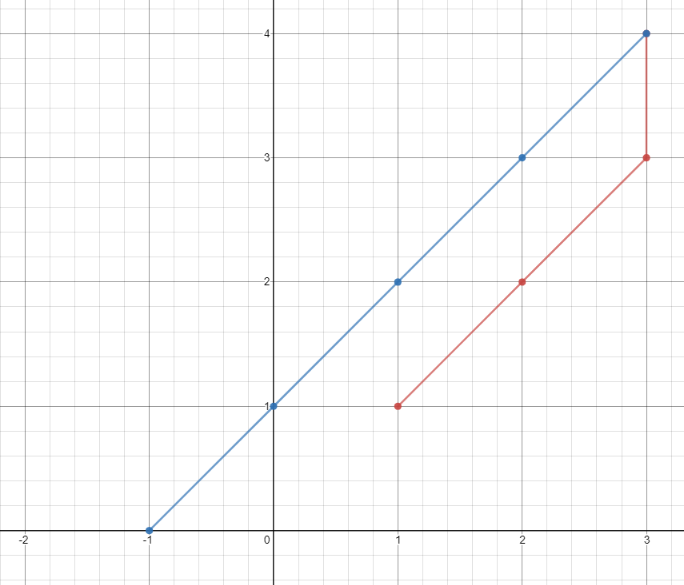
Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]   
Time from [1,1] to [3,4] = 3 seconds 
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds

Example 2:

Input: points = [[3,2],[-2,2]]
Output: 5

 

Constraints:

• points.length == n
• 1 <= n <= 100
• points[i].length == 2
• -1000 <= points[i][0], points[i][1] <= 1000

中文题目

平面上有 n 个点，点的位置用整数坐标表示 points[i] = [xi, yi] 。请你计算访问所有这些点需要的 最小时间（以秒为单位）。

你需要按照下面的规则在平面上移动：

• 每一秒内，你可以：
  • 沿水平方向移动一个单位长度，或者
  • 沿竖直方向移动一个单位长度，或者
  • 跨过对角线移动 sqrt(2) 个单位长度（可以看作在一秒内向水平和竖直方向各移动一个单位长度）。
• 必须按照数组中出现的顺序来访问这些点。
• 在访问某个点时，可以经过该点后面出现的点，但经过的那些点不算作有效访问。

 

示例 1：

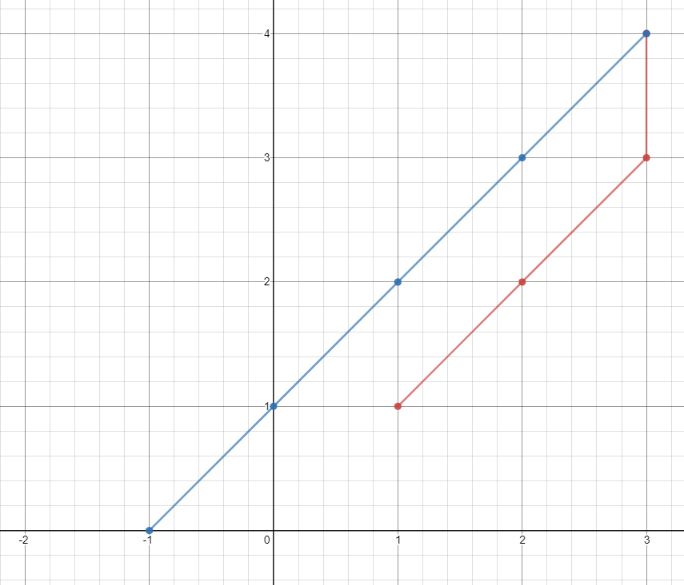
输入：points = [[1,1],[3,4],[-1,0]]
输出：7
解释：一条最佳的访问路径是： [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]   
从 [1,1] 到 [3,4] 需要 3 秒 
从 [3,4] 到 [-1,0] 需要 4 秒
一共需要 7 秒

示例 2：

输入：points = [[3,2],[-2,2]]
输出：5

 

提示：

• points.length == n
• 1 <= n <= 100
• points[i].length == 2
• -1000 <= points[i][0], points[i][1] <= 1000

通过代码

高赞题解

方法一：切比雪夫距离

对于平面上的两个点 x = (x0, x1) 和 y = (y0, y1)，设它们横坐标距离之差为 dx = |x0 - y0|，纵坐标距离之差为 dy = |x1 - y1|，对于以下三种情况，我们可以分别计算出从 x 移动到 y 的最少次数：

• dx < dy：沿对角线移动 dx 次，再竖直移动 dy - dx 次，总计 dx + (dy - dx) = dy 次；

• dx == dy：沿对角线移动 dx 次；

• dx > dy：沿对角线移动 dy 次，再水平移动 dx - dy 次，总计 dy + (dx - dy) = dx 次。

可以发现，对于任意一种情况，从 x 移动到 y 的最少次数为 dx 和 dy 中的较大值 max(dx, dy)，这也被称作 x 和 y 之间的 切比雪夫距离。

由于题目要求，需要按照数组中出现的顺序来访问这些点。因此我们遍历整个数组，对于数组中的相邻两个点，计算出它们的切比雪夫距离，所有的距离之和即为答案。

[sol1]
class Solution {
public:
    int minTimeToVisitAllPoints(vector<vector<int>>& points) {
        int x0 = points[0][0], x1 = points[0][1];
        int ans = 0;
        for (int i = 1; i < points.size(); ++i) {
            int y0 = points[i][0], y1 = points[i][1];
            ans += max(abs(x0 - y0), abs(x1 - y1));
            x0 = y0;
            x1 = y1;
        }
        return ans;
    }
};

[sol1]
class Solution:
    def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:
        x0, x1 = points[0]
        ans = 0
        for i in range(1, len(points)):
            y0, y1 = points[i]
            ans += max(abs(x0 - y0), abs(x1 - y1))
            x0, x1 = points[i]
        return ans

复杂度分析

• 时间复杂度：$O(N)$，其中 $N$ 是数组的长度。

• 空间复杂度：$O(1)$。

统计信息

通过次数	提交次数	AC比率
30358	36825	82.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言