原文链接: https://leetcode-cn.com/problems/find-winner-on-a-tic-tac-toe-game

英文原文

Tic-tac-toe is played by two players A and B on a 3 x 3 grid. The rules of Tic-Tac-Toe are:

• Players take turns placing characters into empty squares ' '.
• The first player A always places 'X' characters, while the second player B always places 'O' characters.
• 'X' and 'O' characters are always placed into empty squares, never on filled ones.
• The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
• The game also ends if all squares are non-empty.
• No more moves can be played if the game is over.

Given a 2D integer array moves where moves[i] = [rowi, coli] indicates that the ith move will be played on grid[rowi][coli]. return the winner of the game if it exists (A or B). In case the game ends in a draw return "Draw". If there are still movements to play return "Pending".

You can assume that moves is valid (i.e., it follows the rules of Tic-Tac-Toe), the grid is initially empty, and A will play first.

 

Example 1:

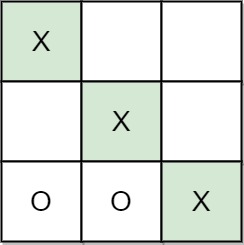
Input: moves = [[0,0],[2,0],[1,1],[2,1],[2,2]]
Output: "A"
Explanation: A wins, they always play first.

Example 2:

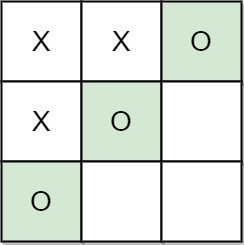
Input: moves = [[0,0],[1,1],[0,1],[0,2],[1,0],[2,0]]
Output: "B"
Explanation: B wins.

Example 3:

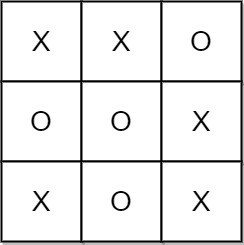
Input: moves = [[0,0],[1,1],[2,0],[1,0],[1,2],[2,1],[0,1],[0,2],[2,2]]
Output: "Draw"
Explanation: The game ends in a draw since there are no moves to make.

Example 4:

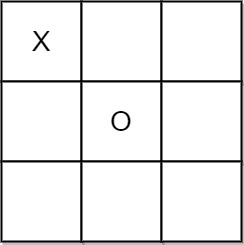
Input: moves = [[0,0],[1,1]]
Output: "Pending"
Explanation: The game has not finished yet.

 

Constraints:

• 1 <= moves.length <= 9
• moves[i].length == 2
• 0 <= rowi, coli <= 2
• There are no repeated elements on moves.
• moves follow the rules of tic tac toe.

中文题目

A 和 B 在一个 3 x 3 的网格上玩井字棋。

井字棋游戏的规则如下：

• 玩家轮流将棋子放在空方格 (" ") 上。
• 第一个玩家 A 总是用 "X" 作为棋子，而第二个玩家 B 总是用 "O" 作为棋子。
• "X" 和 "O" 只能放在空方格中，而不能放在已经被占用的方格上。
• 只要有 3 个相同的（非空）棋子排成一条直线（行、列、对角线）时，游戏结束。
• 如果所有方块都放满棋子（不为空），游戏也会结束。
• 游戏结束后，棋子无法再进行任何移动。

给你一个数组 moves，其中每个元素是大小为 2 的另一个数组（元素分别对应网格的行和列），它按照 A 和 B 的行动顺序（先 A 后 B）记录了两人各自的棋子位置。

如果游戏存在获胜者（A 或 B），就返回该游戏的获胜者；如果游戏以平局结束，则返回 "Draw"；如果仍会有行动（游戏未结束），则返回 "Pending"。

你可以假设 moves 都 有效（遵循井字棋规则），网格最初是空的，A 将先行动。

 

示例 1：

输入：moves = [[0,0],[2,0],[1,1],[2,1],[2,2]]
输出："A"
解释："A" 获胜，他总是先走。
"X  "    "X  "    "X  "    "X  "    "X  "
"   " -> "   " -> " X " -> " X " -> " X "
"   "    "O  "    "O  "    "OO "    "OOX"

示例 2：

输入：moves = [[0,0],[1,1],[0,1],[0,2],[1,0],[2,0]]
输出："B"
解释："B" 获胜。
"X  "    "X  "    "XX "    "XXO"    "XXO"    "XXO"
"   " -> " O " -> " O " -> " O " -> "XO " -> "XO " 
"   "    "   "    "   "    "   "    "   "    "O  "

示例 3：

输入：moves = [[0,0],[1,1],[2,0],[1,0],[1,2],[2,1],[0,1],[0,2],[2,2]]
输出："Draw"
输出：由于没有办法再行动，游戏以平局结束。
"XXO"
"OOX"
"XOX"

示例 4：

输入：moves = [[0,0],[1,1]]
输出："Pending"
解释：游戏还没有结束。
"X  "
" O "
"   "

 

提示：

• 1 <= moves.length <= 9
• moves[i].length == 2
• 0 <= moves[i][j] <= 2
• moves 里没有重复的元素。
• moves 遵循井字棋的规则。

通过代码

高赞题解

1. 题目分析

• 井字棋总共只有$9$个格子，且赢面是固定的
• 可以使用一个$9$位二进制数代表行走的结果，规定：
  • 井字棋坐标$[i,j]$对应于数字的第$3i+j$位
  • 每走一步棋等价于与对应的位进行(异)或运算
• 判断游戏结果的方法：
  • 将一方的数字$num$与赢面对应的数字$k$进行与运算，若结果为$k$，此方获胜
  • 若双方都未获胜：
    • 若总步数为$9$步，则平局($Draw$)
    • 否则，未完成($Pending$)
• (附1)赢面数字：
  • 井字棋的赢面只有$8$种($3$种横+$3$种竖+$2$种对角)
  • 计算举例：${[0,0],[0,1],[0,2]}$为横的一种赢面，对应的$9$位二进制数为$000000111$，即十进制下的$7$
  • 事实上，由对应规则可以得知：
    • $3$种横的赢面数字是公比为$8$的等比数列
    • $3$种竖的赢面数字是公比为$2$的等比数列
    • 总共**只需要计算出$4$个数字($1$种横+$1$种竖+$2$种对角)**，其余按倍数推导即可
  • 所有赢面数字分别为$7, 56(即7\times 8), 448(即7\times 8^2), 73, 146(即73\times 2), 292(即73\times 2^2), 273, 84$
• (附2)我在评论区对使用位运算的思路进行了更细致的阐述，如果有不清楚的地方欢迎移步评论区~

2. Coding

public String tictactoe(int[][] moves) {
    // a, b record the moving results of A, B
    int a = 0, b = 0, len = moves.length;
    // ac records all cases of winning
    int[] ac = {7, 56, 448, 73, 146, 292, 273, 84};
    for(int i = 0; i < len; i ++){
        // if i is add
        if((i & 1) == 1){
            // record the step result
            b ^= 1 << (3 * moves[i][0] + moves[i][1]);
        }
        else {
            a ^= 1 << (3 * moves[i][0] + moves[i][1]);
        }
    }
    for(int i : ac){
        // if the moving result contains the winning case in record, then win
        if((a & i) == i){
            return "A";
        }
        if((b & i) == i){
            return "B";
        }
    }
    // or judge the result by the amount of steps
    return len == 9 ? "Draw" : "Pending";
}

时间复杂度$O(m+n)$，空间复杂度$O(m)$(事实上，此处$m=8,n=9$)

3. 执行结果

统计信息

通过次数	提交次数	AC比率
8450	15504	54.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言