原文链接: https://leetcode-cn.com/problems/longest-common-prefix

英文原文

Write a function to find the longest common prefix string amongst an array of strings.

If there is no common prefix, return an empty string "".

 

Example 1:

Input: strs = ["flower","flow","flight"]
Output: "fl"

Example 2:

Input: strs = ["dog","racecar","car"]
Output: ""
Explanation: There is no common prefix among the input strings.

 

Constraints:

• 1 <= strs.length <= 200
• 0 <= strs[i].length <= 200
• strs[i] consists of only lower-case English letters.

中文题目

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

 

示例 1：

输入：strs = ["flower","flow","flight"]
输出："fl"

示例 2：

输入：strs = ["dog","racecar","car"]
输出：""
解释：输入不存在公共前缀。

 

提示：

• 1 <= strs.length <= 200
• 0 <= strs[i].length <= 200
• strs[i] 仅由小写英文字母组成

通过代码

高赞题解

📺 视频题解

📖 文字题解

方法一：横向扫描

用 $\textit{LCP}(S_1 \ldots S_n)$ 表示字符串 $S_1 \ldots S_n$ 的最长公共前缀。

可以得到以下结论：

$$
\textit{LCP}(S_1 \ldots S_n) = \textit{LCP}(\textit{LCP}(\textit{LCP}(S_1, S_2),S_3),\ldots S_n)
$$

基于该结论，可以得到一种查找字符串数组中的最长公共前缀的简单方法。依次遍历字符串数组中的每个字符串，对于每个遍历到的字符串，更新最长公共前缀，当遍历完所有的字符串以后，即可得到字符串数组中的最长公共前缀。

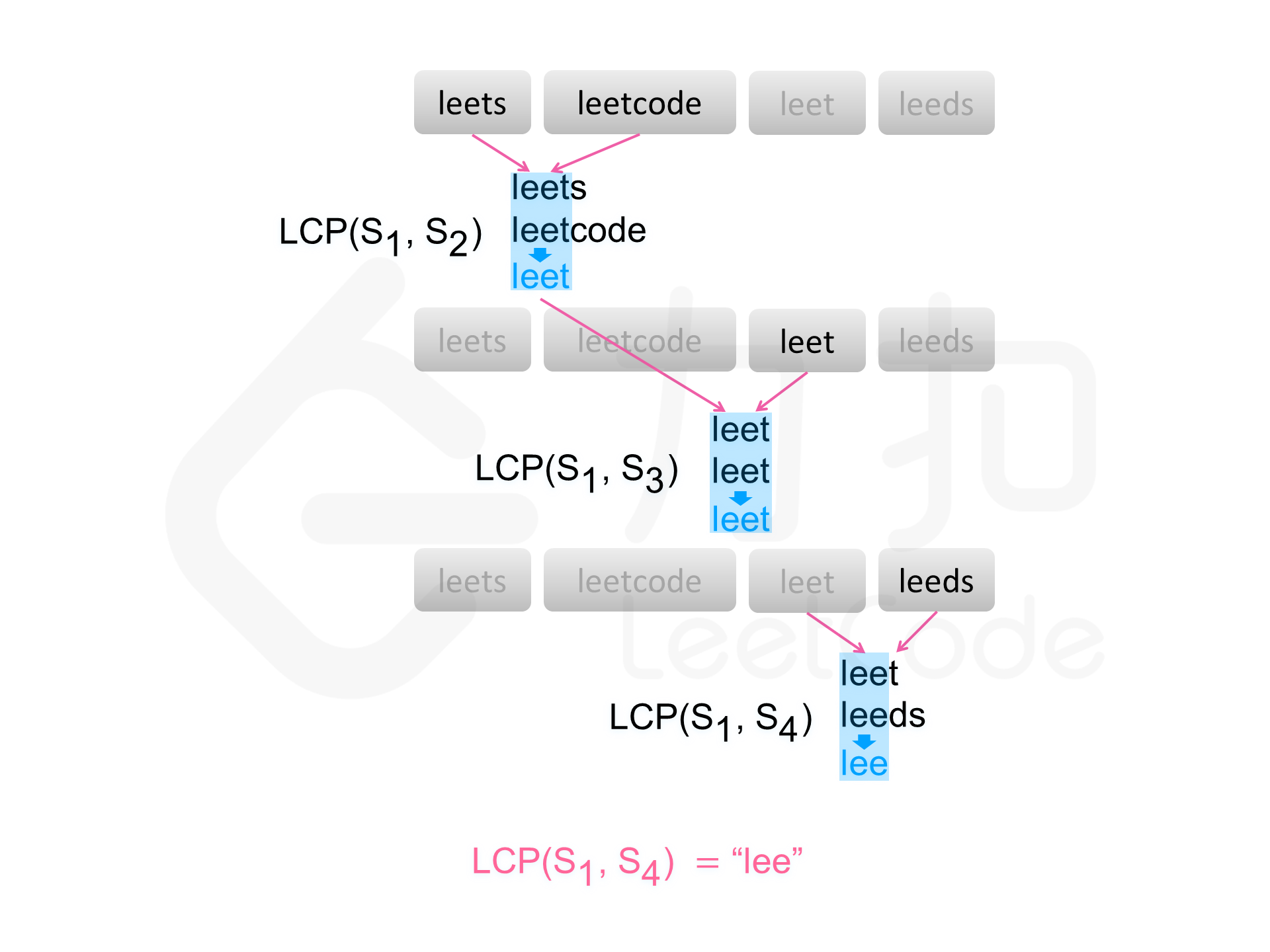{:width=”80%”}

如果在尚未遍历完所有的字符串时，最长公共前缀已经是空串，则最长公共前缀一定是空串，因此不需要继续遍历剩下的字符串，直接返回空串即可。

[sol1-Java]
class Solution {
    public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }
        String prefix = strs[0];
        int count = strs.length;
        for (int i = 1; i < count; i++) {
            prefix = longestCommonPrefix(prefix, strs[i]);
            if (prefix.length() == 0) {
                break;
            }
        }
        return prefix;
    }

    public String longestCommonPrefix(String str1, String str2) {
        int length = Math.min(str1.length(), str2.length());
        int index = 0;
        while (index < length && str1.charAt(index) == str2.charAt(index)) {
            index++;
        }
        return str1.substring(0, index);
    }
}

[sol1-C++]
class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        if (!strs.size()) {
            return "";
        }
        string prefix = strs[0];
        int count = strs.size();
        for (int i = 1; i < count; ++i) {
            prefix = longestCommonPrefix(prefix, strs[i]);
            if (!prefix.size()) {
                break;
            }
        }
        return prefix;
    }

    string longestCommonPrefix(const string& str1, const string& str2) {
        int length = min(str1.size(), str2.size());
        int index = 0;
        while (index < length && str1[index] == str2[index]) {
            ++index;
        }
        return str1.substr(0, index);
    }
};

[sol1-Python3]
class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        if not strs:
            return ""
        
        prefix, count = strs[0], len(strs)
        for i in range(1, count):
            prefix = self.lcp(prefix, strs[i])
            if not prefix:
                break
        
        return prefix

    def lcp(self, str1, str2):
        length, index = min(len(str1), len(str2)), 0
        while index < length and str1[index] == str2[index]:
            index += 1
        return str1[:index]

[sol1-Golang]
func longestCommonPrefix(strs []string) string {
    if len(strs) == 0 {
        return ""
    }
    prefix := strs[0]
    count := len(strs)
    for i := 1; i < count; i++ {
        prefix = lcp(prefix, strs[i])
        if len(prefix) == 0 {
            break
        }
    }
    return prefix
}

func lcp(str1, str2 string) string {
    length := min(len(str1), len(str2))
    index := 0
    for index < length && str1[index] == str2[index] {
        index++
    }
    return str1[:index]
}

func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

复杂度分析

• 时间复杂度：$O(mn)$，其中 $m$ 是字符串数组中的字符串的平均长度，$n$ 是字符串的数量。最坏情况下，字符串数组中的每个字符串的每个字符都会被比较一次。

• 空间复杂度：$O(1)$。使用的额外空间复杂度为常数。

方法二：纵向扫描

方法一是横向扫描，依次遍历每个字符串，更新最长公共前缀。另一种方法是纵向扫描。纵向扫描时，从前往后遍历所有字符串的每一列，比较相同列上的字符是否相同，如果相同则继续对下一列进行比较，如果不相同则当前列不再属于公共前缀，当前列之前的部分为最长公共前缀。

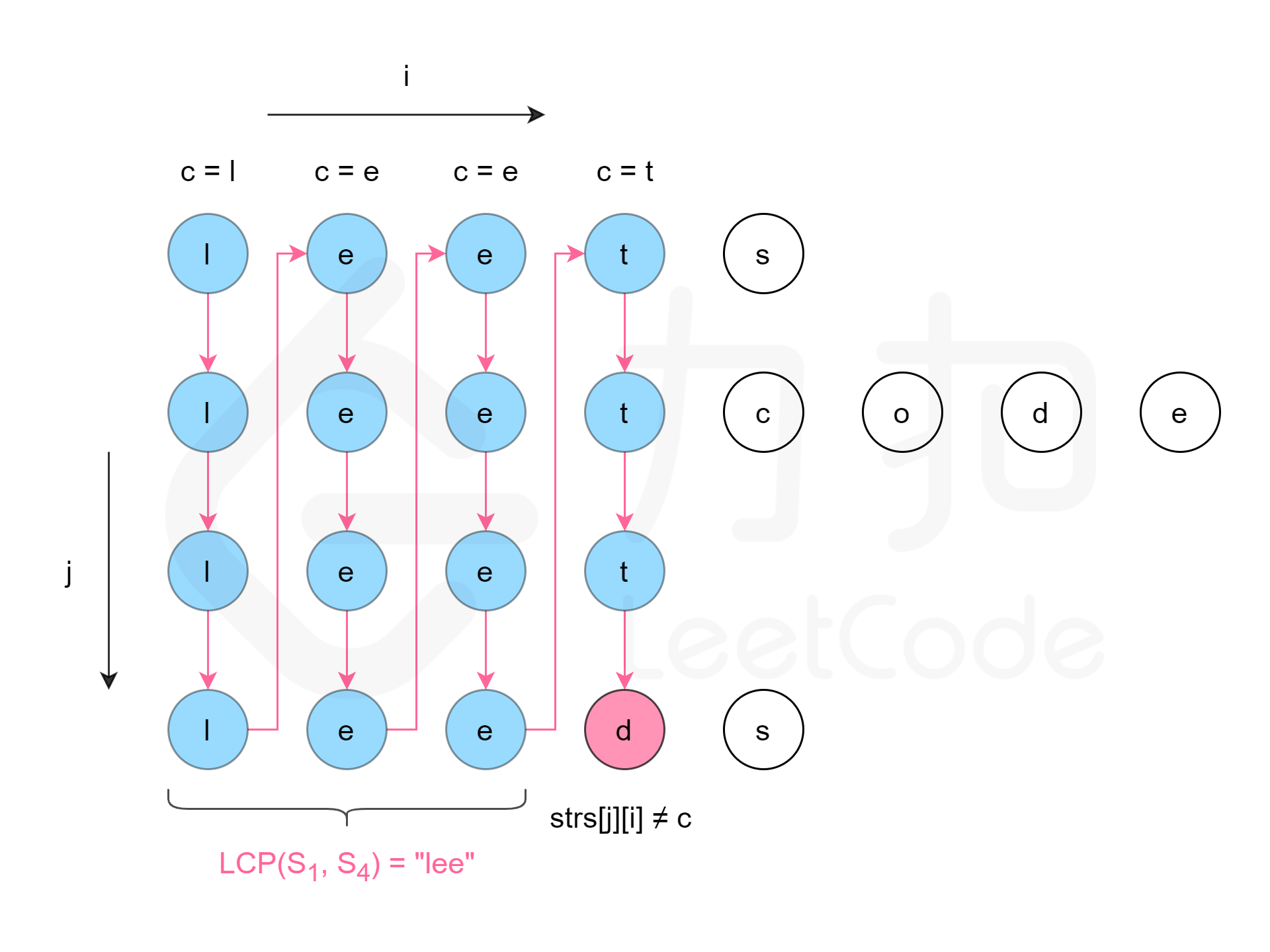{:width=”70%”}

[sol2-Java]
class Solution {
    public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }
        int length = strs[0].length();
        int count = strs.length;
        for (int i = 0; i < length; i++) {
            char c = strs[0].charAt(i);
            for (int j = 1; j < count; j++) {
                if (i == strs[j].length() || strs[j].charAt(i) != c) {
                    return strs[0].substring(0, i);
                }
            }
        }
        return strs[0];
    }
}

[sol2-C++]
class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        if (!strs.size()) {
            return "";
        }
        int length = strs[0].size();
        int count = strs.size();
        for (int i = 0; i < length; ++i) {
            char c = strs[0][i];
            for (int j = 1; j < count; ++j) {
                if (i == strs[j].size() || strs[j][i] != c) {
                    return strs[0].substr(0, i);
                }
            }
        }
        return strs[0];
    }
};

[sol2-Python3]
class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        if not strs:
            return ""
        
        length, count = len(strs[0]), len(strs)
        for i in range(length):
            c = strs[0][i]
            if any(i == len(strs[j]) or strs[j][i] != c for j in range(1, count)):
                return strs[0][:i]
        
        return strs[0]

[sol2-Golang]
func longestCommonPrefix(strs []string) string {
    if len(strs) == 0 {
        return ""
    }
    for i := 0; i < len(strs[0]); i++ {
        for j := 1; j < len(strs); j++ {
            if i == len(strs[j]) || strs[j][i] != strs[0][i] {
                return strs[0][:i]
            }
        }
    }
    return strs[0]
}

复杂度分析

• 时间复杂度：$O(mn)$，其中 $m$ 是字符串数组中的字符串的平均长度，$n$ 是字符串的数量。最坏情况下，字符串数组中的每个字符串的每个字符都会被比较一次。

• 空间复杂度：$O(1)$。使用的额外空间复杂度为常数。

方法三：分治

注意到 $\textit{LCP}$ 的计算满足结合律，有以下结论：

$$
\textit{LCP}(S_1 \ldots S_n) = \textit{LCP}(\textit{LCP}(S_1 \ldots S_k), \textit{LCP} (S_{k+1} \ldots S_n))
$$

其中 $\textit{LCP}(S_1 \ldots S_n)$ 是字符串 $S_1 \ldots S_n$ 的最长公共前缀，$1 < k < n$。

基于上述结论，可以使用分治法得到字符串数组中的最长公共前缀。对于问题 $\textit{LCP}(S_i\cdots S_j)$，可以分解成两个子问题 $\textit{LCP}(S_i \ldots S_{mid})$ 与 $\textit{LCP}(S_{mid+1} \ldots S_j)$，其中 $mid=\frac{i+j}{2}$。对两个子问题分别求解，然后对两个子问题的解计算最长公共前缀，即为原问题的解。

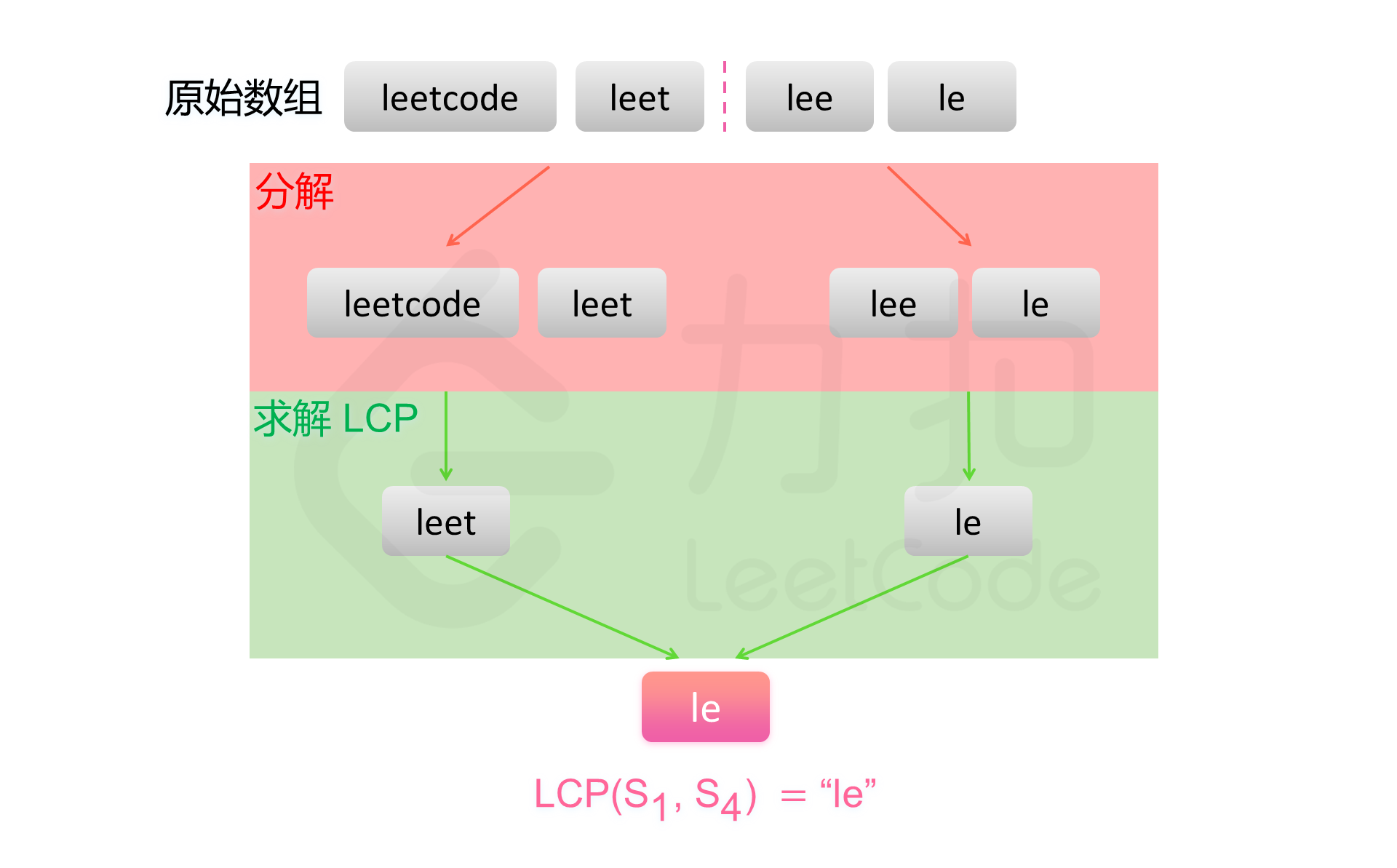{:width=”75%”}

[sol3-Java]
class Solution {
    public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        } else {
            return longestCommonPrefix(strs, 0, strs.length - 1);
        }
    }

    public String longestCommonPrefix(String[] strs, int start, int end) {
        if (start == end) {
            return strs[start];
        } else {
            int mid = (end - start) / 2 + start;
            String lcpLeft = longestCommonPrefix(strs, start, mid);
            String lcpRight = longestCommonPrefix(strs, mid + 1, end);
            return commonPrefix(lcpLeft, lcpRight);
        }
    }

    public String commonPrefix(String lcpLeft, String lcpRight) {
        int minLength = Math.min(lcpLeft.length(), lcpRight.length());       
        for (int i = 0; i < minLength; i++) {
            if (lcpLeft.charAt(i) != lcpRight.charAt(i)) {
                return lcpLeft.substring(0, i);
            }
        }
        return lcpLeft.substring(0, minLength);
    }
}

[sol3-C++]
class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        if (!strs.size()) {
            return "";
        }
        else {
            return longestCommonPrefix(strs, 0, strs.size() - 1);
        }
    }

    string longestCommonPrefix(const vector<string>& strs, int start, int end) {
        if (start == end) {
            return strs[start];
        }
        else {
            int mid = (start + end) / 2;
            string lcpLeft = longestCommonPrefix(strs, start, mid);
            string lcpRight = longestCommonPrefix(strs, mid + 1, end);
            return commonPrefix(lcpLeft, lcpRight);
        }
    }

    string commonPrefix(const string& lcpLeft, const string& lcpRight) {
        int minLength = min(lcpLeft.size(), lcpRight.size());
        for (int i = 0; i < minLength; ++i) {
            if (lcpLeft[i] != lcpRight[i]) {
                return lcpLeft.substr(0, i);
            }
        }
        return lcpLeft.substr(0, minLength);
    }
};

[sol3-Python3]
class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        def lcp(start, end):
            if start == end:
                return strs[start]

            mid = (start + end) // 2
            lcpLeft, lcpRight = lcp(start, mid), lcp(mid + 1, end)
            minLength = min(len(lcpLeft), len(lcpRight))
            for i in range(minLength):
                if lcpLeft[i] != lcpRight[i]:
                    return lcpLeft[:i]

            return lcpLeft[:minLength]

        return "" if not strs else lcp(0, len(strs) - 1)

[sol3-Golang]
func longestCommonPrefix(strs []string) string {
    if len(strs) == 0 {
        return ""
    }
    var lcp func(int, int) string
    lcp = func(start, end int) string {
        if start == end {
            return strs[start]
        }
        mid := (start + end) / 2
        lcpLeft, lcpRight := lcp(start, mid), lcp(mid + 1, end)
        minLength := min(len(lcpLeft), len(lcpRight))
        for i := 0; i < minLength; i++ {
            if lcpLeft[i] != lcpRight[i] {
                return lcpLeft[:i]
            }
        }
        return lcpLeft[:minLength]
    }
    return lcp(0, len(strs)-1)
}

func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

复杂度分析

• 时间复杂度：$O(mn)$，其中 $m$ 是字符串数组中的字符串的平均长度，$n$ 是字符串的数量。时间复杂度的递推式是 $T(n)=2 \cdot T(\frac{n}{2})+O(m)$，通过计算可得 $T(n)=O(mn)$。

• 空间复杂度：$O(m \log n)$，其中 $m$ 是字符串数组中的字符串的平均长度，$n$ 是字符串的数量。空间复杂度主要取决于递归调用的层数，层数最大为 $\log n$，每层需要 $m$ 的空间存储返回结果。

方法四：二分查找

显然，最长公共前缀的长度不会超过字符串数组中的最短字符串的长度。用 $\textit{minLength}$ 表示字符串数组中的最短字符串的长度，则可以在 $[0,\textit{minLength}]$ 的范围内通过二分查找得到最长公共前缀的长度。每次取查找范围的中间值 $\textit{mid}$，判断每个字符串的长度为 $\textit{mid}$ 的前缀是否相同，如果相同则最长公共前缀的长度一定大于或等于 $\textit{mid}$，如果不相同则最长公共前缀的长度一定小于 $\textit{mid}$，通过上述方式将查找范围缩小一半，直到得到最长公共前缀的长度。

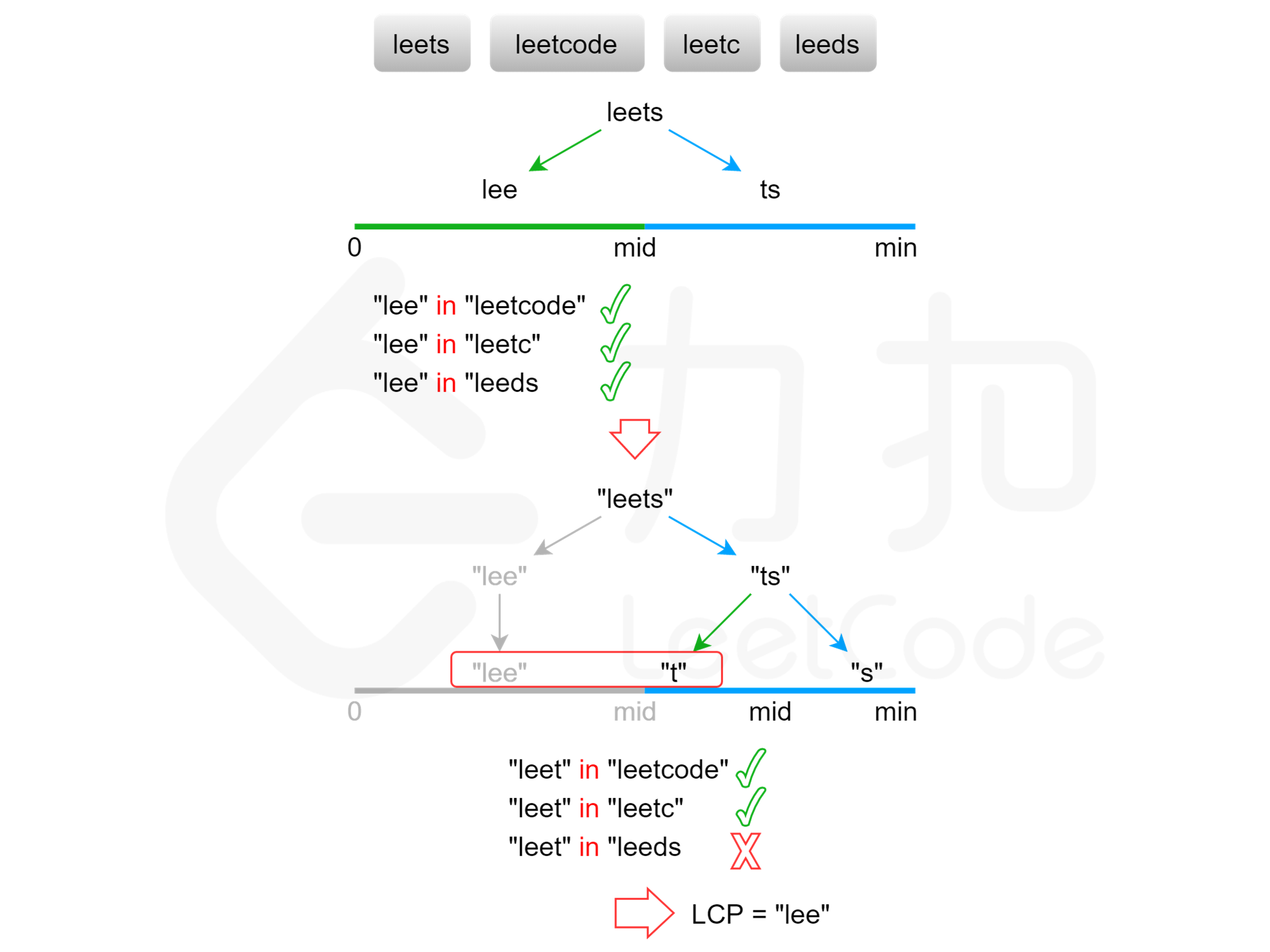{:width=”80%”}

[sol4-Java]
class Solution {
    public String longestCommonPrefix(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }
        int minLength = Integer.MAX_VALUE;
        for (String str : strs) {
            minLength = Math.min(minLength, str.length());
        }
        int low = 0, high = minLength;
        while (low < high) {
            int mid = (high - low + 1) / 2 + low;
            if (isCommonPrefix(strs, mid)) {
                low = mid;
            } else {
                high = mid - 1;
            }
        }
        return strs[0].substring(0, low);
    }

    public boolean isCommonPrefix(String[] strs, int length) {
        String str0 = strs[0].substring(0, length);
        int count = strs.length;
        for (int i = 1; i < count; i++) {
            String str = strs[i];
            for (int j = 0; j < length; j++) {
                if (str0.charAt(j) != str.charAt(j)) {
                    return false;
                }
            }
        }
        return true;
    }
}

[sol4-C++]
class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        if (!strs.size()) {
            return "";
        }
        int minLength = min_element(strs.begin(), strs.end(), [](const string& s, const string& t) {return s.size() < t.size();})->size();
        int low = 0, high = minLength;
        while (low < high) {
            int mid = (high - low + 1) / 2 + low;
            if (isCommonPrefix(strs, mid)) {
                low = mid;
            }
            else {
                high = mid - 1;
            }
        }
        return strs[0].substr(0, low);
    }

    bool isCommonPrefix(const vector<string>& strs, int length) {
        string str0 = strs[0].substr(0, length);
        int count = strs.size();
        for (int i = 1; i < count; ++i) {
            string str = strs[i];
            for (int j = 0; j < length; ++j) {
                if (str0[j] != str[j]) {
                    return false;
                }
            }
        }
        return true;
    }
};

[sol4-Python3]
class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        def isCommonPrefix(length):
            str0, count = strs[0][:length], len(strs)
            return all(strs[i][:length] == str0 for i in range(1, count))

        if not strs:
            return ""

        minLength = min(len(s) for s in strs)
        low, high = 0, minLength
        while low < high:
            mid = (high - low + 1) // 2 + low
            if isCommonPrefix(mid):
                low = mid
            else:
                high = mid - 1

        return strs[0][:low]

[sol4-Golang]
func longestCommonPrefix(strs []string) string {
    if len(strs) == 0 {
        return ""
    }

    isCommonPrefix := func(length int) bool {
        str0, count := strs[0][:length], len(strs)
        for i := 1; i < count; i++ {
            if strs[i][:length] != str0 {
                return false
            }
        }
        return true
    }
    minLength := len(strs[0])
    for _, s := range strs {
        if len(s) < minLength {
            minLength = len(s)
        }
    }
    low, high := 0, minLength
    for low < high {
        mid := (high - low + 1) / 2 + low
        if isCommonPrefix(mid) {
            low = mid
        } else {
            high = mid - 1
        }
    }
    return strs[0][:low]
}

复杂度分析

• 时间复杂度：$O(mn \log m)$，其中 $m$ 是字符串数组中的字符串的最小长度，$n$ 是字符串的数量。二分查找的迭代执行次数是 $O(\log m)$，每次迭代最多需要比较 $mn$ 个字符，因此总时间复杂度是 $O(mn \log m)$。

• 空间复杂度：$O(1)$。使用的额外空间复杂度为常数。

统计信息

通过次数	提交次数	AC比率
673094	1629313	41.3%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言