原文链接: https://leetcode-cn.com/problems/path-crossing

英文原文

Given a string path, where path[i] = 'N', 'S', 'E' or 'W', each representing moving one unit north, south, east, or west, respectively. You start at the origin (0, 0) on a 2D plane and walk on the path specified by path.

Return true if the path crosses itself at any point, that is, if at any time you are on a location you have previously visited. Return false otherwise.

 

Example 1:

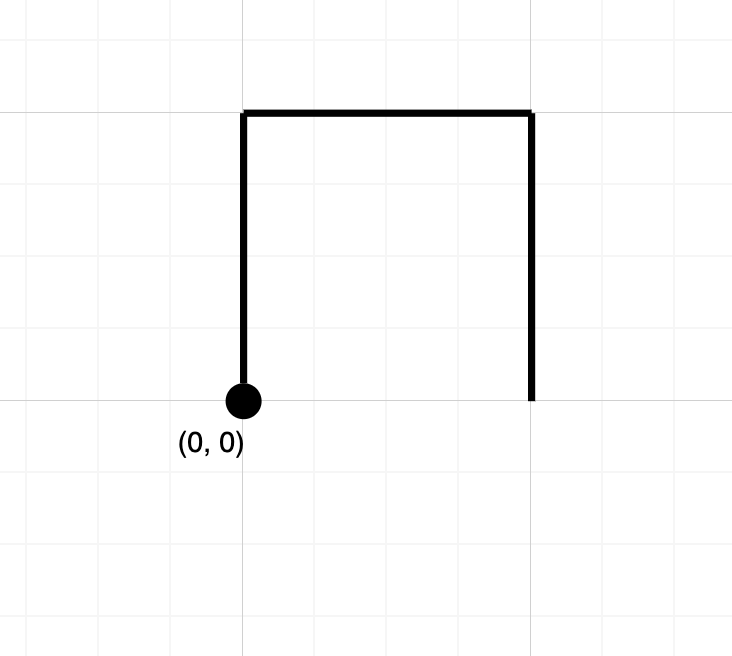
Input: path = "NES"
Output: false 
Explanation: Notice that the path doesn't cross any point more than once.

Example 2:

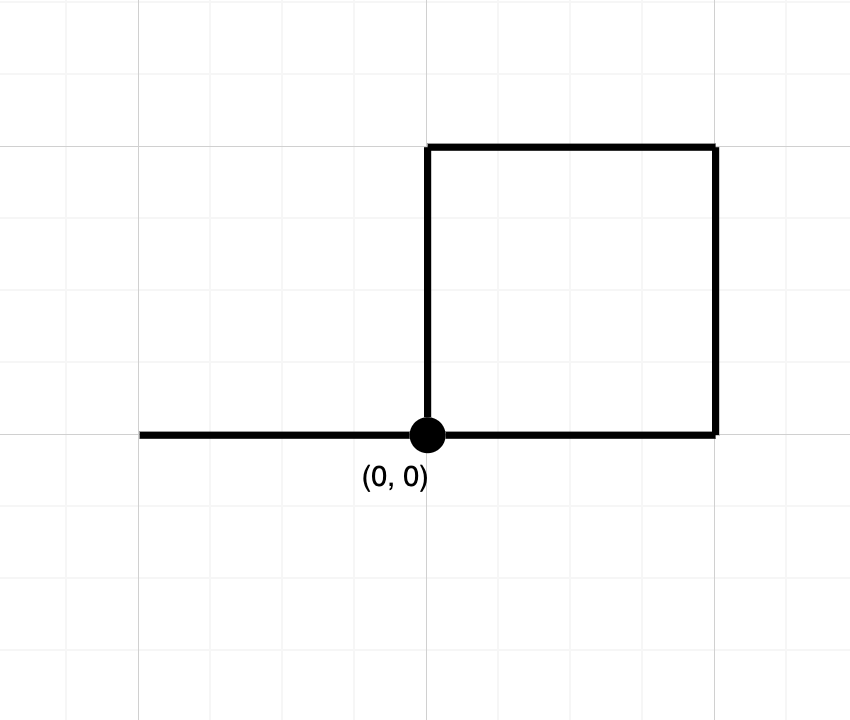
Input: path = "NESWW"
Output: true
Explanation: Notice that the path visits the origin twice.

 

Constraints:

• 1 <= path.length <= 104
• path[i] is either 'N', 'S', 'E', or 'W'.

中文题目

给你一个字符串 path，其中 path[i] 的值可以是 'N'、'S'、'E' 或者 'W'，分别表示向北、向南、向东、向西移动一个单位。

机器人从二维平面上的原点 (0, 0) 处开始出发，按 path 所指示的路径行走。

如果路径在任何位置上出现相交的情况，也就是走到之前已经走过的位置，请返回 True ；否则，返回 False 。

 

示例 1：

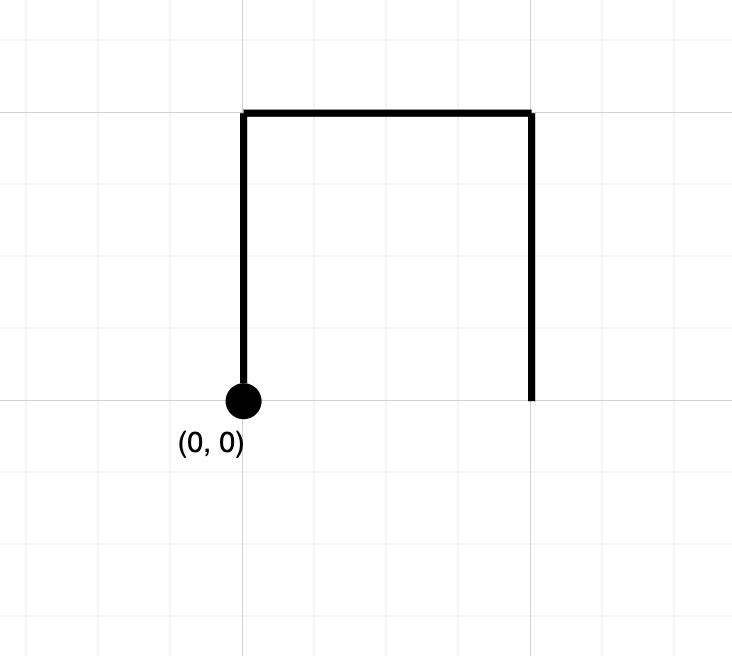
输入：path = "NES"
输出：false 
解释：该路径没有在任何位置相交。

示例 2：

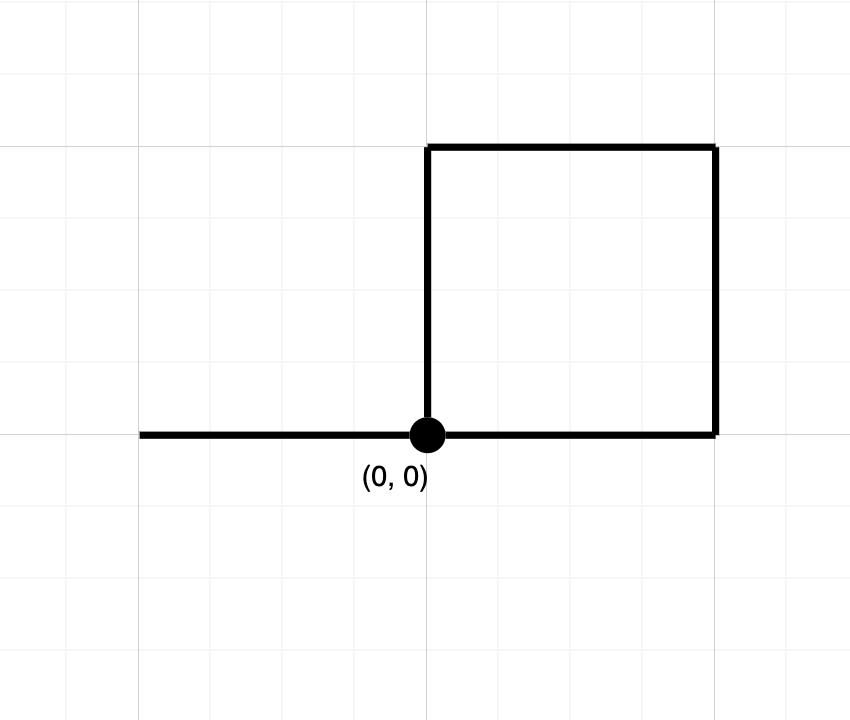
输入：path = "NESWW"
输出：true
解释：该路径经过原点两次。

 

提示：

• 1 <= path.length <= 10^4
• path 仅由 {'N', 'S', 'E', 'W} 中的字符组成

通过代码

高赞题解

方法一：哈希表

思路

我们可以模拟机器人行走的过程，机器人行走的本质是它的坐标发生了变化，要解决这个问题，就要保存机器人走过的所有坐标——所以这道题的关键在于如何判断「走到之前已经走过的位置」。

由于数组 $\it path$ 的长度最大是 $10^4$，我们并不能开一个二维数组来表示这个坐标平面：在极端情况下，机器人每次都沿着同一个方向前进，开二维数组需要 $(10^4)^2$ 个布尔类型变量的空间，它非常大。实际上，这 $(10^4)^2$ 个位置并不是都能用到，大多数位置是没有访问到的，用这样的方法打访问标记会造成很大的空间浪费。

因此我们可以用哈希表来解决这个问题，即我们可以给「已经走过」的位置打上访问标记，把坐标 $(x, y)$ 存入哈希表，每次模拟坐标的变化得到新的坐标，在哈希表中查询这个坐标对应的哈希值有没有出现过，这样既不用花费很大的空间，又能快速查询到一个坐标是否访问过。

在 C++ 语言中，如果使用 pair<int, int> 存储坐标，那么我们需要自己实现哈希映射函数。我们可以令哈希函数 $f(x, y) = x \times 20001 + y$，这是因为 $y$ 的取值范围在 $[-10^4, 10^4]$ 内，共有 $20001$ 种可能性，上述的哈希函数就不会造成冲突。在 Python 语言中，我们使用元组 tuple 存储坐标，可以直接放入哈希表 set 中。

代码如下。

代码

[sol1-C++]
class Solution {
public:
    int getHash(int x, int y) {
        return x * 20001 + y;
    }

    bool isPathCrossing(string path) {
        unordered_set<int> vis;

        int x = 0, y = 0;
        vis.insert(getHash(x, y));

        for (char dir: path) {
            switch (dir) {
                case 'N': --x; break;
                case 'S': ++x; break;
                case 'W': --y; break;
                case 'E': ++y; break;
            }
            int hashValue = getHash(x, y);
            if (vis.find(hashValue) != vis.end()) {
                return true;
            } else {
                vis.insert(hashValue);
            }
        }

        return false;
    }
};

[sol1-C++11]
class Solution {
public:
    bool isPathCrossing(string path) {
        auto pairHash = [](const pair<int, int>& o) {
            return o.first * 20001 + o.second;
        };
        unordered_set<pair<int, int>, decltype(pairHash)> vis(0, pairHash);

        int x = 0, y = 0;
        vis.emplace(x, y);

        for (char dir: path) {
            switch (dir) {
                case 'N': --x; break;
                case 'S': ++x; break;
                case 'W': --y; break;
                case 'E': ++y; break;
            }
            if (vis.find({x, y}) != vis.end()) {
                return true;
            } else {
                vis.emplace(x, y);
            }
        }

        return false;
    }
};

[sol1-Java]
class Solution {
    public boolean isPathCrossing(String path) {
        Set<Integer> vis = new HashSet<Integer>();

        int x = 0, y = 0;
        vis.add(getHash(x, y));

        int length = path.length();
        for (int i = 0; i < length; i++) {
            char dir = path.charAt(i);
            switch (dir) {
                case 'N': --x; break;
                case 'S': ++x; break;
                case 'W': --y; break;
                case 'E': ++y; break;
            }
            int hashValue = getHash(x, y);
            if (!vis.add(hashValue)) {
                return true;
            }
        }

        return false;
    }

    public int getHash(int x, int y) {
        return x * 20001 + y;
    }
}

[sol1-Python3]
class Solution:
    def isPathCrossing(self, path: str) -> bool:
        dirs = {
            "N": (-1, 0),
            "S": (1, 0),
            "W": (0, -1),
            "E": (0, 1),
        }
        
        x, y = 0, 0
        vis = set([(x, y)])
        for ch in path:
            dx, dy = dirs[ch]
            x, y = x + dx, y + dy
            if (x, y) in vis:
                return True
            vis.add((x, y))

        return False

复杂度

假设 path 的长度为 $n$。

• 时间复杂度：$O(n)$。最坏情况下，对于 $n$ 个元素，每个元素做一次 $O(1)$ 的哈希表查询和一次 $O(1)$ 的哈希表插入。

• 空间复杂度：$O(n)$。这里使用了哈希表作为辅助空间，故空间代价是 $O(n)$。

统计信息

通过次数	提交次数	AC比率
11471	21384	53.6%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言