原文链接: https://leetcode-cn.com/problems/most-visited-sector-in-a-circular-track
英文原文
Given an integer n and an integer array rounds. We have a circular track which consists of n sectors labeled from 1 to n. A marathon will be held on this track, the marathon consists of m rounds. The ith round starts at sector rounds[i - 1] and ends at sector rounds[i]. For example, round 1 starts at sector rounds[0] and ends at sector rounds[1]
Return an array of the most visited sectors sorted in ascending order.
Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).
Example 1:
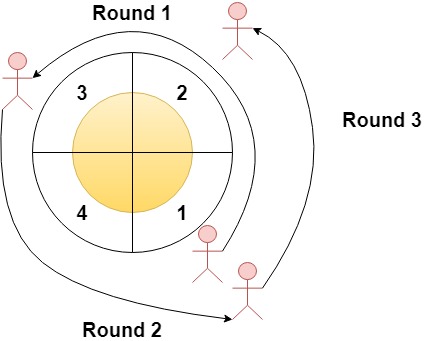
Input: n = 4, rounds = [1,3,1,2] Output: [1,2] Explanation: The marathon starts at sector 1. The order of the visited sectors is as follows: 1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon) We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.
Example 2:
Input: n = 2, rounds = [2,1,2,1,2,1,2,1,2] Output: [2]
Example 3:
Input: n = 7, rounds = [1,3,5,7] Output: [1,2,3,4,5,6,7]
Constraints:
2 <= n <= 1001 <= m <= 100rounds.length == m + 11 <= rounds[i] <= nrounds[i] != rounds[i + 1]for0 <= i < m
中文题目
给你一个整数 n 和一个整数数组 rounds 。有一条圆形赛道由 n 个扇区组成,扇区编号从 1 到 n 。现将在这条赛道上举办一场马拉松比赛,该马拉松全程由 m 个阶段组成。其中,第 i 个阶段将会从扇区 rounds[i - 1] 开始,到扇区 rounds[i] 结束。举例来说,第 1 阶段从 rounds[0] 开始,到 rounds[1] 结束。
请你以数组形式返回经过次数最多的那几个扇区,按扇区编号 升序 排列。
注意,赛道按扇区编号升序逆时针形成一个圆(请参见第一个示例)。
示例 1:
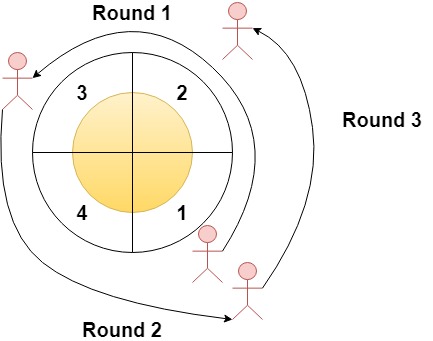
输入:n = 4, rounds = [1,3,1,2] 输出:[1,2] 解释:本场马拉松比赛从扇区 1 开始。经过各个扇区的次序如下所示: 1 --> 2 --> 3(阶段 1 结束)--> 4 --> 1(阶段 2 结束)--> 2(阶段 3 结束,即本场马拉松结束) 其中,扇区 1 和 2 都经过了两次,它们是经过次数最多的两个扇区。扇区 3 和 4 都只经过了一次。
示例 2:
输入:n = 2, rounds = [2,1,2,1,2,1,2,1,2] 输出:[2]
示例 3:
输入:n = 7, rounds = [1,3,5,7] 输出:[1,2,3,4,5,6,7]
提示:
2 <= n <= 1001 <= m <= 100rounds.length == m + 11 <= rounds[i] <= nrounds[i] != rounds[i + 1],其中0 <= i < m
通过代码
高赞题解
[5495] 圆形赛道上经过次数最多的扇区
题目思考
- 如何简化问题?
解决方案
思路
- 题目 blahblah 说了很长, 但仔细分析可以发现, 中间部分对结果完全没影响, 中间不管有多少个值多少圈, 对于每个扇区增加的次数都是相同的
- 所以我们可以只考虑起点和终点, 简化为一圈的情况, 这一圈经过的扇区是额外的部分, 最终结果只需要考虑起点和终点途径的扇区即可
- 注意终点可能小于起点, 这时候就要先从 1 到终点, 再从起点遍历到 n 即可(因为最终结果要按顺序)
复杂度
- 时间复杂度
O(N): 只需要遍历起点和终点之间的部分 - 空间复杂度
O(1): 只使用了几个变量
代码
class Solution:
def mostVisited(self, n: int, rounds: List[int]) -> List[int]:
s, e = rounds[0], rounds[-1]
if s <= e:
# [起点, 终点]
return list(range(s, e + 1))
else:
# [1, 终点]+[起点, n]
return list(range(1, e + 1)) + list(range(s, n + 1))[5496] 你可以获得的最大硬币数目
题目思考
- 如何保证自己每次拿到的都是最优的?
解决方案
思路
- 贪心法, 既然我们只能拿第二大的, 那每次都把最大的留给 Alice, 然后我们选第二大的, 再把当前最小的塞给 Bob 就行了
- 转换成代码就是先排序, 然后从大到小遍历, 从第二大的开始拿, 每次中间隔一个值(把当前最大的留给 Alice), 直到我们拿够 n 个硬币 (总共 3n 个硬币)
复杂度
- 时间复杂度
O(NlogN): 需要排序 - 空间复杂度
O(1): 只使用了几个变量
代码
class Solution:
def maxCoins(self, piles: List[int]) -> int:
piles.sort()
cnt = 0
res = 0
for i in range(len(piles) - 2, -1, -2):
# 从次大值开始, 隔一个硬币拿一次
res += piles[i]
cnt += 1
if cnt == len(piles) // 3:
break
return res[5497] 查找大小为 M 的最新分组
题目思考
- 需要哪些数据结构?
- 当前位置变成 1 之后会改变哪些位置的连续 1 的长度?
解决方案
思路
- 分析题目, 某个位置变成 1 之后, 最直接的影响就是其左右两边, 左右两边连续的 1 的长度都会变成新的总长度
- 所以首先我们需要一个字典 iToLen, 键值对为
{i:len}, 存储某个下标对应的连续 1 的长度, 用于动态更新 - 其次我们还需要一个反向字典 lenToCnt, 键值对为
{len:cnt}, 存储当前连续 1 长度对应的个数, 那么每次只要这个字典里 m 对应的 cnt 大于 0, 就说明仍有连续 1 长度为 m 的部分 - 如果我们在每次把某个位置变成 1 之后都修改左右两边所有连续 1 的位置的 iToLen 字典, 这样时间复杂度就达到了 O(N^2), 大概率会超时
- 但真的有必要修改所有下标吗? 答案是否定的, 其实我们只需要修改新的连续 1 的起点和终点的 iToLen 字典即可, 因为后面操作里新的 1 的左右两边绝不可能是当前连续 1 的中间部分, 只需要考虑两个边界就行, 这样就把这部分操作从 O(N)降到了 O(1)
- 然后就是修改反向字典 lenToCnt 了, 这个也很简单, 就是拿到原来左右两侧连续 1 的长度 left 和 right, 将其对应的值各减去 left 和 right, 因为这些下标的长度都不再是原来的值了, 然后再把总长度 left+right+1 在 lenToCnt 字典中的值加上 left+right+1 即可
- 下面代码对必要的步骤有详细的解释, 方便大家理解
复杂度
- 时间复杂度
O(N): 只遍历了数组一遍 - 空间复杂度
O(N): 使用了额外两个字典, 需要存 N 个元素
代码
class Solution:
def findLatestStep(self, arr: List[int], m: int) -> int:
n = len(arr)
lenToCnt = collections.defaultdict(int)
iToLen = {}
res = -1
for index, x in enumerate(arr):
# 转成以0为起点的下标
i = x - 1
# 原来的左侧和右侧的连续1的长度
left = 0
right = 0
# 新的连续1的起点和终点下标, 初始化为当前下标
start = i
end = i
if i - 1 >= 0 and i - 1 in iToLen:
# 更新左侧长度和起点下标
left = iToLen[i - 1]
start -= left
if i + 1 < n and i + 1 in iToLen:
# 更新右侧长度和终点下标
right = iToLen[i + 1]
end += right
newlen = left + right + 1
# 更新iToLen字典, 只需要更新两个边界即可
iToLen[start] = newlen
iToLen[end] = newlen
# 更新lenToCnt字典, 减去旧长度的值, 加上新长度的值
lenToCnt[left] -= left
lenToCnt[right] -= right
lenToCnt[newlen] += newlen
if lenToCnt[m] > 0:
# 如果仍有连续1长度为m的部分, 更新最终结果为当前arr下标+1
res = index + 1
return res[5498] 石子游戏 V
题目思考
- 如何避免重复计算?
解决方案
思路
- 一般对于这种博弈问题, 都可以先尝试用记忆化搜索的思路来解决, 这个题也不例外
- 但这道题不需要双方做最优决策, 只需要 Alice 一个人来分, 所以不需要额外一个 flag 来判断当前是谁的回合
- 直接模拟整个过程, 传入当前元组(转成元组的目的是可以作为 memo 字典的 key), 然后依次遍历当前元组, 动态求得左侧和右侧部分的和, 根据题目描述的情况继续递归, 最终求得最大值作为当前元组的最终结果, 加入 memo 字典中
- 递归出口是元组长度为 1 的时候, 此时游戏结束, 直接返回 0 即可
- 下面代码对必要的步骤有详细的解释, 方便大家理解
复杂度
- 时间复杂度
O(N^3): memo 字典中最多存 N^2 个状态(对应长度为 2~N 的元组, 长度为 2 时有 N-1 个元组, 为 N 时有 1 个, 所以前 N-1 项和就是 N^2 数量级), 然后每次递归的时候需要遍历 N 个数 - 空间复杂度
O(N^2): memo 字典需要存2*N个状态
代码
class Solution:
def stoneGameV(self, stoneValue: List[int]) -> int:
# 记忆化搜索
memo = {}
def getMx(t):
if len(t) == 1:
# 递归出口, 只有1个石头, 返回0
return 0
# 用memo字典存当前元组下的最大值, 避免重复计算
if t not in memo:
# 先计算当前的总和
sm = sum(t)
# 记录左侧行的当前和
leftsm = 0
mx = 0
for i in range(len(t) - 1):
leftsm += t[i]
# 根据总和以及当前左侧和得到右侧和
rightsm = sm - leftsm
# 模拟题目的三种情况, 求不同分片下的最大值, 作为当前元组的最终结果
if leftsm < rightsm:
mx = max(mx, leftsm + getMx(t[:i + 1]))
elif leftsm == rightsm:
mx = max(mx, leftsm + getMx(t[:i + 1]),
leftsm + getMx(t[i + 1:]))
else:
mx = max(mx, rightsm + getMx(t[i + 1:]))
memo[t] = mx
return memo[t]
return getMx(tuple(stoneValue))统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 8905 | 15561 | 57.2% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




