原文链接: https://leetcode-cn.com/problems/design-an-ordered-stream

英文原文

There is a stream of n (idKey, value) pairs arriving in an arbitrary order, where idKey is an integer between 1 and n and value is a string. No two pairs have the same id.

Design a stream that returns the values in increasing order of their IDs by returning a chunk (list) of values after each insertion. The concatenation of all the chunks should result in a list of the sorted values.

Implement the OrderedStream class:

• OrderedStream(int n) Constructs the stream to take n values.
• String[] insert(int idKey, String value) Inserts the pair (idKey, value) into the stream, then returns the largest possible chunk of currently inserted values that appear next in the order.

 

Example:

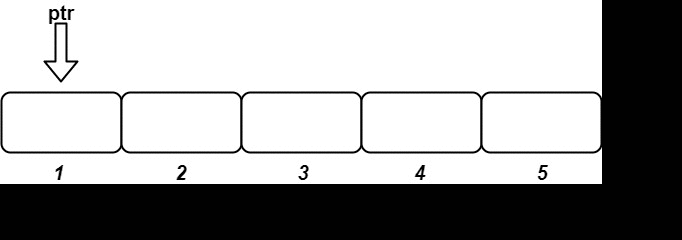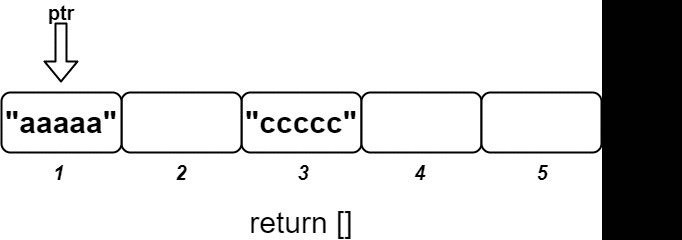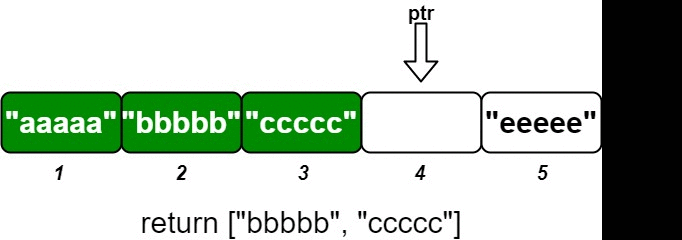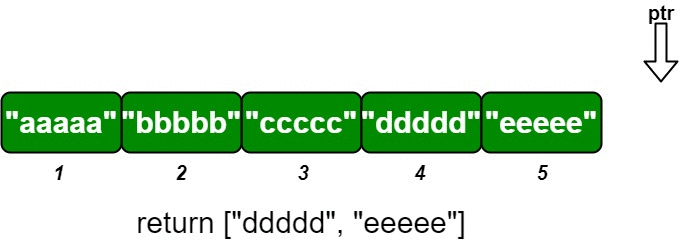
Input
["OrderedStream", "insert", "insert", "insert", "insert", "insert"]
[[5], [3, "ccccc"], [1, "aaaaa"], [2, "bbbbb"], [5, "eeeee"], [4, "ddddd"]]
Output
[null, [], ["aaaaa"], ["bbbbb", "ccccc"], [], ["ddddd", "eeeee"]]

Explanation
// Note that the values ordered by ID is ["aaaaa", "bbbbb", "ccccc", "ddddd", "eeeee"].
OrderedStream os = new OrderedStream(5);
os.insert(3, "ccccc"); // Inserts (3, "ccccc"), returns [].
os.insert(1, "aaaaa"); // Inserts (1, "aaaaa"), returns ["aaaaa"].
os.insert(2, "bbbbb"); // Inserts (2, "bbbbb"), returns ["bbbbb", "ccccc"].
os.insert(5, "eeeee"); // Inserts (5, "eeeee"), returns [].
os.insert(4, "ddddd"); // Inserts (4, "ddddd"), returns ["ddddd", "eeeee"].
// Concatentating all the chunks returned:
// [] + ["aaaaa"] + ["bbbbb", "ccccc"] + [] + ["ddddd", "eeeee"] = ["aaaaa", "bbbbb", "ccccc", "ddddd", "eeeee"]
// The resulting order is the same as the order above.

 

Constraints:

• 1 <= n <= 1000
• 1 <= id <= n
• value.length == 5
• value consists only of lowercase letters.
• Each call to insert will have a unique id.
• Exactly n calls will be made to insert.

中文题目

有 n 个 (id, value) 对，其中 id 是 1 到 n 之间的一个整数，value 是一个字符串。不存在 id 相同的两个 (id, value) 对。

设计一个流，以 任意 顺序获取 n 个 (id, value) 对，并在多次调用时 按 id 递增的顺序 返回一些值。

实现 OrderedStream 类：

• OrderedStream(int n) 构造一个能接收 n 个值的流，并将当前指针 ptr 设为 1 。
• String[] insert(int id, String value) 向流中存储新的 (id, value) 对。存储后：
  • 如果流存储有 id = ptr 的 (id, value) 对，则找出从 id = ptr 开始的 最长 id 连续递增序列 ，并 按顺序 返回与这些 id 关联的值的列表。然后，将 ptr 更新为最后那个  id + 1 。

  • 否则，返回一个空列表。

 

示例：

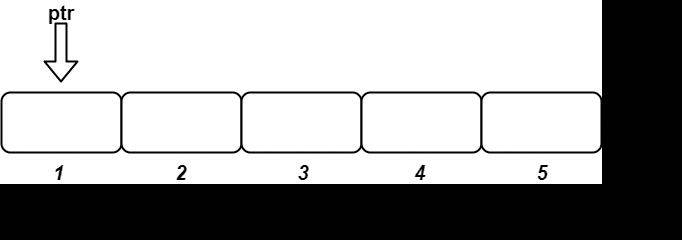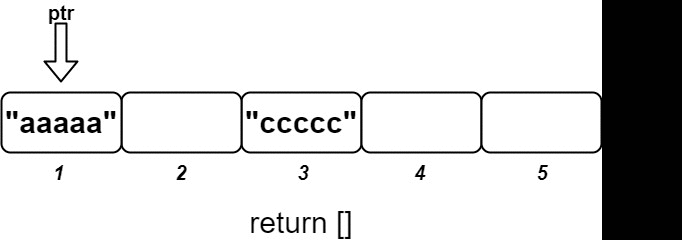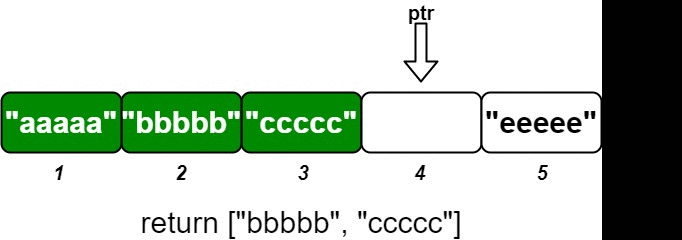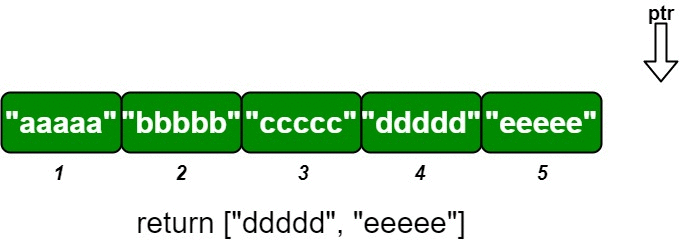
输入
["OrderedStream", "insert", "insert", "insert", "insert", "insert"]
[[5], [3, "ccccc"], [1, "aaaaa"], [2, "bbbbb"], [5, "eeeee"], [4, "ddddd"]]
输出
[null, [], ["aaaaa"], ["bbbbb", "ccccc"], [], ["ddddd", "eeeee"]]

解释
OrderedStream os= new OrderedStream(5);
os.insert(3, "ccccc"); // 插入 (3, "ccccc")，返回 []
os.insert(1, "aaaaa"); // 插入 (1, "aaaaa")，返回 ["aaaaa"]
os.insert(2, "bbbbb"); // 插入 (2, "bbbbb")，返回 ["bbbbb", "ccccc"]
os.insert(5, "eeeee"); // 插入 (5, "eeeee")，返回 []
os.insert(4, "ddddd"); // 插入 (4, "ddddd")，返回 ["ddddd", "eeeee"]

 

提示：

• 1 <= n <= 1000
• 1 <= id <= n
• value.length == 5
• value 仅由小写字母组成
• 每次调用 insert 都会使用一个唯一的 id
• 恰好调用 n 次 insert

通过代码

高赞题解

解题思路

此处撰写解题思路

代码

class OrderedStream {
    String[] a;
    int i=0;

    public OrderedStream(int n) {
        a=new String[n];
        for(int i=0;i<n;i++){
            a[i] = "i";
        }
    }

    public List<String> insert(int idKey, String value) {
        List<String> list = new ArrayList<>();
        if(i != idKey-1){
            a[idKey-1] = value;
            return new ArrayList<String>();
        }else{
            a[idKey-1]=value;
            for(int j=idKey-1;j<a.length;j++){
                if(a[j].equals("i")){
                    i=j;
                    break;
                }
                list.add(a[j]);
            }
            return list;
        }

    }
}
/**
 * Your OrderedStream object will be instantiated and called as such:
 * OrderedStream obj = new OrderedStream(n);
 * List<String> param_1 = obj.insert(idKey,value);
 */

统计信息

通过次数	提交次数	AC比率
8219	10511	78.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言