1971-寻找图中是否存在路径(Find if Path Exists in Graph)

原文链接: https://leetcode-cn.com/problems/find-if-path-exists-in-graph

英文原文

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [u_i, v_i] denotes a bi-directional edge between vertex u_i and vertex v_i. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex start to vertex end.

Given edges and the integers n, start, and end, return true if there is a valid path from start to end, or false otherwise.

Example 1:

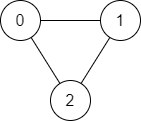
Input: n = 3, edges = [[0,1],[1,2],[2,0]], start = 0, end = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

Example 2:

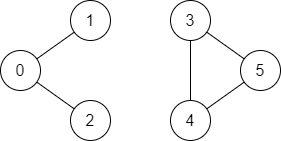
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], start = 0, end = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

Constraints:

1 <= n <= 2 * 10⁵
0 <= edges.length <= 2 * 10⁵
edges[i].length == 2
0 <= u_i, v_i <= n - 1
u_i != v_i
0 <= start, end <= n - 1
There are no duplicate edges.
There are no self edges.

中文题目

有一个具有 n个顶点的双向图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [u_i, v_i] 表示顶点 ui 和顶点 vi 之间的双向边。每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 start 开始，到顶点 end 结束的 有效路径 。

给你数组 edges 和整数 n、start和end，如果从 start 到 end 存在 有效路径 ，则返回 true，否则返回 false 。

示例 1：

输入：n = 3, edges = [[0,1],[1,2],[2,0]], start = 0, end = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2 
- 0 → 2

示例 2：

输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], start = 0, end = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

提示:

1 <= n <= 2 * 10⁵
0 <= edges.length <= 2 * 10⁵
edges[i].length == 2
0 <= u_i, v_i <= n - 1
u_i != v_i
0 <= start, end <= n - 1
不存在双向边
不存在指向顶点自身的边

通过代码

高赞题解

解题思路

没有思路，直接上。

朴素的深度优先

朴素地记录点到点的对应关系，然后使用 dfs 遍历，记住访问过的点防止死循环，毫无疑问超时了；

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int start, int end) {
        vector<vector<int>> graph(n, vector<int>());
        for(vector<int> edge : edges){
            graph[edge[0]].emplace_back(edge[1]);
            graph[edge[1]].emplace_back(edge[0]);
        }

        function<bool(int, vector<bool>)> getRes= [&](int index, vector<bool> isVisited){
            for(int vertex : graph[index]){
                if(!isVisited[vertex]){
                    if(vertex == end)   return true;
                    isVisited[vertex] = true;
                    bool res = getRes(vertex, isVisited);
                    if(res == true) return true;
                    isVisited[vertex] = false;
                }
            }
            return false;
        };
        return getRes(start, vector<bool>(n, false));
    }
};

优化的深度优先

我以为超时的原因是数据量太大数组插入元素耗时太多，所以使用二维矩阵记录图的路径，对图进行深度优先遍历，果然坚持了比前一个多的测试用例，但还是超时了。

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int start, int end) {
        if(start == end)    return true;
        vector<vector<bool>> graph(n, vector<bool>(n, false));
        for(vector<int> edge : edges){
            graph[edge[0]][edge[1]] = graph[edge[1]][edge[0]] = true;
        }
        
        function<bool(int, vector<bool>)> getRes= [&](int index, vector<bool> isVisited){
            for(int vertex = 0; vertex < n; vertex++){
                if(!isVisited[vertex] && graph[index][vertex] == true){
                    if(end == vertex) return true;
                    isVisited[vertex] = true;
                    bool res = getRes(vertex, isVisited);
                    if(res == true) return true;
                    isVisited[vertex] = false; 
                }
            }
            return false;
        };
        return getRes(start, vector<bool>(n, false));
    }
};

寻找连通分支的点集

我太菜了，忘记图怎么找到连通分支了，所以就很常规地寻找每个点能到达的点的集合，加入一个新顶点时，要把集合中所有点和这个顶点相连，最后判断起始点和终止点是否在一个可到达的点集中；

还是那个问题，超时了，循环太多，最坏的情况是每个点都连通，每次都要循环遍历点集。

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int start, int end) {
        if(start == end)    return true;
        vector<set<int>> graph(n, set<int>());
        for(vector<int> edge : edges){
            for(int vertex : graph[edge[0]]){
                graph[vertex].insert(edge[1]);
                graph[edge[1]].insert(vertex);
            }

            for(int vertex : graph[edge[1]]){
                graph[vertex].insert(edge[0]);
                graph[edge[0]].insert(vertex);
            }

            graph[edge[0]].insert(edge[1]);
            graph[edge[1]].insert(edge[0]);
        }

        for(int vertex : graph[start]){
            if(vertex == end)   return true;
        }

        return false;
    }
};

优化找点集

为了避免每次都要遍历点集，我把每个连通分支标号，每个连通分支的顶点映射到各自连通分支的标号；

有点 Dijkstra 那味道，遍历到每条边时，分为三种情况：

1、两个端点都没有归并到一个连通分支中，将两个顶点归并到同一个连通分支，标号记为 sign，然后标记加1，用于下一个新连通分支的标记

2、有一个端点被记录过，另一各端点没有，则将未记录过的端点合并到已记录过端点的连通分支中，即为其赋值为连通分支标号

3、两个端点都被记录过，如果记录的值是同一个连通分支，则跳过；否则，总是以标号较大的那个连通分支作为合并后的连通分支标号（边是随机的，用哪个都行）

使用两个映射结构，vts表示每个顶点映射到的连通分支号，stv表示该连通分支内所有的顶点，每次在需要时更新这两个数据结构；最后，比较起始点和终止点是否在同一个连通分支内即可；可能交的人比较少，达到了双百。

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int start, int end) {
        unordered_map<int, int> vts;    //每个顶点映射到的连通分支号
        unordered_map<int, vector<int>> stv;    //该连通分支内所有的顶点
        int sign = 1;   //连通分支号
        for(vector<int> edge : edges){
            if(vts[edge[0]] > 0 && vts[edge[1]] > 0){   //两个端点都被记录过
                if(vts[edge[0]] == vts[edge[1]])    continue;   //在同一个连通分支
                if(vts[edge[0]] > vts[edge[1]]){   
                    for(int vertex : stv[vts[edge[1]]]){
                        stv[vts[edge[0]]].emplace_back(vertex);
                        vts[vertex] = vts[edge[0]];
                    }
                }
                else{ 
                    for(int vertex : stv[vts[edge[0]]]){
                        stv[vts[edge[1]]].emplace_back(vertex);
                        vts[vertex] = vts[edge[1]];
                    }
                }
            }
            else if(vts[edge[0]] > 0){  //有一个端点被记录过，另一各端点没有
                vts[edge[1]] = vts[edge[0]];
                stv[vts[edge[0]]].emplace_back(edge[1]); 
            }
            else if(vts[edge[1]] > 0){  //有一个端点被记录过，另一各端点没有
                vts[edge[0]] = vts[edge[1]];
                stv[vts[edge[1]]].emplace_back(edge[0]); 
            }
            else{   //两个端点都没有归并到一个连通分支中
                vts[edge[0]] = vts[edge[1]] = sign;
                stv[sign].emplace_back(edge[0]);
                stv[sign].emplace_back(edge[1]);
                sign += 1;
            }
        }
        // for(int i = 0; i < n; i++){
        //     cout<<vts[i]<<" ";
        // }
        return vts[start] == vts[end];
    }
};

(:该去学习大佬们的算法了

统计信息

通过次数	提交次数	AC比率
908	1677	54.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途