英文原文
Given the root of a binary tree, return the sum of every tree node's tilt.
The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if there the node does not have a right child.
Example 1:
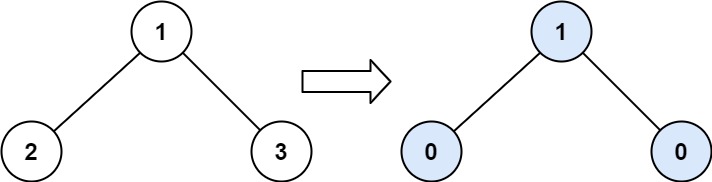
Input: root = [1,2,3] Output: 1 Explanation: Tilt of node 2 : |0-0| = 0 (no children) Tilt of node 3 : |0-0| = 0 (no children) Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3) Sum of every tilt : 0 + 0 + 1 = 1
Example 2:
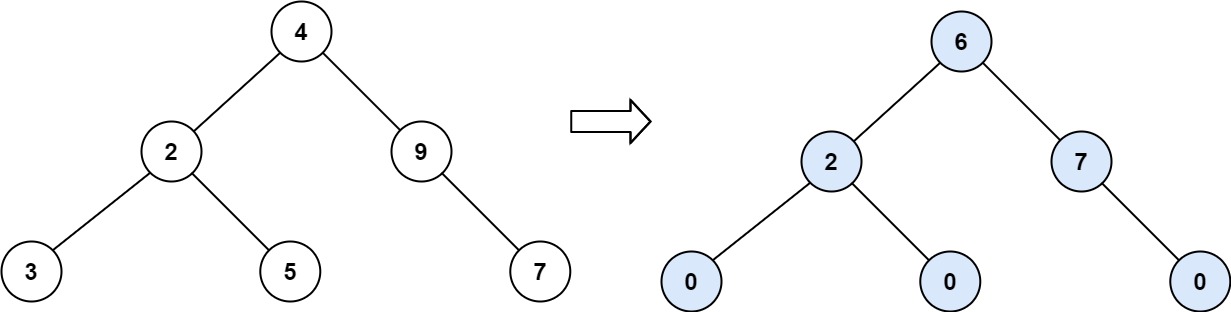
Input: root = [4,2,9,3,5,null,7] Output: 15 Explanation: Tilt of node 3 : |0-0| = 0 (no children) Tilt of node 5 : |0-0| = 0 (no children) Tilt of node 7 : |0-0| = 0 (no children) Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5) Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7) Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16) Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15
Example 3:
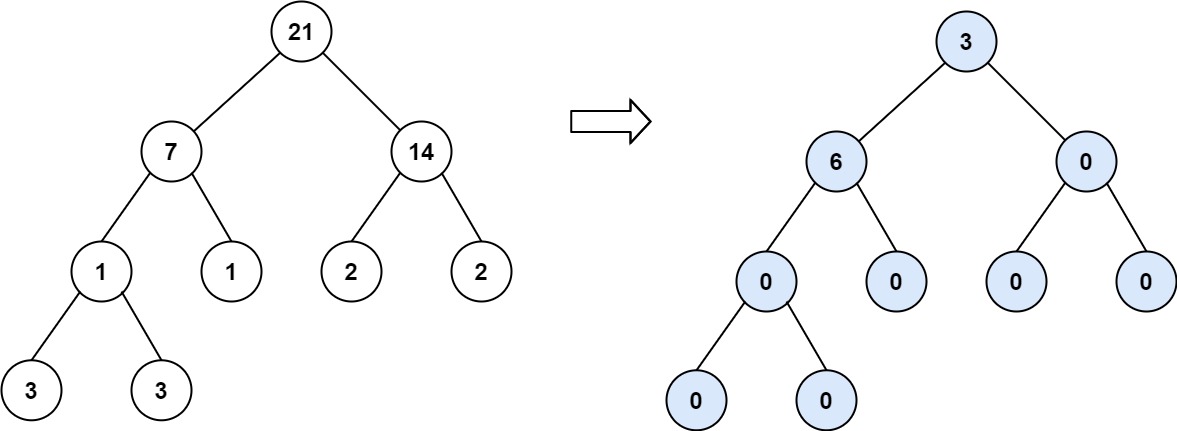
Input: root = [21,7,14,1,1,2,2,3,3] Output: 9
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -1000 <= Node.val <= 1000
中文题目
给定一个二叉树,计算 整个树 的坡度 。
一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为 0 ;没有右子树的话也是一样。空结点的坡度是 0 。
整个树 的坡度就是其所有节点的坡度之和。
示例 1:

输入:root = [1,2,3] 输出:1 解释: 节点 2 的坡度:|0-0| = 0(没有子节点) 节点 3 的坡度:|0-0| = 0(没有子节点) 节点 1 的坡度:|2-3| = 1(左子树就是左子节点,所以和是 2 ;右子树就是右子节点,所以和是 3 ) 坡度总和:0 + 0 + 1 = 1
示例 2:

输入:root = [4,2,9,3,5,null,7] 输出:15 解释: 节点 3 的坡度:|0-0| = 0(没有子节点) 节点 5 的坡度:|0-0| = 0(没有子节点) 节点 7 的坡度:|0-0| = 0(没有子节点) 节点 2 的坡度:|3-5| = 2(左子树就是左子节点,所以和是 3 ;右子树就是右子节点,所以和是 5 ) 节点 9 的坡度:|0-7| = 7(没有左子树,所以和是 0 ;右子树正好是右子节点,所以和是 7 ) 节点 4 的坡度:|(3+5+2)-(9+7)| = |10-16| = 6(左子树值为 3、5 和 2 ,和是 10 ;右子树值为 9 和 7 ,和是 16 ) 坡度总和:0 + 0 + 0 + 2 + 7 + 6 = 15
示例 3:

输入:root = [21,7,14,1,1,2,2,3,3] 输出:9
提示:
- 树中节点数目的范围在
[0, 104]内 -1000 <= Node.val <= 1000
通过代码
高赞题解
递归
根据题目对「坡度」的定义,我们可以直接写出对应的递归实现。
代码:
[]class Solution { public int findTilt(TreeNode root) { if (root == null) return 0; return findTilt(root.left) + findTilt(root.right) + Math.abs(getSum(root.left) - getSum(root.right)); } int getSum(TreeNode root) { if (root == null) return 0; return getSum(root.left) + getSum(root.right) + root.val; } }
- 时间复杂度:每个节点被访问的次数与其所在深度有关。复杂度为 $O(n^2)$
- 空间复杂度:忽略递归来带的额外空间消耗。复杂度为 $O(1)$
递归
上述解法之所以为 $O(n^2)$ 的时间复杂度,是因为我们将「计算子树坡度」和「计算子树权值和」两个操作分开进行。
事实上,我们可以在计算子树权值和的时候将坡度进行累加,从而将复杂度降为 $O(n)$。
代码:
[]class Solution { int ans; public int findTilt(TreeNode root) { dfs(root); return ans; } int dfs(TreeNode root) { if (root == null) return 0; int l = dfs(root.left), r = dfs(root.right); ans += Math.abs(l - r); return l + r + root.val; } }
- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
其他与「二叉树」相关内容
考虑加练如下「二叉树」题目 🍭🍭
| 题目 | 题解 | 难度 | 推荐指数 |
|---|---|---|---|
| 230. 二叉搜索树中第K小的元素 | LeetCode 题解链接 | 中等 | 🤩🤩🤩🤩 |
| 240. 搜索二维矩阵 II | LeetCode 题解链接 | 中等 | 🤩🤩🤩🤩 |
| 297. 二叉树的序列化与反序列化 | LeetCode 题解链接 | 困难 | 🤩🤩🤩🤩🤩 |
| 437. 路径总和 III | LeetCode 题解链接 | 中等 | 🤩🤩🤩🤩 |
| 783. 二叉搜索树节点最小距离 | LeetCode 题解链接 | 简单 | 🤩🤩🤩 |
| 863. 二叉树中所有距离为 K 的结点 | LeetCode 题解链接 | 中等 | 🤩🤩🤩🤩 |
| 938. 二叉搜索树的范围和 | LeetCode 题解链接 | 简单 | 🤩🤩🤩 |
| 987. 二叉树的垂序遍历 | LeetCode 题解链接 | 困难 | 🤩🤩🤩🤩🤩 |
| 993. 二叉树的堂兄弟节点 | LeetCode 题解链接 | 简单 | 🤩🤩 |
| 1104. 二叉树寻路 | LeetCode 题解链接 | 中等 | 🤩🤩🤩 |
| 剑指 Offer 37. 序列化二叉树 | LeetCode 题解链接 | 困难 | 🤩🤩🤩🤩🤩 |
注:以上目录整理来自 wiki,任何形式的转载引用请保留出处。
最后
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ (“▔□▔)/
也欢迎你 关注我(公主号后台回复「送书」即可参与长期看题解学算法送实体书活动)或 加入「组队打卡」小群 ,提供写「证明」&「思路」的高质量题解。
所有题解已经加入 刷题指南,欢迎 star 哦 ~
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 59511 | 90922 | 65.5% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




