原文链接: https://leetcode-cn.com/problems/reshape-the-matrix

英文原文

In MATLAB, there is a handy function called reshape which can reshape an m x n matrix into a new one with a different size r x c keeping its original data.

You are given an m x n matrix mat and two integers r and c representing the number of rows and the number of columns of the wanted reshaped matrix.

The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.

If the reshape operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.

 

Example 1:

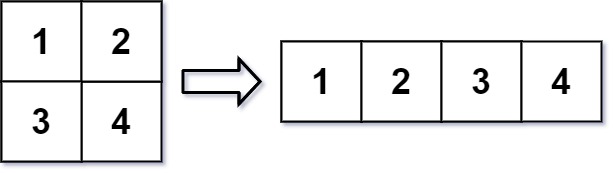
Input: mat = [[1,2],[3,4]], r = 1, c = 4
Output: [[1,2,3,4]]

Example 2:

Input: mat = [[1,2],[3,4]], r = 2, c = 4
Output: [[1,2],[3,4]]

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• -1000 <= mat[i][j] <= 1000
• 1 <= r, c <= 300

中文题目

在 MATLAB 中，有一个非常有用的函数 reshape ，它可以将一个 m x n 矩阵重塑为另一个大小不同（r x c）的新矩阵，但保留其原始数据。

给你一个由二维数组 mat 表示的 m x n 矩阵，以及两个正整数 r 和 c ，分别表示想要的重构的矩阵的行数和列数。

重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。

如果具有给定参数的 reshape 操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

 

示例 1：

输入：mat = [[1,2],[3,4]], r = 1, c = 4
输出：[[1,2,3,4]]

示例 2：

输入：mat = [[1,2],[3,4]], r = 2, c = 4
输出：[[1,2],[3,4]]

 

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• -1000 <= mat[i][j] <= 1000
• 1 <= r, c <= 300

通过代码

高赞题解

方法一：二维数组的一维表示

思路与算法

对于一个行数为 $m$，列数为 $n$，行列下标都从 $0$ 开始编号的二维数组，我们可以通过下面的方式，将其中的每个元素 $(i, j)$ 映射到整数域内，并且它们按照行优先的顺序一一对应着 $[0, mn)$ 中的每一个整数。形象化地来说，我们把这个二维数组「排扁」成了一个一维数组。如果读者对机器学习有一定了解，可以知道这就是 $\texttt{flatten}$ 操作。

这样的映射即为：

$$
(i, j) \to i \times n+j
$$

同样地，我们可以将整数 $x$ 映射回其在矩阵中的下标，即

$$
\begin{cases}
i = x / n \
j = x % n
\end{cases}
$$

其中 $/$ 表示整数除法，$%$ 表示取模运算。

那么题目需要我们做的事情相当于：

• 将二维数组 $\textit{nums}$ 映射成一个一维数组；

• 将这个一维数组映射回 $r$ 行 $c$ 列的二维数组。

我们当然可以直接使用一个一维数组进行过渡，但我们也可以直接从二维数组 $\textit{nums}$ 得到 $r$ 行 $c$ 列的重塑矩阵：

• 设 $\textit{nums}$ 本身为 $m$ 行 $n$ 列，如果 $mn \neq rc$，那么二者包含的元素个数不相同，因此无法进行重塑；

• 否则，对于 $x \in [0, mn)$，第 $x$ 个元素在 $\textit{nums}$ 中对应的下标为 $(x / n, x% n)$，而在新的重塑矩阵中对应的下标为 $(x / c, x% c)$。我们直接进行赋值即可。

代码

[sol1-C++]
class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& nums, int r, int c) {
        int m = nums.size();
        int n = nums[0].size();
        if (m * n != r * c) {
            return nums;
        }

        vector<vector<int>> ans(r, vector<int>(c));
        for (int x = 0; x < m * n; ++x) {
            ans[x / c][x % c] = nums[x / n][x % n];
        }
        return ans;
    }
};

[sol1-Java]
class Solution {
    public int[][] matrixReshape(int[][] nums, int r, int c) {
        int m = nums.length;
        int n = nums[0].length;
        if (m * n != r * c) {
            return nums;
        }

        int[][] ans = new int[r][c];
        for (int x = 0; x < m * n; ++x) {
            ans[x / c][x % c] = nums[x / n][x % n];
        }
        return ans;
    }
}

[sol1-Python3]
class Solution:
    def matrixReshape(self, nums: List[List[int]], r: int, c: int) -> List[List[int]]:
        m, n = len(nums), len(nums[0])
        if m * n != r * c:
            return nums
        
        ans = [[0] * c for _ in range(r)]
        for x in range(m * n):
            ans[x // c][x % c] = nums[x // n][x % n]
        
        return ans

[sol1-JavaScript]
var matrixReshape = function(nums, r, c) {
    const m = nums.length;
    const n = nums[0].length;
    if (m * n != r * c) {
        return nums;
    }

    const ans = new Array(r).fill(0).map(() => new Array(c).fill(0));
    for (let x = 0; x < m * n; ++x) {
        ans[Math.floor(x / c)][x % c] = nums[Math.floor(x / n)][x % n];
    }
    return ans;
};

[sol1-Golang]
func matrixReshape(nums [][]int, r int, c int) [][]int {
    n, m := len(nums), len(nums[0])
    if n*m != r*c {
        return nums
    }
    ans := make([][]int, r)
    for i := range ans {
        ans[i] = make([]int, c)
    }
    for i := 0; i < n*m; i++ {
        ans[i/c][i%c] = nums[i/m][i%m]
    }
    return ans
}

[sol1-C]
int** matrixReshape(int** nums, int numsSize, int* numsColSize, int r, int c, int* returnSize, int** returnColumnSizes) {
    int m = numsSize;
    int n = numsColSize[0];
    if (m * n != r * c) {
        *returnSize = numsSize;
        *returnColumnSizes = numsColSize;
        return nums;
    }
    *returnSize = r;
    *returnColumnSizes = malloc(sizeof(int) * r);
    int** ans = malloc(sizeof(int*) * r);

    for (int i = 0; i < r; i++) {
        (*returnColumnSizes)[i] = c;
        ans[i] = malloc(sizeof(int) * c);
    }
    for (int x = 0; x < m * n; ++x) {
        ans[x / c][x % c] = nums[x / n][x % n];
    }
    return ans;
}

复杂度分析

• 时间复杂度：$O(rc)$。这里的时间复杂度是在重塑矩阵成功的前提下的时间复杂度，否则当 $mn \neq rc$ 时，$\texttt{C++}$ 语言中返回的是原数组的一份拷贝，本质上需要的时间复杂度为 $O(mn)$，而其余语言可以直接返回原数组的对象，需要的时间复杂度仅为 $O(1)$。

• 空间复杂度：$O(1)$。这里的空间复杂度不包含返回的重塑矩阵需要的空间。

统计信息

通过次数	提交次数	AC比率
77468	113768	68.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言