原文链接: https://leetcode-cn.com/problems/toeplitz-matrix

英文原文

Given an m x n matrix, return true if the matrix is Toeplitz. Otherwise, return false.

A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same elements.

 

Example 1:

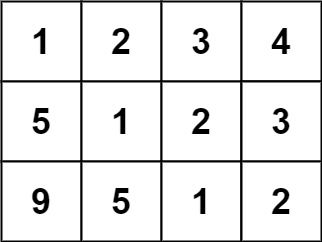
Input: matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
Output: true
Explanation:
In the above grid, the diagonals are:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]".
In each diagonal all elements are the same, so the answer is True.

Example 2:

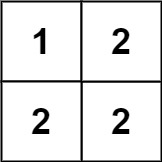
Input: matrix = [[1,2],[2,2]]
Output: false
Explanation:
The diagonal "[1, 2]" has different elements.

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 20
• 0 <= matrix[i][j] <= 99

 

Follow up:

• What if the matrix is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
• What if the matrix is so large that you can only load up a partial row into the memory at once?

中文题目

给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵，返回 true ；否则，返回 false 。

如果矩阵上每一条由左上到右下的对角线上的元素都相同，那么这个矩阵是 托普利茨矩阵 。

 

示例 1：

输入：matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
输出：true
解释：
在上述矩阵中, 其对角线为: 
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]"。 
各条对角线上的所有元素均相同, 因此答案是 True 。

示例 2：

输入：matrix = [[1,2],[2,2]]
输出：false
解释：
对角线 "[1, 2]" 上的元素不同。

 

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 20
• 0 <= matrix[i][j] <= 99

 

进阶：

• 如果矩阵存储在磁盘上，并且内存有限，以至于一次最多只能将矩阵的一行加载到内存中，该怎么办？
• 如果矩阵太大，以至于一次只能将不完整的一行加载到内存中，该怎么办？

通过代码

高赞题解

各位题友大家好！ 今天是 @负雪明烛 坚持日更的第 29 天。今天力扣上的每日一题是「766. 托普利茨矩阵」。

解题思路

• 解题思路：每一个位置都要跟其右下角的元素相等。

我以前做这个题的时候选择了一个笨方法：遍历每条对角线，判断每条对角线上元素是否都相等。很显然，这个做法是直接按照托普利茨矩阵定义写的，但是由于对角线比较多，导致代码比较复杂。

现在，我是这么做的：只要每个元素都跟其右下角元素相等就行了。只要这样遍历结束之后，就能保证所有对角线上的元素就都是相等的。

以题目示例一为例的动图如下：

代码

在 Python 代码中我用了切片操作，第 $i$ 行的 $[0, N - 2]$的切片等于第 $i + 1$ 行的 $[1, N - 1]$，这样能节省代码长度。

Python, C++, Java 代码如下：

[]
class Solution:
    def isToeplitzMatrix(self, matrix: List[List[int]]) -> bool:
        for i in range(len(matrix) - 1):
            if matrix[i][:-1] != matrix[i + 1][1:]:
                return False
        return True

[]
class Solution {
public:
    bool isToeplitzMatrix(vector<vector<int>>& matrix) {
        for (int i = 0; i < matrix.size() - 1; ++i) {
            for (int j = 0; j < matrix[0].size() - 1; ++j) {
                if (matrix[i][j] != matrix[i + 1][j + 1])
                    return false;
            }
        }
        return true;
    }
};

[]
class Solution {
    public boolean isToeplitzMatrix(int[][] matrix) {
        for (int i = 0; i < matrix.length - 1; ++i) {
            for (int j = 0; j < matrix[0].length - 1; ++j) {
                if (matrix[i][j] != matrix[i + 1][j + 1])
                    return false;
            }
        }
        return true;
    }
}

刷题心得

• 每次做题都会有新体会，坚持刷题，就一定会有收获。
• 多看看别人的优秀题解，能学到很多东西。

---

OK，以上就是 @负雪明烛 写的今天题解的全部内容了，如果你觉得有帮助的话，求赞、求关注、求收藏。如果有疑问的话，请在下面评论，我会及时解答。

关注我，你将不会错过我的精彩动画题解、面试题分享、组队刷题活动，进入主页 @负雪明烛 右侧有刷题组织，从此刷题不再孤单。

祝大家牛年大吉！AC 多多，Offer 多多！我们明天再见！

统计信息

通过次数	提交次数	AC比率
56266	79492	70.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
有效的单词方块	简单