原文链接: https://leetcode-cn.com/problems/projection-area-of-3d-shapes

英文原文

You are given an n x n grid where we place some 1 x 1 x 1 cubes that are axis-aligned with the x, y, and z axes.

Each value v = grid[i][j] represents a tower of v cubes placed on top of the cell (i, j).

We view the projection of these cubes onto the xy, yz, and zx planes.

A projection is like a shadow, that maps our 3-dimensional figure to a 2-dimensional plane. We are viewing the "shadow" when looking at the cubes from the top, the front, and the side.

Return the total area of all three projections.

 

Example 1:

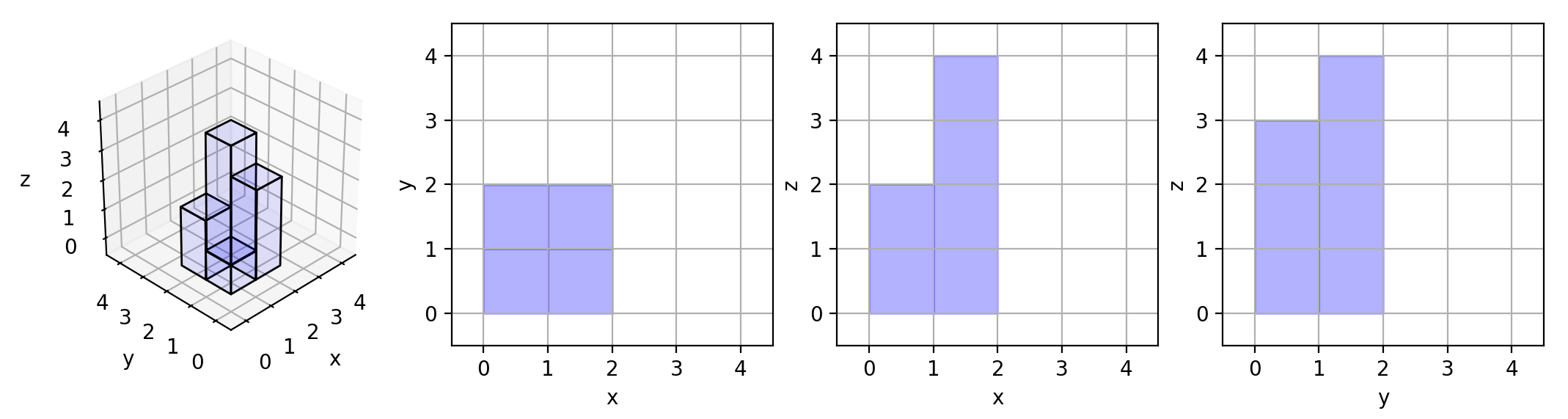
Input: grid = [[1,2],[3,4]]
Output: 17
Explanation: Here are the three projections ("shadows") of the shape made with each axis-aligned plane.

Example 2:

Input: grid = [[2]]
Output: 5

Example 3:

Input: grid = [[1,0],[0,2]]
Output: 8

Example 4:

Input: grid = [[1,1,1],[1,0,1],[1,1,1]]
Output: 14

Example 5:

Input: grid = [[2,2,2],[2,1,2],[2,2,2]]
Output: 21

 

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

中文题目

在 N * N 的网格中，我们放置了一些与 x，y，z 三轴对齐的 1 * 1 * 1 立方体。

每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。

现在，我们查看这些立方体在 xy、yz 和 zx 平面上的投影。

投影就像影子，将三维形体映射到一个二维平面上。

在这里，从顶部、前面和侧面看立方体时，我们会看到“影子”。

返回所有三个投影的总面积。

 

示例 1：

输入：[[2]]
输出：5

示例 2：

输入：[[1,2],[3,4]]
输出：17
解释：
这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

示例 3：

输入：[[1,0],[0,2]]
输出：8

示例 4：

输入：[[1,1,1],[1,0,1],[1,1,1]]
输出：14

示例 5：

输入：[[2,2,2],[2,1,2],[2,2,2]]
输出：21

 

提示：

• 1 <= grid.length = grid[0].length <= 50
• 0 <= grid[i][j] <= 50

通过代码

官方题解

方法：数学

思路和算法

从顶部看，由该形状生成的阴影将是网格中非零值的数目。

从侧面看，由该形状生成的阴影将是网格中每一行的最大值。

从前面看，由该形状生成的阴影将是网格中每一列的最大值。

示例

例如 [[1,2],[3,4]]：

• 顶部的阴影将为 4，因为网格中有四个非零值;

• 侧面的阴影为 2 + 4，因为第一行的最大值为 2，第二行的最大值为 4;

• 前面的阴影是 3 + 4，因为第一列的最大值是 3，第二列的最大值是 4。

[DoBY8EpQ-C++]
class Solution {
public:
    int projectionArea(vector<vector<int>>& grid) {
        int N = grid.size();
        int ans = 0;

        for (int i = 0; i < N;  ++i) {
            int bestRow = 0;  // largest of grid[i][j]
            int bestCol = 0;  // largest of grid[j][i]
            for (int j = 0; j < N; ++j) {
                if (grid[i][j] > 0) ans++;  // top shadow
                bestRow = max(bestRow, grid[i][j]);
                bestCol = max(bestCol, grid[j][i]);
            }
            ans += bestRow + bestCol;
        }

        return ans;
    }
};

[DoBY8EpQ-Java]
class Solution {
    public int projectionArea(int[][] grid) {
        int N = grid.length;
        int ans = 0;

        for (int i = 0; i < N;  ++i) {
            int bestRow = 0;  // largest of grid[i][j]
            int bestCol = 0;  // largest of grid[j][i]
            for (int j = 0; j < N; ++j) {
                if (grid[i][j] > 0) ans++;  // top shadow
                bestRow = Math.max(bestRow, grid[i][j]);
                bestCol = Math.max(bestCol, grid[j][i]);
            }
            ans += bestRow + bestCol;
        }

        return ans;
    }
}

[DoBY8EpQ-Python]
class Solution:
    def projectionArea(self, grid):
        N = len(grid)
        ans = 0

        for i in xrange(N):
            best_row = 0  # max of grid[i][j]
            best_col = 0  # max of grid[j][i]
            for j in xrange(N):
                if grid[i][j]: ans += 1  # top shadow
                best_row = max(best_row, grid[i][j])
                best_col = max(best_col, grid[j][i])

            ans += best_row + best_col

        return ans

        """ Alternative solution:
        ans = sum(map(max, grid))
        ans += sum(map(max, zip(*grid)))
        ans += sum(v > 0 for row in grid for v in row)
        """

复杂度分析

• 时间复杂度：$O(N^2)$，其中 $N$ 是 grid 的长度。

• 空间复杂度：$O(1)$.

统计信息

通过次数	提交次数	AC比率
11285	16316	69.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言