原文链接: https://leetcode-cn.com/problems/increasing-order-search-tree
英文原文
Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
Example 1:
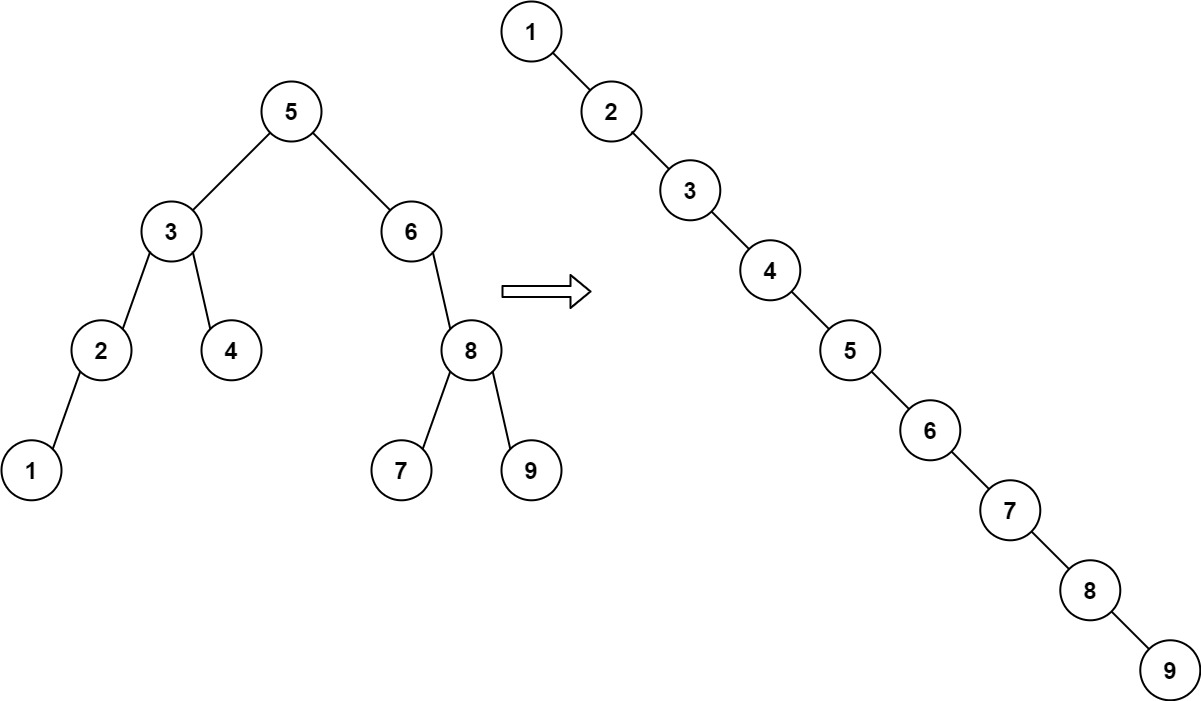
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9] Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
Example 2:
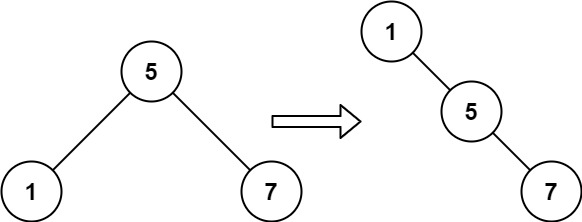
Input: root = [5,1,7] Output: [1,null,5,null,7]
Constraints:
- The number of nodes in the given tree will be in the range
[1, 100]. 0 <= Node.val <= 1000
中文题目
给你一棵二叉搜索树,请你 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
示例 1:

输入:root = [5,3,6,2,4,null,8,1,null,null,null,7,9] 输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
示例 2:

输入:root = [5,1,7] 输出:[1,null,5,null,7]
提示:
- 树中节点数的取值范围是
[1, 100] 0 <= Node.val <= 1000
通过代码
高赞题解
各位题友大家好! 今天是 @负雪明烛 坚持日更的第 86 天。今天力扣上的每日一题是「897. 递增顺序搜索树」。
解题思路
题意:把一棵「二叉搜索树」按照中序遍历构成一棵每个节点都只有右孩子的树。与不久前的每日一题「783. 二叉搜索树节点最小距离」是极其相似的题目。
遇到二叉搜索树,立刻想到这句话:「二叉搜索树(BST)的中序遍历是有序的」。这是解决所有二叉搜索树问题的关键。
本题已经告诉我们使用中序遍历,其实对于二叉搜索树而言,只要让我们得到有序的遍历结果,那么一定要想到中序遍历。
分享二叉树遍历的经验:先序、中序、后序遍历方式的区别在于把「执行操作」放在两个递归函数的位置。伪代码在下面。
- 先序遍历:
[]def dfs(root): if not root: return 执行操作 dfs(root.left) dfs(root.right)
- 中序遍历:
[]def dfs(root): if not root: return dfs(root.left) 执行操作 dfs(root.right)
- 后序遍历:
[]def dfs(root): if not root: return dfs(root.left) dfs(root.right) 执行操作
本题是使用了中序遍历,所以把「执行操作」这一步改成自己想要的代码。用本题作为示例。
于是有了下面两种写法。
方法一:数组保存中序遍历结果
这个方法是最直观的,也不容易出错的。
- 先中序遍历,把结果放在数组中;
- 然后修改数组中每个节点的左右指针:把节点的左指针设置为 null,把节点的右指针设置为数组的下一个节点。
下面的代码中,使用了 dummy (哑节点),它一般在链表题中出现。在链表题目中,我们为了防止链表的头结点发生变化之后,不好维护头结点,我们设置 dummy 从而保证头结点不变。这个题目中设置了 dummy ,从而保证了在新的树中,dummy 是根节点,最终返回的时候,要返回的是 dummy.right。
[]# Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): def increasingBST(self, root): self.res = [] self.inOrder(root) if not self.res: return dummy = TreeNode(-1) cur = dummy for node in self.res: node.left = node.right = None cur.right = node cur = cur.right return dummy.right def inOrder(self, root): if not root: return self.inOrder(root.left) self.res.append(root) self.inOrder(root.right)
- 时间复杂度:$O(N)$,因为每个节点只访问了一次;
- 空间复杂度:$O(N)$,因为需要数组保存二叉树的每个节点值。
方法二:只保存上个节点
在方法一中,我们保存了整个中序遍历数组,比较浪费空间。
其实我们只需要知道,在中序遍历的时候的两个被依次访问的节点。注意,这里说的不是 BST 的相邻节点,因为在中序遍历时,在访问根节点前,上一个被访问的节点是其左子树的最右下角的节点。如下图所示,访问 节点4 之前,访问的是节点3。

所以,我们只需要一个变量 prev 保存在中序遍历时,上一次被访问的节点。那么我们每次遍历的时候:
- 把当前节点
root.left设置为null; - 把
prev.right设置为当前遍历的节点root; - 把当前
root设置为prev。
这样的话,就保证了在中序遍历的过程中的访问顺序,形成了一个新的只有右孩子的树。
上图中,在完成中序遍历之后,新的树的结构就是按照图中的红色箭头 1 -①-> 2 -②-> 3 -③-> 4 -④-> 6 。
代码中同样地,我们设置一个 dummy 节点当做新的树的根节点,并把它作为默认的 prev 节点。
代码如下:
[]# Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): def increasingBST(self, root): dummy = TreeNode(-1) self.prev = dummy self.inOrder(root) return dummy.right def inOrder(self, root): if not root: return None self.inOrder(root.left) root.left = None self.prev.right = root self.prev = root self.inOrder(root.right)
- 时间复杂度:$O(N)$,因为每个节点只访问了一次;
- 空间复杂度:$O(N)$,因为递归用了系统栈。
刷题心得
在最近几个月的刷每日一题的过程中,已经发现有多次题目都是高度类似的。掌握一道题,掌握一种方法,然后反复练习,下次再遇到类似的题目,应该就会做了。
参考资料:
897. Increasing Order Search Tree
OK,以上就是 @负雪明烛 写的今天题解的全部内容了,如果你觉得有帮助的话,求赞、求关注、求收藏。如果有疑问的话,请在下面评论,我会及时解答。
关注我,你将不会错过我的精彩动画题解、面试题分享、组队刷题活动,进入主页 @负雪明烛 右侧有刷题组织,从此刷题不再孤单。
祝大家 AC 多多,Offer 多多!我们明天再见!
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 63752 | 85801 | 74.3% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




