原文链接: https://leetcode-cn.com/problems/univalued-binary-tree

英文原文

A binary tree is uni-valued if every node in the tree has the same value.

Given the root of a binary tree, return true if the given tree is uni-valued, or false otherwise.

 

Example 1:

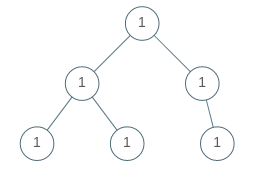
Input: root = [1,1,1,1,1,null,1]
Output: true

Example 2:

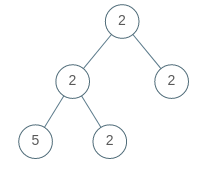
Input: root = [2,2,2,5,2]
Output: false

 

Constraints:

• The number of nodes in the tree is in the range [1, 100].
• 0 <= Node.val < 100

中文题目

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回 true；否则返回 false。

 

示例 1：

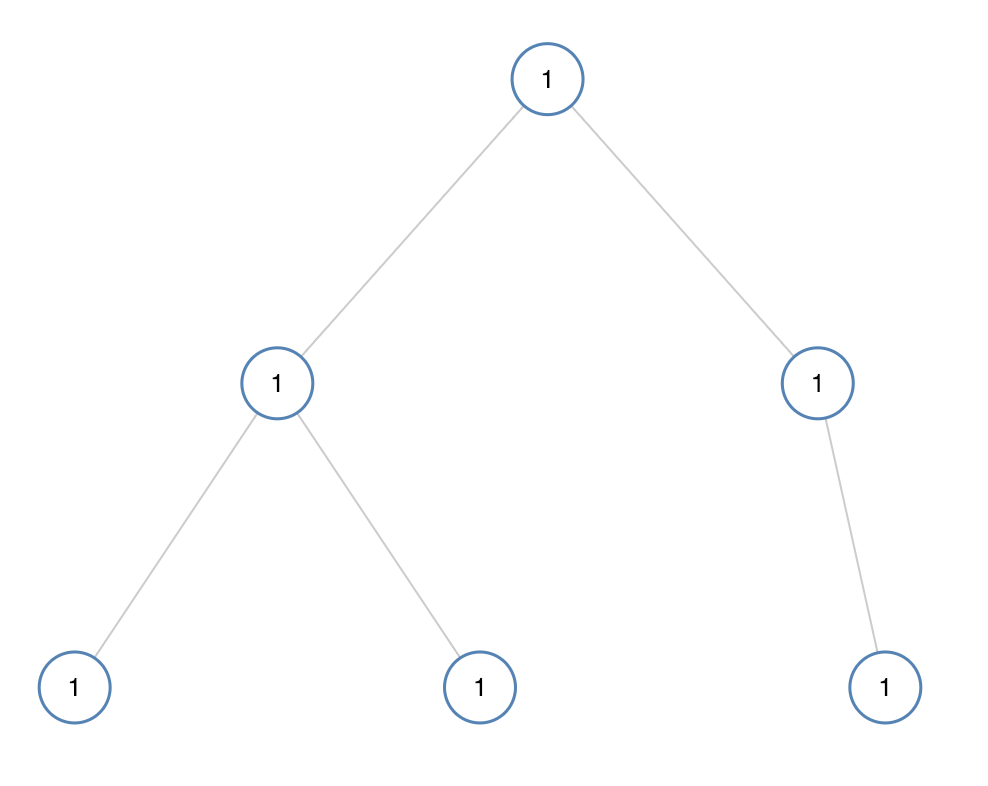
输入：[1,1,1,1,1,null,1]
输出：true

示例 2：

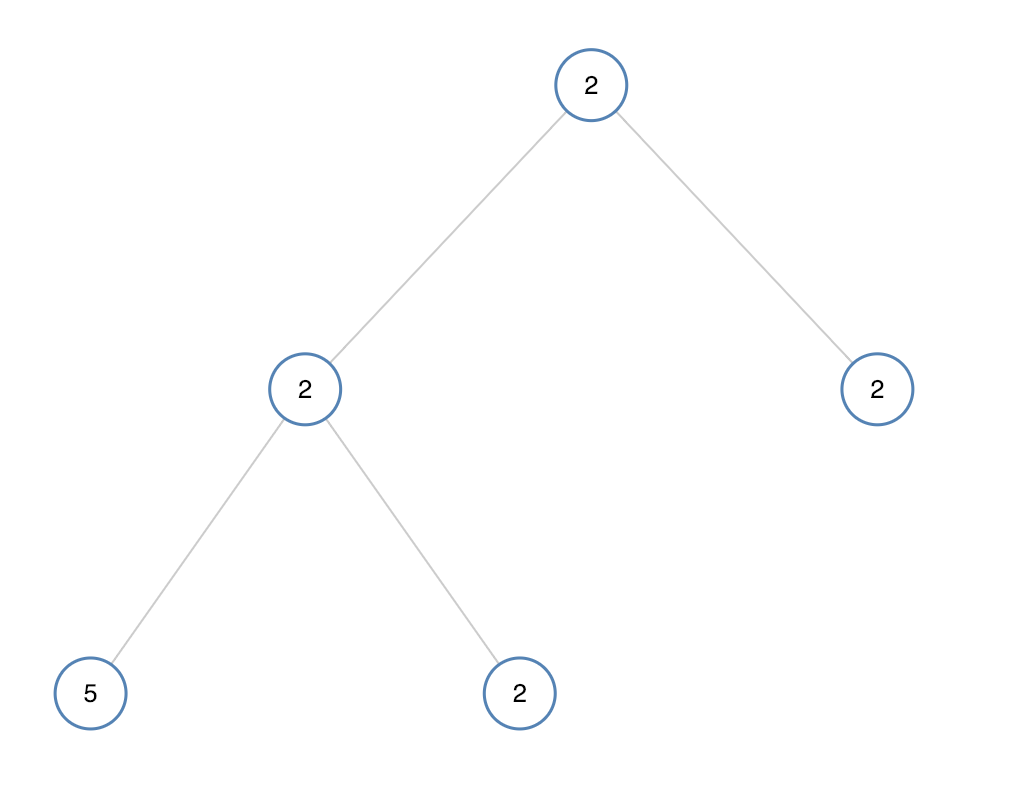
输入：[2,2,2,5,2]
输出：false

 

提示：

1. 给定树的节点数范围是 [1, 100]。
2. 每个节点的值都是整数，范围为 [0, 99] 。

通过代码

官方题解

方法一：深度优先搜索

思路与算法

我们先进行一次深度优先搜索，获取这颗树中的所有节点的值。然后，就可以判断所有节点的值是不是都相等了。

[himT7fHE-Java]
class Solution {
    List<Integer> vals;
    public boolean isUnivalTree(TreeNode root) {
        vals = new ArrayList();
        dfs(root);
        for (int v: vals)
            if (v != vals.get(0))
                return false;
        return true;
    }

    public void dfs(TreeNode node) {
        if (node != null) {
            vals.add(node.val);
            dfs(node.left);
            dfs(node.right);
        }
    }
}

[himT7fHE-Python]
class Solution(object):
    def isUnivalTree(self, root):
        vals = []

        def dfs(node):
            if node:
                vals.append(node.val)
                dfs(node.left)
                dfs(node.right)

        dfs(root)
        return len(set(vals)) == 1

复杂度分析

• 时间复杂度：$O(N)$，其中 $N$ 是给定树中节点的数量。

• 空间复杂度：$O(N)$。

---

方法二：递归

思路与算法

一颗树是单值的，当且仅当根节点的子节点所在的子树也是单值的，同时根节点的值与子节点的值相同。

我们可以使用递归实现这个判断的过程。left_correct 表示当前节点的左孩子是正确的，也就是说：左孩子所在的子树是单值的，并且当前节点的值等于左孩子的值。right_correct 对当前节点的右孩子表示同样的事情。递归处理之后，当根节点的这两种属性都为真的时候，我们就可以判定这颗二叉树是单值的。

[5GyAMr2y-Java]
class Solution {
    public boolean isUnivalTree(TreeNode root) {
        boolean left_correct = (root.left == null ||
                (root.val == root.left.val && isUnivalTree(root.left)));
        boolean right_correct = (root.right == null ||
                (root.val == root.right.val && isUnivalTree(root.right)));
        return left_correct && right_correct;
    }
}

[5GyAMr2y-Python]
class Solution(object):
    def isUnivalTree(self, root):
        left_correct = (not root.left or root.val == root.left.val
                and self.isUnivalTree(root.left))
        right_correct = (not root.right or root.val == root.right.val
                and self.isUnivalTree(root.right))
        return left_correct and right_correct

复杂度分析

• 时间复杂度：$O(N)$，其中 $N$ 是给定树中节点的数量。

• 空间复杂度：$O(H)$，其中 $H$ 是给定树的高度。

统计信息

通过次数	提交次数	AC比率
34915	51015	68.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言