原文链接: https://leetcode-cn.com/problems/cousins-in-binary-tree

英文原文

Given the root of a binary tree with unique values and the values of two different nodes of the tree x and y, return true if the nodes corresponding to the values x and y in the tree are cousins, or false otherwise.

Two nodes of a binary tree are cousins if they have the same depth with different parents.

Note that in a binary tree, the root node is at the depth 0, and children of each depth k node are at the depth k + 1.

 

Example 1:

Input: root = [1,2,3,4], x = 4, y = 3
Output: false

Example 2:

Input: root = [1,2,3,null,4,null,5], x = 5, y = 4
Output: true

Example 3:

Input: root = [1,2,3,null,4], x = 2, y = 3
Output: false

 

Constraints:

• The number of nodes in the tree is in the range [2, 100].
• 1 <= Node.val <= 100
• Each node has a unique value.
• x != y
• x and y are exist in the tree.

中文题目

在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。

如果二叉树的两个节点深度相同，但 父节点不同 ，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root ，以及树中两个不同节点的值 x 和 y 。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true 。否则，返回 false。

 

示例 1：

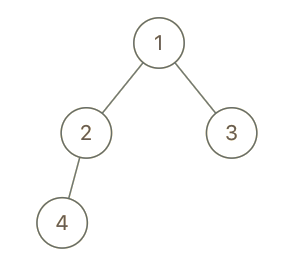
输入：root = [1,2,3,4], x = 4, y = 3
输出：false

示例 2：

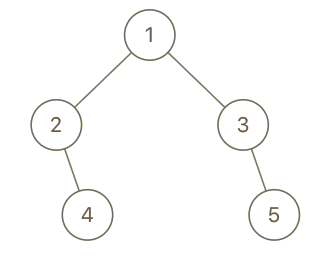
输入：root = [1,2,3,null,4,null,5], x = 5, y = 4
输出：true

示例 3：

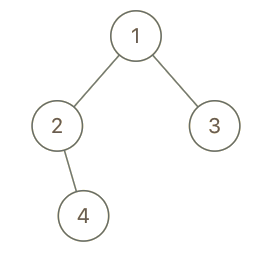
输入：root = [1,2,3,null,4], x = 2, y = 3
输出：false

 

提示：

• 二叉树的节点数介于 2 到 100 之间。
• 每个节点的值都是唯一的、范围为 1 到 100 的整数。

 

通过代码

高赞题解

解题思路

这道题目当然用BFS或者DFS都可以做，但是用DFS是不如BFS优雅的。
细节是魔鬼，本题有两个关键点：

1. 深度相同
2. 父节点不同

在确定深度上面，BFS一直很可以的。
具体思路如下：
因为在BFS中，我们使用的是层序遍历，如果每次遍历一层，那么这一层的元素的深度是相同的。
例子：（第i层深度为i）
{:width=200}
第一层: [1]
第二层：[2,3]
第三层：[4,5,6,7]

因此我们在每一层，看看是否有出现 x 和 y，其中分为以下三种情况：

1. x 和 y 都没出现 → 那只能往下一层继续找了
2. x 和 y 只出现一个 → 两个元素的深度不同，不可能为兄弟，返回false
3. x 和 y 都出现了，好耶，但是还不够好
   • x 和 y 父节点相同 → 不是堂兄弟，是亲兄弟，不行，返回false
   • x 和 y 父节点不同 → 满足题目条件了，好耶，返回true

众所周知，BFS需要用到队列，那么我们应该如何设计队列的数据类型？
在这里，我采用了 pair<TreeNode*, TreeNode*>（其实pair<TreeNode*, int>也可以），其中pair中，第一个元素记录指向当前结点的指针，第二个元素记录指向当前结点的父结点的指针，这样就可以完美应对上面所说的三种情况了。

代码

class Solution {
public:
    using PTT = pair<TreeNode*, TreeNode*>;
    bool isCousins(TreeNode* root, int x, int y) {
        // 使用队列q来进行bfs
        // 其中pair中，p.first 记录当前结点的指针，p.second 记录当前结点的父结点的指针
        queue<PTT> q;
        q.push({root, nullptr});
        while(!q.empty()) {
            int n = q.size();
            vector<TreeNode*> rec_parent;
            for(int i = 0; i < n; i++) {
                auto [cur, parent] = q.front(); q.pop();
                if(cur->val == x || cur->val == y)
                    rec_parent.push_back(parent);
                if(cur->left) q.push({cur->left, cur});
                if(cur->right) q.push({cur->right, cur});
            }
            // `x` 和 `y` 都没出现
            if(rec_parent.size() == 0)
                continue;
            // `x` 和 `y` 只出现一个
            else if(rec_parent.size() == 1)
                return false;
            // `x` 和 `y` 都出现了
            else if(rec_parent.size() == 2)
                // `x` 和 `y` 父节点 相同/不相同 ？
                return rec_parent[0] != rec_parent[1];
        }
        return false;
    }
};

统计信息

通过次数	提交次数	AC比率
52534	94288	55.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
二叉树的层序遍历	中等