原文链接: https://leetcode-cn.com/problems/SNJvJP

英文原文

中文题目

某乐团的演出场地可视作 `num * num` 的二维矩阵 `grid`（左上角坐标为 `[0,0]`)，每个位置站有一位成员。乐团共有 `9` 种乐器，乐器编号为 `1~9`，每位成员持有 `1` 个乐器。

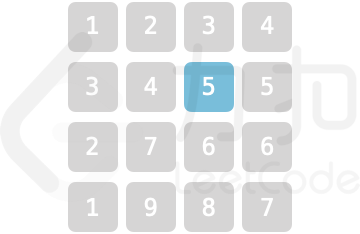
为保证声乐混合效果，成员站位规则为：自 grid 左上角开始顺时针螺旋形向内循环以 1，2，...，9 循环重复排列。例如当 num = 5 时，站位如图所示

请返回位于场地坐标 [Xpos,Ypos] 的成员所持乐器编号。

示例 1：

输入：num = 3, Xpos = 0, Ypos = 2

输出：3

解释：

示例 2：

输入：num = 4, Xpos = 1, Ypos = 2

输出：5

解释：

提示：

• 1 <= num <= 10^9
• 0 <= Xpos, Ypos < num

通过代码

高赞题解

思路：
1.获取所求点在第几层（此处根据所求点的位置，层数k可能会多算一层）
2.前第0，1...k层的数量和 与 所求点相对第k层左上角元素(第k层的入口元素)的相对路径做+或-运算，求得所求点的绝对路径（从起始点到所求点经过的长度）

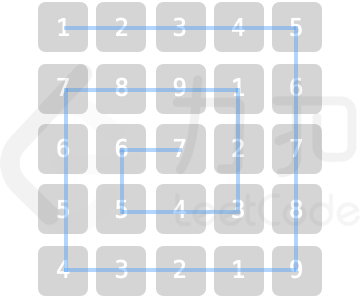
记：k(0,1,2...⌈n/2⌉ (往上取整))
C(k)=第k层的方块数目,如图C(0)=16,C(1)=8,C(2)=1;
T(k)=第k层以外（不包括第k层）的方块 数目，如图T(0)=0,T(1)=C(0)=16,T(2)=C(0)+C(1)=16+8=24,T(3)=16+8+1=25;
但是具体怎么计算呢 可以用补集的思想
T(k)=n*n-(n-2k)*(n-2k)=4*k*(n-k)

但是怎么求(i,j)点所在层 已经遍历过的数目呢 。(即下图深蓝色的路径长度)
1.求所在的层数k
k=min(x,n-1-x,y,n-1-y)(后续由于要分类讨论，k的求取可以直接通过其中某两个值求最小值即可); 即看该点距离哪个边界更近，所求的最小值就是第几层，如图 k=min(2,2,3,1),即处于第一层。那么我们也就知道了该层以外的橙色数目T(k)=T(1)=16。
2.求所求点(x,y)相对该层左上角点的相对路径长度

2.1 对于x<=y，我们可以知道dl=(x-k)+(y-k)+1
故 绝对路径长度为 T(k)+dl

2.2 但是对于x>y呢
如果我们采用相同的方法，就会导致对称的两个(i,j)与(j,i)相对路径相同。故才用另外一种方法
在计算层数k的时候 多计算一层，再从下一层的入口处回退dl个路径
此时绝对路径长度为 T(k+1)-dl ,注意dl计算时，仍用其真正所处的层数k'-1=(k+1)-1=k来计算。即：dl=(x-(k'-1))+(y-(k'-1))-1

(至于为何此处可直接-dl，可以看下图，下一层的入口点与上一层的入口点是右下和左上关系，按照螺旋顺序到(i,j)点的路径长度是相同的。)

最后， 就是把相应的路径长度len转化为1-9的数字即可，index=(len-1)%9+1。

当然此题也可拓展到m*n型的矩阵，最后一圈应该是一条线。n*n可以看作是m*n的特例，对于n为奇数的情况，一条线压缩成了一个点。
（注：本题思路来自网络文章，非原创，聊作整理，供大家交流学习）

[]
class Solution {
public:
    int orchestraLayout(int num, int xPos, int yPos) {
        long long x=xPos,y=yPos,n=num;
        if  (x <= y) {
            long long  k= min(x, n-1-y);
            return  (4*k*(n-k)+1+(x+y-k*2)-1)%9+1;
        }
        long long  kp =min(y, n-1-x)+1 ; 
        return   (4*kp*(n-kp)+1-(x+y-(kp-1)*2)-1)%9+1;
    }
};

[]
class Solution(object):
    def orchestraLayout(self, n, x, y):
        if  x <= y :
            k= min(x, n-1-y)
            return  (4*k*(n-k)+1+(x+y-k*2)-1)%9+1
        kp =min(y, n-1-x)+1 
        return  (4*kp*(n-kp)+1-(x+y-(kp-1)*2)-1)%9+1

统计信息

通过次数	提交次数	AC比率
5488	28744	19.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言