原文链接: https://leetcode-cn.com/problems/grid-illumination

英文原文

There is a 2D grid of size n x n where each cell of this grid has a lamp that is initially turned off.

You are given a 2D array of lamp positions lamps, where lamps[i] = [rowi, coli] indicates that the lamp at grid[rowi][coli] is turned on. Even if the same lamp is listed more than once, it is turned on.

When a lamp is turned on, it illuminates its cell and all other cells in the same row, column, or diagonal.

You are also given another 2D array queries, where queries[j] = [rowj, colj]. For the jth query, determine whether grid[rowj][colj] is illuminated or not. After answering the jth query, turn off the lamp at grid[rowj][colj] and its 8 adjacent lamps if they exist. A lamp is adjacent if its cell shares either a side or corner with grid[rowj][colj].

Return an array of integers ans, where ans[j] should be 1 if the cell in the jth query was illuminated, or 0 if the lamp was not.

 

Example 1:

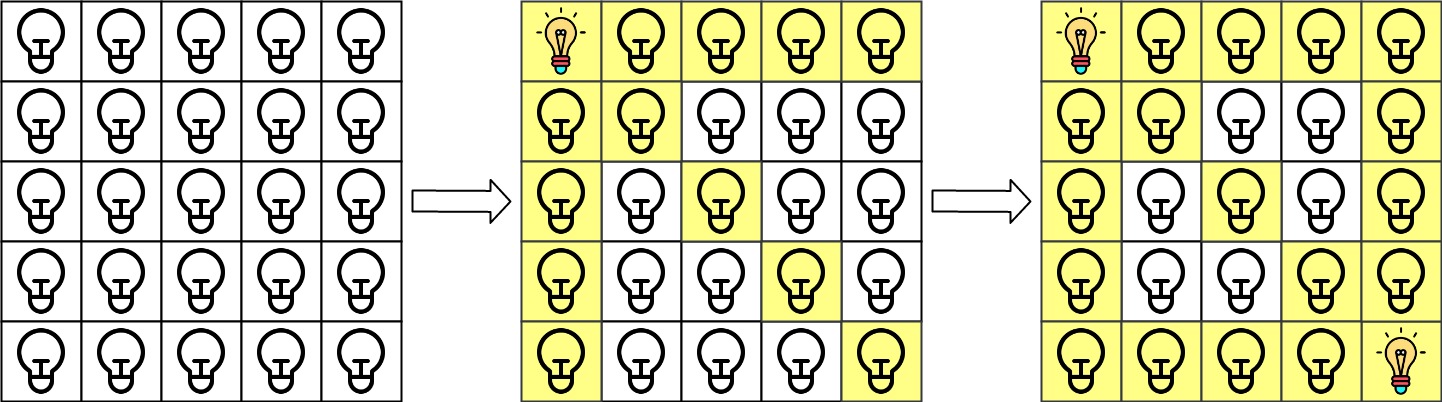
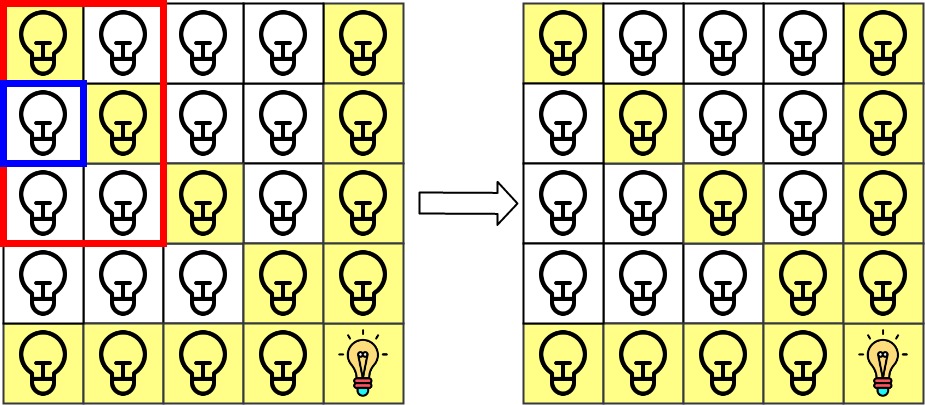
Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
Output: [1,0]
Explanation: We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid[0][0] then turning on the lamp at grid[4][4].
The 0th query asks if the lamp at grid[1][1] is illuminated or not (the blue square). It is illuminated, so set ans[0] = 1. Then, we turn off all lamps in the red square.

The 1st query asks if the lamp at grid[1][0] is illuminated or not (the blue square). It is not illuminated, so set ans[1] = 0. Then, we turn off all lamps in the red rectangle.

Example 2:

Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
Output: [1,1]

Example 3:

Input: n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
Output: [1,1,0]

 

Constraints:

• 1 <= n <= 109
• 0 <= lamps.length <= 20000
• 0 <= queries.length <= 20000
• lamps[i].length == 2
• 0 <= rowi, coli < n
• queries[j].length == 2
• 0 <= rowj, colj < n

中文题目

在 N x N 的网格 grid 上，每个单元格都有一盏灯，最初灯都处于 关闭 状态。

数组 lamps 表示打开的灯的位置。lamps[i] = [rowi, coli] 表示 打开 位于 grid[rowi][coli] 的第 i 盏灯 。每盏灯都照亮自身单元格以及同一行、同一列和两条对角线上的所有其他单元格。

查询数组 queries 中，第 i 次查询 queries[i] = [rowi, coli]，如果单元格 [rowi, coli] 是被照亮的，则查询结果为 1 ，否则为 0 。在第 i 次查询之后 [按照查询的顺序] ，关闭 位于单元格 grid[rowi][coli] 上或其相邻 8 个方向上（与单元格 grid[rowi][coli] 共享角或边）的任何灯。

返回答案数组 ans ， answer[i] 应等于第 i 次查询 queries[i] 的结果，1 表示照亮，0 表示未照亮。

 

示例 1：

输入：N = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
输出：[1,0]
解释：最初所有灯都是关闭的。在执行查询之前，打开位于 [0, 0] 和 [4, 4] 的灯。第 0 次查询检查 grid[1][1] 是否被照亮（蓝色方框）。该单元格被照亮，所以 ans[0] = 1 。然后，关闭红色方框中的所有灯。

第 1 次查询检查 grid[1][0] 是否被照亮（蓝色方框）。该单元格没有被照亮，所以 ans[1] = 0 。然后，关闭红色矩形中的所有灯。

示例 2：

输入：N = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
输出：[1,1]

示例 3：

输入：N = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
输出：[1,1,0]

 

提示：

• 1 <= N <= 109
• 0 <= lamps.length <= 20000
• lamps[i].length == 2
• 0 <= lamps[i][j] < N
• 0 <= queries.length <= 20000
• queries[i].length == 2
• 0 <= queries[i][j] < N

通过代码

高赞题解

草稿

思路

就如草稿中打的那样，我觉得每一个灯点亮的时候，它都会影响“整行”，“整列”，“正对角线”，“反对角线”。

如果两个灯在一行，我们显而易见可以得知这一行一定会被点亮。同时我们知道，如果我们熄灭其中一盏灯，这一行依旧充满光明！因为还有另一盏灯依然坚挺！只有当两盏灯同时熄灭，这一行才会重新回归黑暗。但是被熄灭的灯所处的列以及对角线波及到的区域，都会在它熄灭的同时，也陷入黑暗。

这让我们可以进行第一次抽象，看成每一盏灯的点亮都会对波及到的格子进行“计数+1”。而每一盏灯的熄灭都会对波及到的格子进行“计数-1”。

这样，如图，两盏同一行的灯，所处的行的计数就会变成2。这意味着，只有当两盏灯同时熄灭，才能让这一行的计数变成0（也就是变黑）。

但是问题来了，题目中给出的N的大小最大是10的九次方。显然，不可能开辟一个足够大的数组空间可供挥霍（时间也不允许）。

接下来，于是就如开头草稿中写的，我们可以设计四个记录器。之所以设计记录器是因为，每点亮一个灯，就必然会点亮“一行”，“一列”，“一个正对角线”，“一个反对角线”。我们不再需要去记录每一个格子的“光源亮度”。

我们查看一个格子的光源亮度，也只需要去看“这一行是否被点亮”，“这一列是否被点亮”，“这一个正对角线是否被点亮”…只要这些条件中，任一一个满足，就说明这个格子是被点亮的。

行记录器的索引和列记录器的索引是非常好确定的，可以直接等于所处格子的横纵坐标。

而正反对角线记录器的索引确定方式，我写在了草稿中。

至于最终记录器的实现方式，最开始想当然的使用了数组（草稿中也列出了数组的大小）…但忽略了题目N的给定范围，最终使用HashMap实现了记录器。

class Solution {

    //四个记录器

    HashMap<Integer, Integer> colRecorder;

    HashMap<Integer, Integer> rowRecorder;

    HashMap<Integer, Integer> positiveRecorder;

    HashMap<Integer, Integer> negetiveRecorder;



    //一个灯光记录器

    HashMap<Integer, Integer> lampsRecorder;



    //初始化方向向量

    private int[] dy = {-1, -1, -1, 0, 0, 0, 1, 1, 1};

    private int[] dx = {-1, 0, 1, -1, 0, 1, -1, 0, 1};

    private int directionLen = 9;



    private int N;



    public int[] gridIllumination(int N, int[][] lamps, int[][] queries) {

        //...

    }



    private int getPositiveIndex(int y, int x) {

        return x + y;

    }



    private int getNegetiveIndex(int y, int x) {

        return y - x + N - 1;

    }

}

统计信息

通过次数	提交次数	AC比率
2221	7475	29.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
N 皇后	困难