1203-项目管理(Sort Items by Groups Respecting Dependencies)
发表于：2021-12-03 | 分类： 困难
字数统计: 645 | 阅读时长: 3分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/sort-items-by-groups-respecting-dependencies

英文原文

There are n items each belonging to zero or one of m groups where group[i] is the group that the i-th item belongs to and it's equal to -1 if the i-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.

Return a sorted list of the items such that:

  • The items that belong to the same group are next to each other in the sorted list.
  • There are some relations between these items where beforeItems[i] is a list containing all the items that should come before the i-th item in the sorted array (to the left of the i-th item).

Return any solution if there is more than one solution and return an empty list if there is no solution.

 

Example 1:

Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
Output: [6,3,4,1,5,2,0,7]

Example 2:

Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
Output: []
Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list.

 

Constraints:

  • 1 <= m <= n <= 3 * 104
  • group.length == beforeItems.length == n
  • -1 <= group[i] <= m - 1
  • 0 <= beforeItems[i].length <= n - 1
  • 0 <= beforeItems[i][j] <= n - 1
  • i != beforeItems[i][j]
  • beforeItems[i] does not contain duplicates elements.

中文题目

有 n 个项目，每个项目或者不属于任何小组，或者属于 m 个小组之一。group[i] 表示第 i 个项目所属的小组，如果第 i 个项目不属于任何小组，则 group[i] 等于 -1。项目和小组都是从零开始编号的。可能存在小组不负责任何项目，即没有任何项目属于这个小组。

请你帮忙按要求安排这些项目的进度，并返回排序后的项目列表：

  • 同一小组的项目，排序后在列表中彼此相邻。
  • 项目之间存在一定的依赖关系，我们用一个列表 beforeItems 来表示，其中 beforeItems[i] 表示在进行第 i 个项目前（位于第 i 个项目左侧）应该完成的所有项目。

如果存在多个解决方案，只需要返回其中任意一个即可。如果没有合适的解决方案，就请返回一个 空列表 。

 

示例 1：

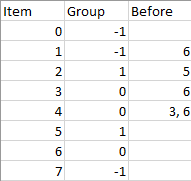
输入：n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
输出：[6,3,4,1,5,2,0,7]

示例 2：

输入：n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
输出：[]
解释：与示例 1 大致相同，但是在排序后的列表中，4 必须放在 6 的前面。

 

提示：

  • 1 <= m <= n <= 3 * 104
  • group.length == beforeItems.length == n
  • -1 <= group[i] <= m - 1
  • 0 <= beforeItems[i].length <= n - 1
  • 0 <= beforeItems[i][j] <= n - 1
  • i != beforeItems[i][j]
  • beforeItems[i] 不含重复元素

通过代码

官方题解

📺 视频讲解

视频时间线：

  • 解读题意：00:10
  • 拓扑排序简介：03:36
  • 示例 1 分析：07:50
  • 编码前的思路分析：09:59
  • 参考代码：12:18
  • 复杂度分析、练习：21:22

力扣君温馨小贴士：

  • 觉得视频时间长的扣友，可以在视频右下角的「设置」按钮处选择 1.5 倍速或者 2 倍速观看；
  • 如果已经充分了解了题意，对「拓扑排序」这个知识点已经非常熟悉的朋友，可以直接观看「编码前的思路分析」（09:59 开始）。

1203 项目管理.mp4

📖 文字解析

这个问题标注为「困难」，但是解决这个问题用到的知识点其实大家都见过。要点和提示如下：

  1. 从问题的描述（任务计划安排）和结果要求（有可能不存在，如果有，可能不唯一），可以看出思路是「拓扑排序」；
  2. 读懂题目的意思，这一点非常重要，弄清楚输入的每一个变量的含义，弄清楚什么叫「无人接手」以及 group[i] = - 1 的含义；
  3. 安排任务的第一优先级：组（group）相同的项目必须排在一起，第二优先级：项目（item）的先后顺序满足拓扑序；
  4. 关键 1：题目给出的 item 和 beforItem 可以得到 item 须要满足的先后顺序。而每一个 item 或者对应一个 group，或者不属于任何一个给定的 group，根据 item 和 group 的函数关系（从 item 可以得到唯一的 group 编号）：可以得到安排组（group）的先后顺序（这一点很关键）；
  5. 关键 2：分别对 group 和 item 执行拓扑排序，从 item -> group 的（多对一关系）反向得到 group -> item 的一对多关系，由于 item 按照拓扑序排列，建立 group 到 item 的一对多关系以后，每一个 group 对应的 item 列表是符合拓扑序的；
  6. 从 group 的拓扑序，和 group 到 item 的一对多关系，得到的 item 列表就是满足题目意思的一个结果。

下面是详解。

方法：拓扑排序

1. 如何得到组 group 的先后关系

  • 如果不考虑「同一小组的项目，排序后在列表中彼此相邻」。根据 beforeItems 可以得到项目 item 的拓扑排序结果；
  • 由数组 group 可以得到项目 item 对应的组的编号。

由以上两点，可以得到 组 group 的先后关系。

以示例 1 为例：

img

表格第 2 行（不计算表头）：项目 6 （组号 0）必需在项目 1 （不属于任何组，暂时记组号为 2）的前面，可以得出：组号为 0 的所有项目应该位于组号为 2 的所有项目的前面。

有可能出现这种情况：前驱项目和当前项目分在一组，这样的数据需要舍弃，例如第 5 行。项目 3 、项目 6 必需被安排在项目 4 的前面，但是它们的组号都为 0。

2. 如何让相同组号的项目在一起

由上一步的结果得到「组的先后关系」，进而得到组 group 的拓扑排序结果。而 同组的项目也必须满足先后顺序，因此必需对项目 item 也执行一次拓扑排序。

按照项目 item 的拓扑排序结果，依次 把它们映射到对应的组 group 里，这一步需要建立一个映射关系：key 是组编号，value 是同一组的项目按照拓扑排序的结果。

再根据组 group 的拓扑排序的结果，以及上一步建立的映射关系，把 group 映射到 item 列表，就得到了题目要求的 ① 同组项目放在一起 ② 且项目之间还满足拓扑序的拓扑排序结果。

3. 细节：为什么须要给 group[i] = -1 的项目赋值为一个新的组号？

根据题意，group[i] = -1 表示编号为 i 的项目，不属于编号为 0 到 m - 1 的这 m 个组，换句话说，完成这些项目不需要协同合作。

又因为我们需要根据「组」的先后顺序得到「组的拓扑排序的结果」。为了避免我们设计的算法认为 group[i] = -1 的这些项目都在同一组，因此给 group[i] = -1 的这些组一个不同于 0 到 m - 1 的编号，从 m 开始逐个给每个项目编号即可。

参考代码：

[]
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Queue;

public class Solution {

    public int[] sortItems(int n, int m, int[] group, List<List<Integer>> beforeItems) {
        // 第 1 步：数据预处理，给没有归属于一个组的项目编上组号
        for (int i = 0; i < group.length; i++) {
            if (group[i] == -1) {
                group[i] = m;
                m++;
            }
        }

        // 第 2 步：实例化组和项目的邻接表
        List<Integer>[] groupAdj = new ArrayList[m];
        List<Integer>[] itemAdj = new ArrayList[n];
        for (int i = 0; i < m; i++) {
            groupAdj[i] = new ArrayList<>();
        }
        for (int i = 0; i < n; i++) {
            itemAdj[i] = new ArrayList<>();
        }

        // 第 3 步：建图和统计入度数组
        int[] groupsIndegree = new int[m];
        int[] itemsIndegree = new int[n];

        int len = group.length;
        for (int i = 0; i < len; i++) {
            int currentGroup = group[i];
            for (int beforeItem : beforeItems.get(i)) {
                int beforeGroup = group[beforeItem];
                if (beforeGroup != currentGroup) {
                    groupAdj[beforeGroup].add(currentGroup);
                    groupsIndegree[currentGroup]++;
                }
            }
        }

        for (int i = 0; i < n; i++) {
            for (Integer item : beforeItems.get(i)) {
                itemAdj[item].add(i);
                itemsIndegree[i]++;
            }
        }

        // 第 4 步：得到组和项目的拓扑排序结果
        List<Integer> groupsList = topologicalSort(groupAdj, groupsIndegree, m);
        if (groupsList.size() == 0) {
            return new int[0];
        }
        List<Integer> itemsList = topologicalSort(itemAdj, itemsIndegree, n);
        if (itemsList.size() == 0) {
            return new int[0];
        }

        // 第 5 步：根据项目的拓扑排序结果，项目到组的多对一关系，建立组到项目的一对多关系
        // key：组，value：在同一组的项目列表
        Map<Integer, List<Integer>> groups2Items = new HashMap<>();
        for (Integer item : itemsList) {
            groups2Items.computeIfAbsent(group[item], key -> new ArrayList<>()).add(item);
        }

        // 第 6 步：把组的拓扑排序结果替换成为项目的拓扑排序结果
        List<Integer> res = new ArrayList<>();
        for (Integer groupId : groupsList) {
            List<Integer> items = groups2Items.getOrDefault(groupId, new ArrayList<>());
            res.addAll(items);
        }
        return res.stream().mapToInt(Integer::valueOf).toArray();
    }

    private List<Integer> topologicalSort(List<Integer>[] adj, int[] inDegree, int n) {
        List<Integer> res = new ArrayList<>();
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            if (inDegree[i] == 0) {
                queue.offer(i);
            }
        }

        while (!queue.isEmpty()) {
            Integer front = queue.poll();
            res.add(front);
            for (int successor : adj[front]) {
                inDegree[successor]--;
                if (inDegree[successor] == 0) {
                    queue.offer(successor);
                }
            }
        }

        if (res.size() == n) {
            return res;
        }
        return new ArrayList<>();
    }
}

复杂度分析：

说明：这里为了表达严谨，时间复杂度和空间复杂度的描述比较理论化。大家未必须要深究。就当前这个问题而言，拓扑排序就是就是在图中进行一次广度优先遍历，时间复杂度为图的顶点数加边数，假设当前问题的图结构的顶点数为 $V$、边数为 $E$，可以简记时间复杂度为 $O(V + E)$。

  • 时间复杂度：$O(m + n^2 + E_{group} + E_{item} )$，这里 $n$ 是项目的总数，$m$ 是组的总数（把标记为 $-1$ 的组预处理以后，新的组的总数不会超过 $2m$）；

    • 对组的数据进行预处理 $O(m)$；
    • 构建组的邻接表 $O(m)$、项目的邻接表 $O(n^2)$，遍历 before，最极端情况下，第 $1$ 个顶点指向所有剩余 $n - 1$ 个顶点，第 $2$ 个顶点指向所有剩余 $n - 2$ 个顶点，……；
    • 构建组的入度数组 $O(m)$、项目入度数组 $O(n)$；
    • 执行组的拓扑排序$O(m + E_{group})$、项目的拓扑排序 $O(n + E_{item})$。这里用 $E_{group}$ 表示组的邻接表的边数， $E_{item}$ 表示项目的邻接表的边数；
    • 构建组到项目的一对多关系 $O(m + n)$；
    • 输出符合题目要求的结果 $O(m + n)$。

  • 空间复杂度：$O(m + n^2)$；

    • 组的邻接表 $O(m)$、项目的邻接表 $O(n^2)$；
    • 组的入度数组 $O(m)$、项目入度数组 $O(n)$；
    • 组到项目的一对多关系 $O(m + n)$；
    • 符合题目要求的结果 $O(m + n)$。

练习

  1. 「力扣」第 207 题：课程表（中等）；
  2. 「力扣」第 210 题：课程表 II（中等）；
  3. 「力扣」第 301 题：最小高度树（中等）；
  4. 「力扣」第 802 题：找到最终的安全状态（中等）；
  5. 「力扣」第 630 题：课程表 III（困难）；
  6. 「力扣」第 329 题：矩阵中的最长递增路径（困难）；
  7. 「力扣」第 1245 题：树的直径（中等）；
  8. 「力扣」第 444 题：序列重建（中等）；
  9. 「力扣」第 1136 题：平行课程（困难）；
  10. 「力扣」第 269 题：火星词典（困难）。

统计信息

通过次数 提交次数 AC比率
12257 19795 61.9%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
深度优先搜索 广度优先搜索 图 拓扑排序
上一篇:
1202-交换字符串中的元素(Smallest String With Swaps)
下一篇:
1895-最大的幻方(Largest Magic Square)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo