1210-穿过迷宫的最少移动次数(Minimum Moves to Reach Target with Rotations)

原文链接: https://leetcode-cn.com/problems/minimum-moves-to-reach-target-with-rotations

英文原文

In an n*n grid, there is a snake that spans 2 cells and starts moving from the top left corner at (0, 0) and (0, 1). The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at (n-1, n-2) and (n-1, n-1).

In one move the snake can:

Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from (r, c) and (r, c+1) to (r, c) and (r+1, c).
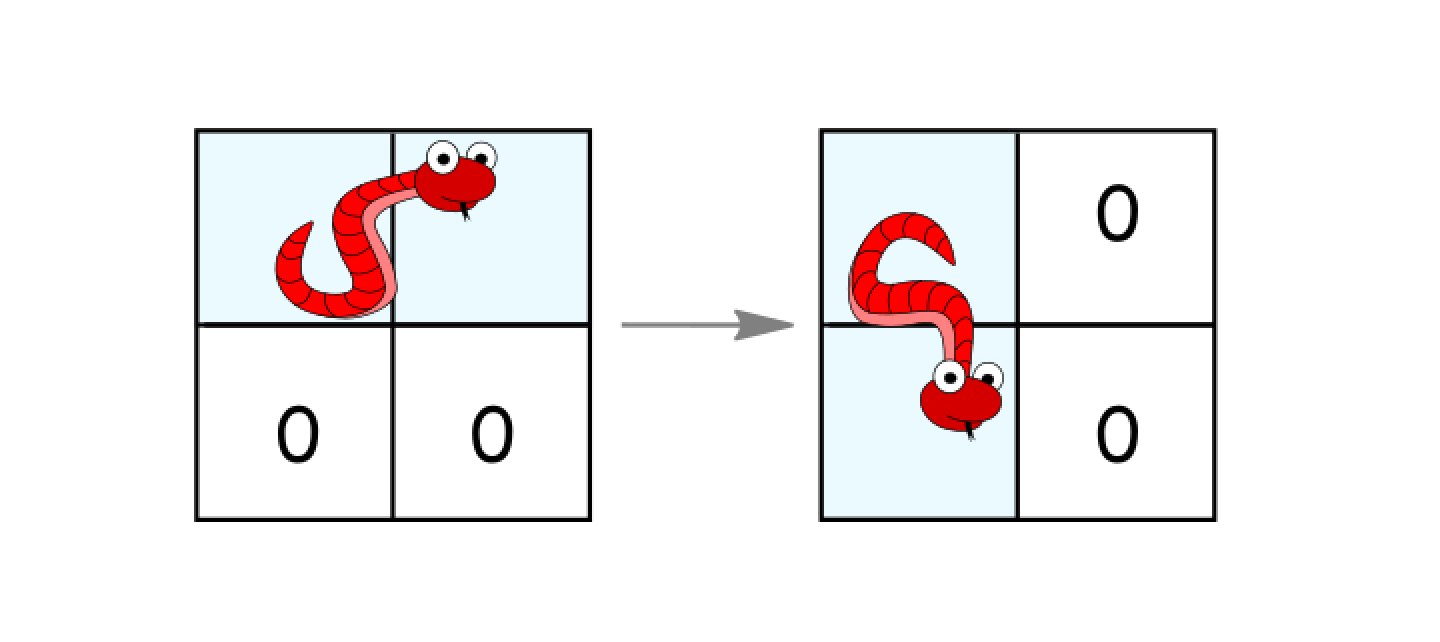
Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from (r, c) and (r+1, c) to (r, c) and (r, c+1).

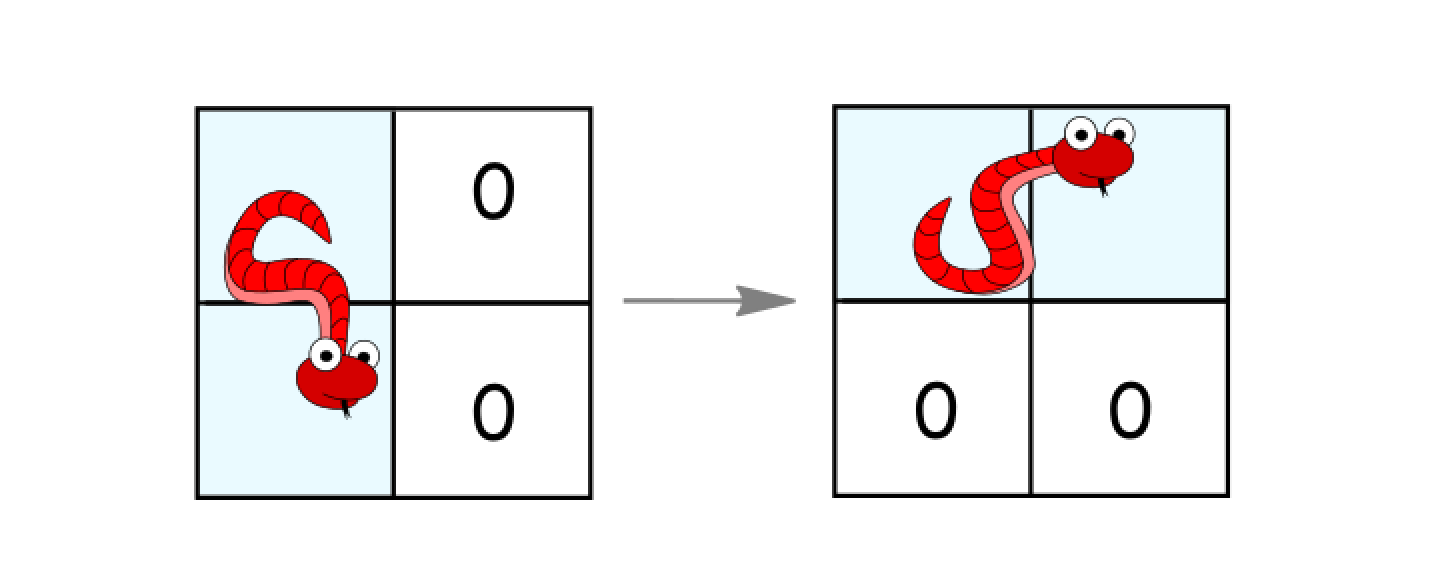
Return the minimum number of moves to reach the target.

If there is no way to reach the target, return -1.

Example 1:

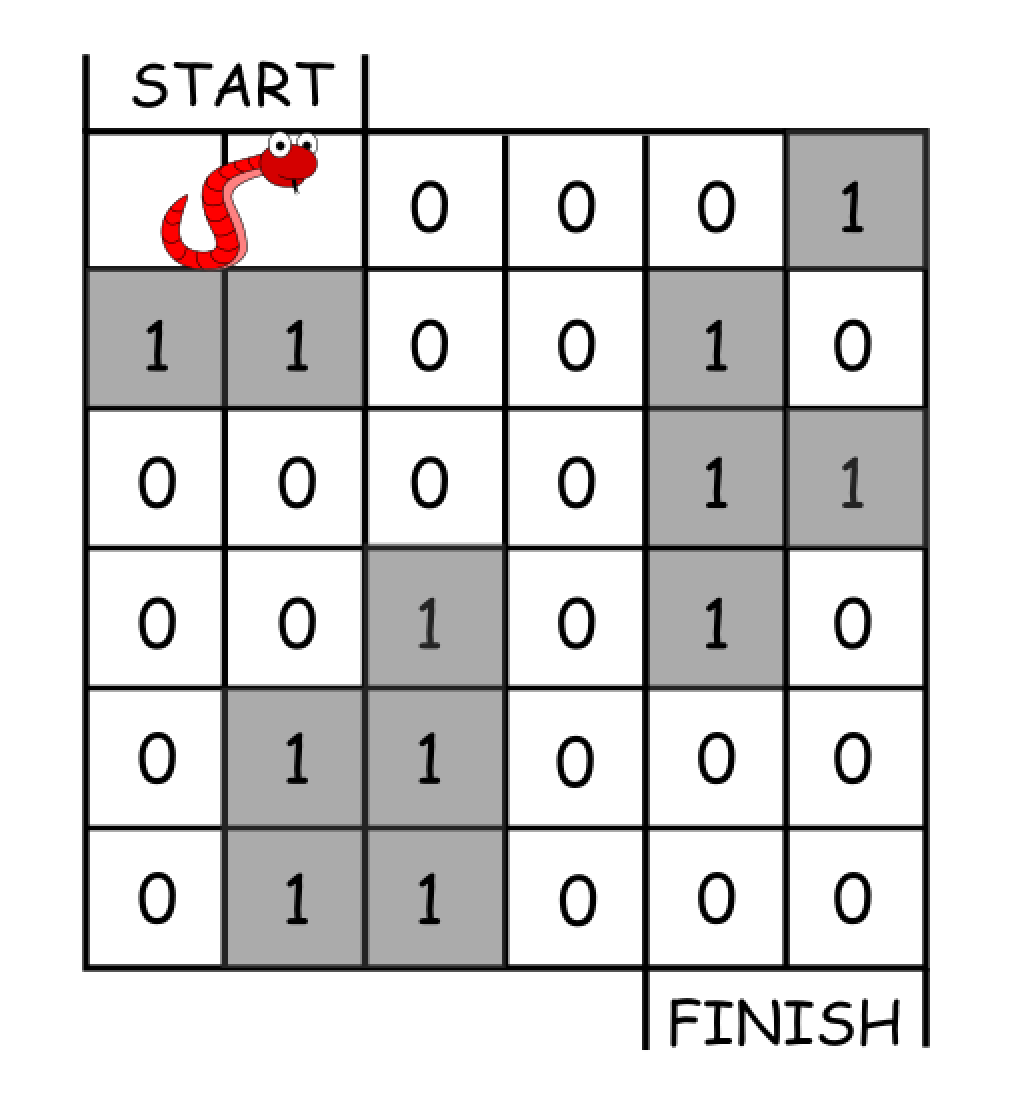
Input: grid = [[0,0,0,0,0,1],
               [1,1,0,0,1,0],
               [0,0,0,0,1,1],
               [0,0,1,0,1,0],
               [0,1,1,0,0,0],
               [0,1,1,0,0,0]]
Output: 11
Explanation:
One possible solution is [right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down].

Example 2:

Input: grid = [[0,0,1,1,1,1],
               [0,0,0,0,1,1],
               [1,1,0,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,0]]
Output: 9

Constraints:

2 <= n <= 100
0 <= grid[i][j] <= 1
It is guaranteed that the snake starts at empty cells.

中文题目

你还记得那条风靡全球的贪吃蛇吗？

我们在一个 n*n 的网格上构建了新的迷宫地图，蛇的长度为 2，也就是说它会占去两个单元格。蛇会从左上角（(0, 0) 和 (0, 1)）开始移动。我们用 0 表示空单元格，用 1 表示障碍物。蛇需要移动到迷宫的右下角（(n-1, n-2) 和 (n-1, n-1)）。

每次移动，蛇可以这样走：

如果没有障碍，则向右移动一个单元格。并仍然保持身体的水平／竖直状态。
如果没有障碍，则向下移动一个单元格。并仍然保持身体的水平／竖直状态。
如果它处于水平状态并且其下面的两个单元都是空的，就顺时针旋转 90 度。蛇从（(r, c)、(r, c+1)）移动到（(r, c)、(r+1, c)）。
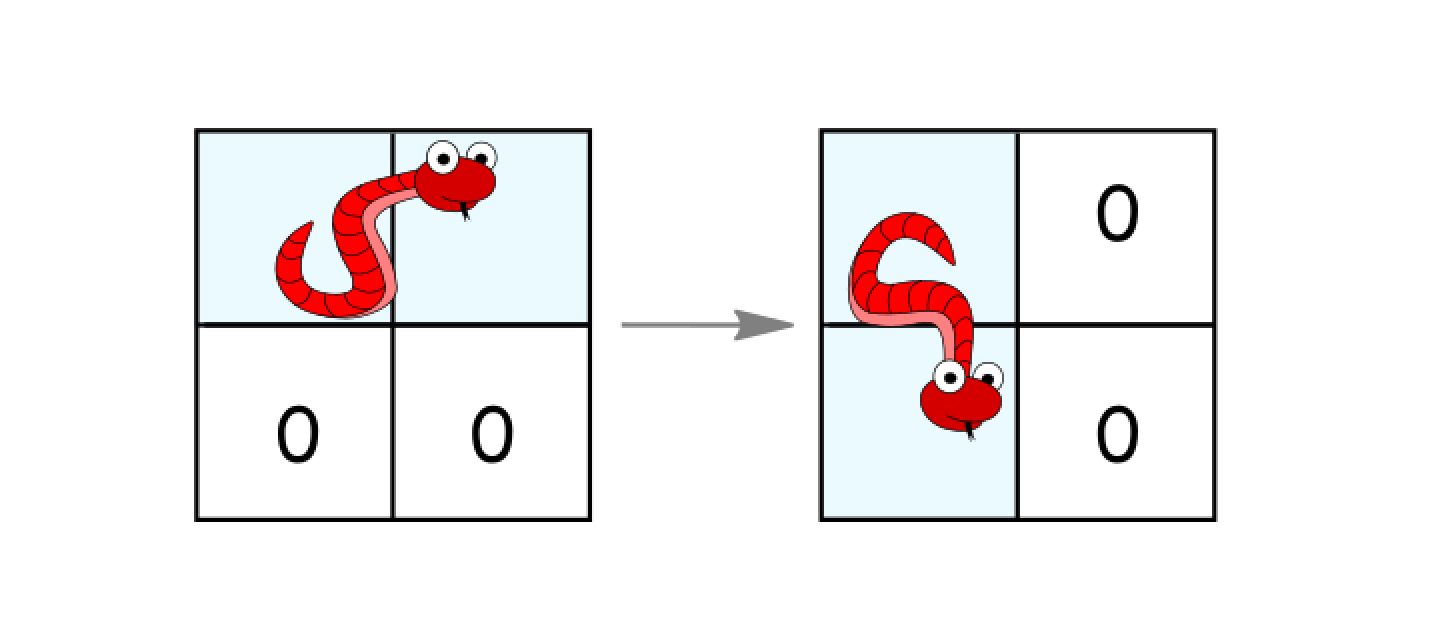
如果它处于竖直状态并且其右面的两个单元都是空的，就逆时针旋转 90 度。蛇从（(r, c)、(r+1, c)）移动到（(r, c)、(r, c+1)）。

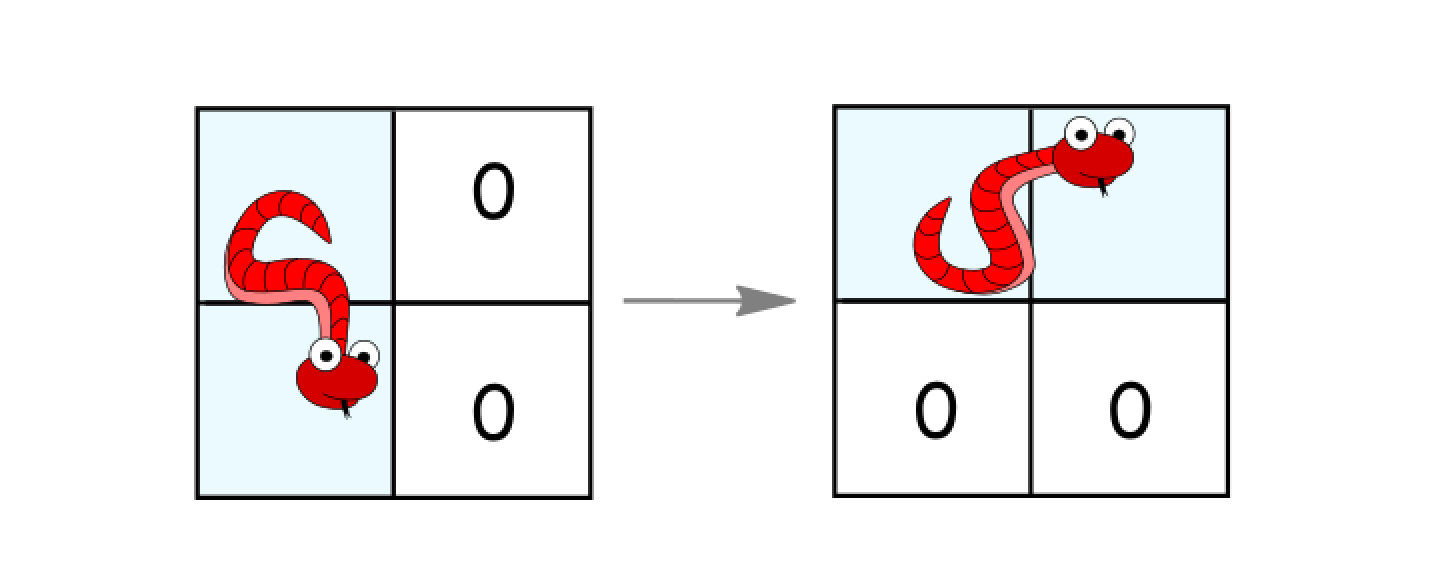
返回蛇抵达目的地所需的最少移动次数。

如果无法到达目的地，请返回 -1。

示例 1：

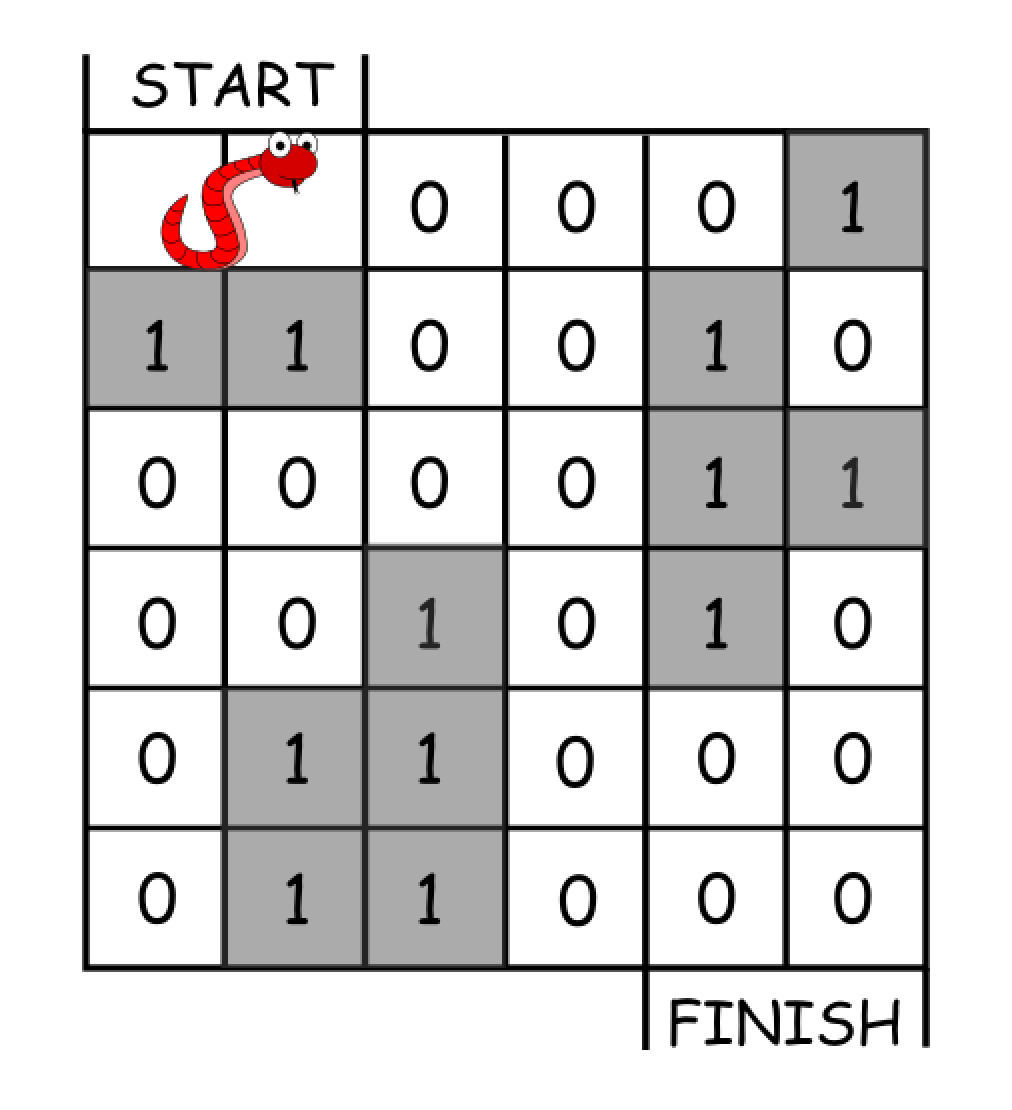
输入：grid = [[0,0,0,0,0,1],
               [1,1,0,0,1,0],
               [0,0,0,0,1,1],
               [0,0,1,0,1,0],
               [0,1,1,0,0,0],
               [0,1,1,0,0,0]]
输出：11
解释：
一种可能的解决方案是 [右, 右, 顺时针旋转, 右, 下, 下, 下, 下, 逆时针旋转, 右, 下]。

示例 2：

输入：grid = [[0,0,1,1,1,1],
               [0,0,0,0,1,1],
               [1,1,0,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,1],
               [1,1,1,0,0,0]]
输出：9

提示：

2 <= n <= 100
0 <= grid[i][j] <= 1
蛇保证从空单元格开始出发。

通过代码

高赞题解

解题思路：

看到最短路径，首先想到的就是 BFS，BFS 不行再考虑 DP。

那么我们先考虑 BFS，很显然，我们只要把蛇每次走位的坐标存到队列中，先进先出（FIFO），只要和目标坐标相等，即可返回。
我在这里没有存每个点的横坐标和纵坐标。通过一个值去计算两个坐标比如当前值为 8（表的大小为 m*n），横坐标 = 8%n, 纵坐标 = 8/n，假设当前位置是 (x1, x2)

那么蛇都有哪几种走位呢：

如果没有障碍，则向右移动一个单元格。并仍然保持身体的水平／竖直状态
因为题目说了仍然保持身体的水平/竖直状态，所以蛇在竖直状态也是可以向右平移
{:width=300} {:width=300}
我们不用刻意去考虑这两种状态只需要检查(x1 + 1)和(x2 + 1)是否有障碍物
如果没有障碍，则向下移动一个单元格。并仍然保持身体的水平／竖直状态
水平和竖直状态都是可以向下移动
{:width=300} {:width=300}
这里也不用刻意去考虑这两种状态只需要检查（x1 + n)和（x2 + n）是否有障碍物
如果它处于水平状态并且其下面的两个单元都是空的，就顺时针旋转 90 度
这里只有水平状态才可以移动
{:width=300}
通过图可以发现这种状态是检查（x1 + n）和（x2 + n）是否有障碍物，可以归到第 2 种状态中
如果它处于竖直状态并且其右面的两个单元都是空的，就逆时针旋转 90 度
{:width=300}
通过图可以发现这种状态是检查（x1 + 1）和（x2 + 1）是否有障碍物，可以归到第1种状态中

通过分析，我们只需要检查两种状态

如果（x1 + 1) 和 （x2 + 1) 没有障碍物，向右平移，如果是竖直状态，还可以旋转
如果（x1 + n) 和 （x2 + n) 没有障碍物，向下平移，如果是水平状态，还可以旋转

然后就是基本的 BFS 了，符合条件且没有访问过，加入到队列中，步数 +1，一直循环直到到达目的地或者队列为空。

代码：

[-Go]
func minimumMoves(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	visited := map[[2]int]bool{}
	targetX, targetY := m*n-2, m*n-1
	stack := [100000][3]int{}
	start, end := 0, 0
	stack[start] = [3]int{0, 1, 0}

	check := func(x, y, step int) bool {
		if x == targetX && y == targetY {
			return true
		}
		if visited[[2]int{x, y}] {
			return false
		}
		visited[[2]int{x, y}] = true
		end++
		stack[end] = [3]int{x, y, step + 1}
		return false
	}

	for start <= end {
		a, b, step := stack[start][0], stack[start][1], stack[start][2]
		start++
		x0, y0 := a/n, a%n
		x1, y1 := b/n, b%n
		// 向右
		if y0+1 < n && grid[x0][y0+1] == 0 && y1+1 < n && grid[x1][y1+1] == 0 {
			if check(n*x0+y0+1, n*x1+y1+1, step) {
				return step + 1
			}

			if y0 == y1 { // 竖直状态
				if check(a, n*x0+y0+1, step) {
					return step + 1
				}
			}
		}

		// 向下
		if x0+1 < m && grid[x0+1][y0] == 0 && x1+1 < m && grid[x1+1][y1] == 0 {
			if check(n*x0+y0+n, n*x1+y1+n, step) {
				return step + 1
			}

			if x0 == x1 { // 水平状态
				if check(a, n*x0+y0+n, step) {
					return step + 1
				}
			}
		}
	}
	return -1
}

统计信息

通过次数	提交次数	AC比率
2721	6027	45.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途