原文链接: https://leetcode-cn.com/problems/tiling-a-rectangle-with-the-fewest-squares

英文原文

Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.

 

Example 1:

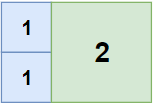
Input: n = 2, m = 3
Output: 3
Explanation: 3 squares are necessary to cover the rectangle.
2 (squares of 1x1)
1 (square of 2x2)

Example 2:

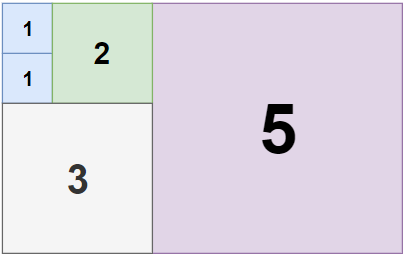
Input: n = 5, m = 8
Output: 5

Example 3:

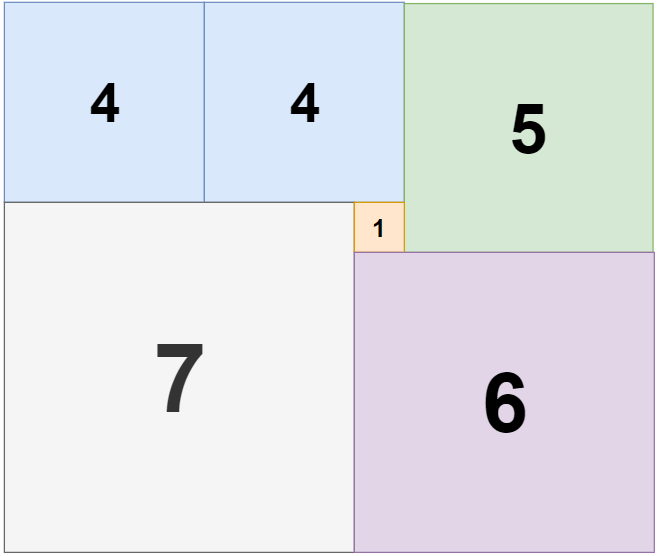
Input: n = 11, m = 13
Output: 6

 

Constraints:

• 1 <= n, m <= 13

中文题目

你是一位施工队的工长，根据设计师的要求准备为一套设计风格独特的房子进行室内装修。

房子的客厅大小为 n x m，为保持极简的风格，需要使用尽可能少的 正方形 瓷砖来铺盖地面。

假设正方形瓷砖的规格不限，边长都是整数。

请你帮设计师计算一下，最少需要用到多少块方形瓷砖？

 

示例 1：

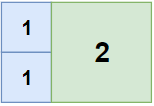
输入：n = 2, m = 3
输出：3
解释：3 块地砖就可以铺满卧室。
     2 块 1x1 地砖
     1 块 2x2 地砖

示例 2：

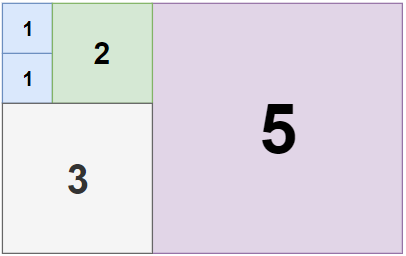
输入：n = 5, m = 8
输出：5

示例 3：

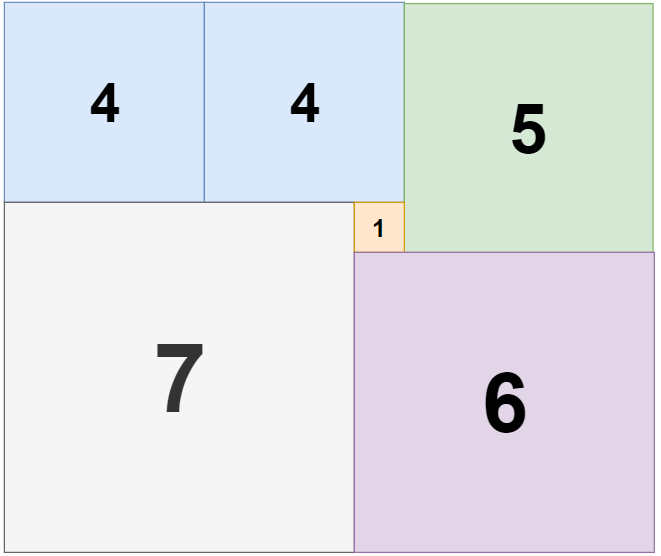
输入：n = 11, m = 13
输出：6

 

提示：

• 1 <= n <= 13
• 1 <= m <= 13

通过代码

高赞题解

此篇题解的思路搬运自参考文献1，感谢windede的分享
首先，完全背包问题是指：
有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的体积是ci，价值是wi。将哪些物品装入背包可使这些物品的体积总和不超过背包容量，且价值总和最大。
我们将完全背包问题的一种情况改写为：
有n种物品和一个容量为mn的背包，每种物品都有无限件可用。第i种物品的体积是ci^2，价值是1。将哪些物品装入背包可使这些物品的体积总和等于背包容量，且价值总和最小。
那么对于本题而言，不妨设m≥n，可以将mn的矩形看成是一个容量为mn的背包，有n种物品（边长为1到n的正方形），每种物品的体积为正方形边长的平方。可以看出，本题应该是强于上述改写的完全背包问题的（因为还需要考虑如何放置正方形，改写的完全背包问题只需要考虑总面积）。由于完全背包问题是NP完全问题，故此题不存在多项式时间解法。
此题正确的解法应该是dfs，找第一个没有被覆盖的方格，枚举正方形的边长进行暴力搜索求解。有个别可以优化的地方：f(kx,ky)=f(x,y);f(m+n,n)=f(m,n)+1(m≥n，实际上在数据大到一定情况下这个式子也是错的)。
更大规模的解法是建立0-1规划的模型，由参考文献2提出：用每个正方形的左下角坐标及边长表示一个正方形，最优化的目标是覆盖矩形所有方格所需的正方形数。由于我不会在这里编辑公式，请移步文献1或文献2观看。模型中优化目标有MN^2个0-1变量，限制条件有大约O(MN)个,规模相当巨大,可以考虑启发式算法。文献3中公布了380*380以内的计算结果，文献4给出了在线的可视化结果。
参考文献1：从矩阵谱分解到矩形的最少正方形剖分
参考文献2：Minimum tiling of a rectangle by squares
参考文献3：380*380以内的计算结果
参考文献4：380*380以内的可视化结果

统计信息

通过次数	提交次数	AC比率
2676	5402	49.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言