1289-下降路径最小和 II(Minimum Falling Path Sum II)

原文链接: https://leetcode-cn.com/problems/minimum-falling-path-sum-ii

英文原文

Given an n x n integer matrix grid, return the minimum sum of a falling path with non-zero shifts.

A falling path with non-zero shifts is a choice of exactly one element from each row of grid such that no two elements chosen in adjacent rows are in the same column.

Example 1:

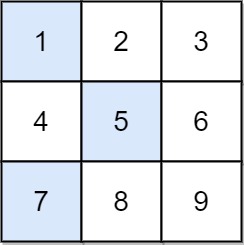
Input: arr = [[1,2,3],[4,5,6],[7,8,9]]
Output: 13
Explanation: 
The possible falling paths are:
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
The falling path with the smallest sum is [1,5,7], so the answer is 13.

Example 2:

Input: grid = [[7]]
Output: 7

Constraints:

n == grid.length == grid[i].length
1 <= n <= 200
-99 <= grid[i][j] <= 99

中文题目

给你一个整数方阵 arr ，定义「非零偏移下降路径」为：从 arr 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

请你返回非零偏移下降路径数字和的最小值。

示例 1：

输入：arr = [[1,2,3],[4,5,6],[7,8,9]]
输出：13
解释：
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。

提示：

1 <= arr.length == arr[i].length <= 200
-99 <= arr[i][j] <= 99

通过代码

高赞题解

前言

今天是我们讲解动态规划专题中的 路径问题的第六天。

我在文章结尾处列举了我所整理的关于 路径问题 的相关题目。

路径问题 我会按照编排好的顺序进行讲解（一天一道）。

你也先可以尝试做做，也欢迎你向我留言补充，你觉得与路径相关的 DP 类型题目 ~

动态规划

我们已经做过好几道「路径问题」了。

凭借我们的经验，一个直观的做法是定义 $f[i][j]$ 为到达位置 $(i,j)$ 的最小路径和。

那么答案必然是所有的 $f[n - 1][i]$ 中的最小值，i 的取值范围为 [0, n)。

代表最优路径的最后一个数可能取自最后一行的任意下标。

由于题目要求每一行的取数，不能与上一行的取数列下标相同。

也就是规定了我们为每行进行取数时不能取「正上方」的值。

因此我们在进行状态转移的时候，需要枚举上一行的所有列下标。

这样的做法复杂度是 $O(n^3)$，题目范围为 $10^2$，因此计算量为 $10^6$，可以过。

代码：

[]
class Solution {
    public int minFallingPathSum(int[][] arr) {
        int n = arr.length;
        int[][] f = new int[n][n];
        // 初始化首行的路径和
        for (int i = 0; i < n; i++) f[0][i] = arr[0][i];
        // 从第一行进行转移
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n; j++) {
                f[i][j] = Integer.MAX_VALUE;
                int val = arr[i][j];
                // 枚举上一行的每个列下标
                for (int p = 0; p < n; p++) {
                    // 只有列下标不同时，才能更新状态
                    if (j != p) {
                        f[i][j] = Math.min(f[i][j], f[i-1][p] + val);
                    }
                }
            }
        }
        // 在所有的 f[n - 1][i] 中取最小值
        int ans = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            ans = Math.min(ans, f[n-1][i]);
        }
        return ans;
    }
}

时间复杂度：$O(n^3)$
空间复杂度：$O(n^2)$

动态规划（进阶）

那么是否有比 $O(n^3)$ 更好的做法呢？

要知道我们上述的解法，当数据范围出到 $10^3$ 就会超时了。

我们来分析一下上述解法有哪些可优化的点：

1. DP 状态转移部分，共有 $n * n$ 个状态需要转移

2. 每次转移的时候，枚举上一行的所有列

我们要确保所有的方案都枚举到，得到的才是全局最优解。

因此 DP 部分，我们是无法优化的。

那就只剩下枚举上一行的所有列这个部分可以优化了。

其实细想就可以发现，当我们在计算某行的状态值的时候，只会用到「上一行」的两个值:最小值和次小值。

举个🌰，当我们已经处理完第 $i-1$ 行的状态值。

假设第 $i-1$ 行状态中的最小值对应的列下标是 $i1$，次小值对应的列下标是 $i2$。

那么当我们处理第 $i$ 行时，显然有：

处理第 $i$ 行中列下标为 $i1$ 的状态值时，由于不能选择「正上方」的数字，用到的是次小值。转移方程为：$f[i][j]=f[i-1][i2]+arr[i][j]$
处理第 $i$ 行其他列下标的状态值时，这时候用到的是最小值。转移方程为：$f[i][j]=f[i-1][i1]+arr[i][j]$

因此我们可以使用 i1 保存上一行的最小值对应的列下标，用 i2 保存次小值对应的列下标。

而无需每次转移都枚举上一行的所有列。

代码：

[]
class Solution {
    int MAX = Integer.MAX_VALUE;
    public int minFallingPathSum(int[][] arr) {
        int n = arr.length;
        int[][] f = new int[n][n];
        
        // i1 代表最小值列下标，i2 代表次小值列下标
        int i1 = -1, i2 = -1;
        
        // 先转移第一行
        for (int i = 0; i < n; i++) {
        
            // 更新动规值
            int val = arr[0][i];
            f[0][i] = val;
            
            // 更新 i1 和 i2
            if (val < (i1 == -1 ? MAX : f[0][i1])) {
                i2 = i1;
                i1 = i;
            } else if (val < (i2 == -1 ? MAX : f[0][i2])) {
                i2 = i;
            }
        }
        
        // 再转移剩余行
        for (int i = 1; i < n; i++) {
        
            // 当前转移第 i 行，使用临时变量保存转移过程中的「最小值列下标」&「次小值列下标」
            int ti1 = -1, ti2 = -1;
            
            for (int j = 0; j < n; j++) {
                f[i][j] = MAX;
                int val = arr[i][j];
                
                // 更新动规值
                // 可以选择「最小值」的列选择「最小值」
                if (j != i1) {
                    f[i][j] = f[i - 1][i1] + val;
                    
                // 不能选择「最小值」的列选择「次小值」
                } else {
                    f[i][j] = f[i - 1][i2] + val;
                }
                
                // 更新 ti1 和 ti2
                if (f[i][j] < (ti1 == -1 ? MAX : f[i][ti1])) {
                    ti2 = ti1;
                    ti1 = j;
                } else if (f[i][j] < (ti2 == -1 ? MAX : f[i][ti2])) {
                    ti2 = j;
                }
            }
            
            // 使用临时变量更新 i1 和 i2
            i1 = ti1; i2 = ti2;
        }
        int ans = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            ans = Math.min(ans, f[n-1][i]);
        }
        return ans;
    }
}

时间复杂度：$O(n^2)$
空间复杂度：$O(n^2)$

路径问题（目录）

62.不同路径（中等）：路径问题第一讲

63.不同路径 II（中等）：路径问题第二讲

64.最小路径和（中等）：路径问题第三讲

120.三角形最小路径和（中等）：路径问题第四讲

931.下降路径最小和（中等）：路径问题第五讲

1289.下降路径最小和 II（困难）：路径问题第六讲

1575.统计所有可行路径（困难）：路径问题第七讲（记忆化搜索）

1575.统计所有可行路径（困难）：路径问题第八讲（动态规划）

576.出界的路径数（中等）：路径问题第九讲

1301.最大得分的路径数目（困难）：路径问题第十讲

欢迎补充 ~

最后

如果有帮助到你，请给个点赞关注，让更多的人看到 ~ (“▔□▔)/

也欢迎你关注我和加入我们的「组队打卡」小群，提供写「证明」&「思路」的高质量题解

统计信息

通过次数	提交次数	AC比率
7266	11655	62.3%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途