原文链接: https://leetcode-cn.com/problems/minimum-number-of-taps-to-open-to-water-a-garden

英文原文

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e The length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

 

Example 1:

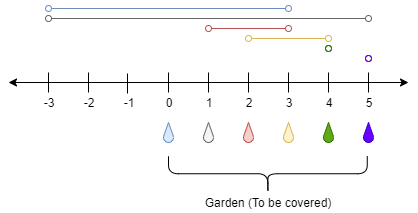
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

Example 3:

Input: n = 7, ranges = [1,2,1,0,2,1,0,1]
Output: 3

Example 4:

Input: n = 8, ranges = [4,0,0,0,0,0,0,0,4]
Output: 2

Example 5:

Input: n = 8, ranges = [4,0,0,0,4,0,0,0,4]
Output: 1

 

Constraints:

• 1 <= n <= 104
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

中文题目

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i -  ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

 

示例 1：

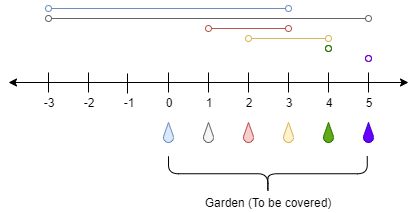
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。

示例 2：

输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。

示例 3：

输入：n = 7, ranges = [1,2,1,0,2,1,0,1]
输出：3

示例 4：

输入：n = 8, ranges = [4,0,0,0,0,0,0,0,4]
输出：2

示例 5：

输入：n = 8, ranges = [4,0,0,0,4,0,0,0,4]
输出：1

 

提示：

• 1 <= n <= 10^4
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

通过代码

高赞题解

解题思路：

1. n 代表土地数量（0 - 1 之间是一块地，1 - 2 之间是一块地）
2. n + 1 代表水龙头数量，水龙头插在数字上
3. ranges 代表当前位置的水龙头，向左向右可以覆盖多少块地
4. 定义一个 land 数据
   41. 代表在所有能够覆盖这块土地的所有水龙头中，找到能够覆盖最远（右边）位置的水龙头，记录它最右覆盖的土地
   42. 比如图例中，索引 0 代表覆盖了 0 - 1 之间这块地的所有水龙头里能够覆盖到最右的土地
   43. 值是 5 ，代表覆盖到最右边的是 4 - 5 这块土地

       索引是水龙头右边的那块地，而值是水龙头左边的那块地
       因此下面代码中 cur = land[cur]; 表示无缝的覆盖过去

5. 将 ranges 转换为 land 数据
   51. 遍历 ranges ，解析其范围，将范围内的 land 更新为最大值
6. 从土地 0 开始，一直到土地 n ，记录水龙头数目

代码：

[]
int minTaps(int n, vector<int>& ranges) 
{
	vector<int> land(n);
	for (int i = 0; i < ranges.size(); i++)
	{
		int l = max(i - ranges[i], 0);
		int r = min(i + ranges[i], n);
		for (int j = l; j < r; j++)
		{
			land[j] = max(land[j], r);
		}
	}

	int cnt = 0;
	int cur = 0;
	while (cur < n)
	{
		if (land[cur] == 0) return -1;
		cur = land[cur];
		cnt++;
	}
	return cnt;
}

---

致谢

感谢您的观看，希望对您有帮助，欢迎热烈的交流！

统计信息

通过次数	提交次数	AC比率
5985	12668	47.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言