原文链接: https://leetcode-cn.com/problems/jump-game-v

英文原文

Given an array of integers arr and an integer d. In one step you can jump from index i to index:

• i + x where: i + x < arr.length and 0 < x <= d.
• i - x where: i - x >= 0 and 0 < x <= d.

In addition, you can only jump from index i to index j if arr[i] > arr[j] and arr[i] > arr[k] for all indices k between i and j (More formally min(i, j) < k < max(i, j)).

You can choose any index of the array and start jumping. Return the maximum number of indices you can visit.

Notice that you can not jump outside of the array at any time.

 

Example 1:

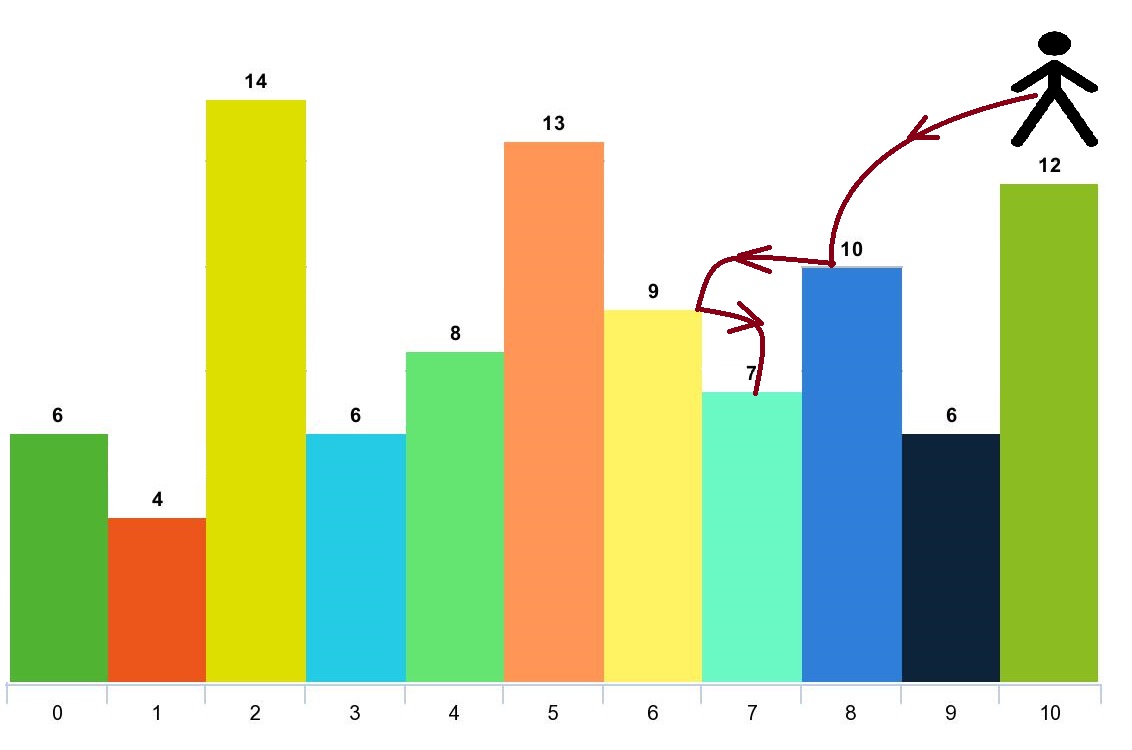
Input: arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
Output: 4
Explanation: You can start at index 10. You can jump 10 --> 8 --> 6 --> 7 as shown.
Note that if you start at index 6 you can only jump to index 7. You cannot jump to index 5 because 13 > 9. You cannot jump to index 4 because index 5 is between index 4 and 6 and 13 > 9.
Similarly You cannot jump from index 3 to index 2 or index 1.

Example 2:

Input: arr = [3,3,3,3,3], d = 3
Output: 1
Explanation: You can start at any index. You always cannot jump to any index.

Example 3:

Input: arr = [7,6,5,4,3,2,1], d = 1
Output: 7
Explanation: Start at index 0. You can visit all the indicies. 

Example 4:

Input: arr = [7,1,7,1,7,1], d = 2
Output: 2

Example 5:

Input: arr = [66], d = 1
Output: 1

 

Constraints:

• 1 <= arr.length <= 1000
• 1 <= arr[i] <= 10^5
• 1 <= d <= arr.length

中文题目

给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到：

• i + x ，其中 i + x < arr.length 且 0 < x <= d 。
• i - x ，其中 i - x >= 0 且 0 < x <= d 。

除此以外，你从下标 i 跳到下标 j 需要满足：arr[i] > arr[j] 且 arr[i] > arr[k] ，其中下标 k 是所有 i 到 j 之间的数字（更正式的，min(i, j) < k < max(i, j)）。

你可以选择数组的任意下标开始跳跃。请你返回你 最多 可以访问多少个下标。

请注意，任何时刻你都不能跳到数组的外面。

 

示例 1：

输入：arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
输出：4
解释：你可以从下标 10 出发，然后如上图依次经过 10 --> 8 --> 6 --> 7 。
注意，如果你从下标 6 开始，你只能跳到下标 7 处。你不能跳到下标 5 处因为 13 > 9 。你也不能跳到下标 4 处，因为下标 5 在下标 4 和 6 之间且 13 > 9 。
类似的，你不能从下标 3 处跳到下标 2 或者下标 1 处。

示例 2：

输入：arr = [3,3,3,3,3], d = 3
输出：1
解释：你可以从任意下标处开始且你永远无法跳到任何其他坐标。

示例 3：

输入：arr = [7,6,5,4,3,2,1], d = 1
输出：7
解释：从下标 0 处开始，你可以按照数值从大到小，访问所有的下标。

示例 4：

输入：arr = [7,1,7,1,7,1], d = 2
输出：2

示例 5：

输入：arr = [66], d = 1
输出：1

 

提示：

• 1 <= arr.length <= 1000
• 1 <= arr[i] <= 10^5
• 1 <= d <= arr.length

通过代码

高赞题解

这道题如果用暴力dfs 可能会卡在超时的边缘，因为如果计算每个点的最大步数的话，会产生大量的重复计算。

所以换个思路来讲，我们遍历每个点的顺序 从矮到高遍历，然后记录每个点的可移动的最大步数。

这样就可以得到的动态转移方程为
dp[i] = max(dp[可以去的阶梯])+1;

非常的简单粗暴而且社会

class Solution {
public:
	int maxJumps(vector<int>& arr, int d) {
		int n = arr.size();
		vector<vector<int>> temp;
		vector<int> dp(n, 0);
		int res = 1;
		for (int i = 0; i < arr.size(); i++)
			temp.push_back({ arr[i],i });
		sort(temp.begin(), temp.end());

		for (int i = 0; i < n; i++) {
			int index = temp[i][1]; //编号;
			dp[index] = 1;
			//向左找
			for (int j = index - 1; j >= index - d && j >= 0; j--) {
				if (arr[j] >= arr[index]) break;
				if (dp[j] != 0) dp[index] = max(dp[index], dp[j ] + 1);
			}
			//向右找
			for (int j = index + 1; j <= index + d && j < n; j++) {
				if (arr[j] >= arr[index]) break;
				if (dp[j] != 0) dp[index] = max(dp[index], dp[j] + 1);
			}
			res = max(dp[index], res);
		}
		return res;

	}
};

统计信息

通过次数	提交次数	AC比率
4572	7959	57.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言