原文链接: https://leetcode-cn.com/problems/maximum-sum-bst-in-binary-tree

英文原文

Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

 

Example 1:

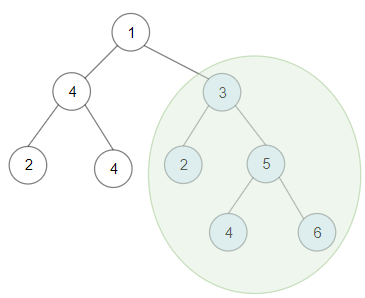
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

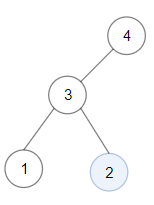
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Example 4:

Input: root = [2,1,3]
Output: 6

Example 5:

Input: root = [5,4,8,3,null,6,3]
Output: 7

 

Constraints:

• The number of nodes in the tree is in the range [1, 4 * 104].
• -4 * 104 <= Node.val <= 4 * 104

中文题目

给你一棵以 root 为根的 二叉树 ，请你返回 任意 二叉搜索子树的最大键值和。

二叉搜索树的定义如下：

• 任意节点的左子树中的键值都 小于 此节点的键值。
• 任意节点的右子树中的键值都 大于 此节点的键值。
• 任意节点的左子树和右子树都是二叉搜索树。

 

示例 1：

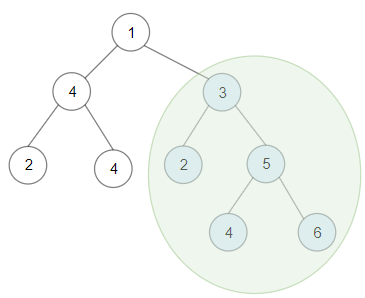
输入：root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
输出：20
解释：键值为 3 的子树是和最大的二叉搜索树。

示例 2：

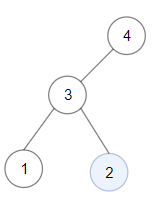
输入：root = [4,3,null,1,2]
输出：2
解释：键值为 2 的单节点子树是和最大的二叉搜索树。

示例 3：

输入：root = [-4,-2,-5]
输出：0
解释：所有节点键值都为负数，和最大的二叉搜索树为空。

示例 4：

输入：root = [2,1,3]
输出：6

示例 5：

输入：root = [5,4,8,3,null,6,3]
输出：7

 

提示：

• 每棵树有 1 到 40000 个节点。
• 每个节点的键值在 [-4 * 10^4 , 4 * 10^4] 之间。

通过代码

高赞题解

解题思路

比赛时ac的解答是错误的，用例[9,4,10,null,null,6,11]错误，已发布的大多数题解都有这个问题。
多谢评论区978007503@qq.com指正。

当前节点为根的树是不是二叉搜索树和几个状态有关

1. 左子树是不是二叉搜索树
2. 右子树是不是二叉搜索树
3. 当前val是不是大于左子树最大val
4. 当前val是不是小于右子树最小val

我们确定root节点为根的树是不是二叉搜索树，需要其左右子树处理时返回四个值

1. 子树是不是二叉搜索树 vec[0]
2. 子树的最小值 vec[1]
3. 子树的最大值 vec[2]
4. 子树的sum值 vec[3]

根据左右子节点返回值，构造当前节点的返回
当左右子树的任一vec[0]为false，或者当前val <= 左子vec[2] 或者val >= 右子vec[1]时返回 {false,随意，随意，随意}
如果判断当前树是搜索树，则返回 {true, 左子v[1], 右子v[2], val + 左子v[3] + 右子v[3]}
另外注意的是null的处理，我这里返回了{true, INT_MAX, INT_MIN, 0}。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxsum = 0;
    int maxSumBST(TreeNode* root) {
        dfs(root);
        return maxsum;
    }
    vector<int> dfs(TreeNode* root) {
        if (!root) return {true, INT_MAX, INT_MIN, 0};
        auto lArr = dfs(root->left);
        auto rArr = dfs(root->right);
        int sum = 0, curmax, curmin;
        if (!lArr[0] || !rArr[0] || root->val >= rArr[1] || root->val <= lArr[2]) {
            return {false, 0, 0, 0};
        }
        curmin = root->left ? lArr[1] : root->val;
        curmax = root->right ? rArr[2] : root->val;
        sum += (root->val + lArr[3] + rArr[3]);
        maxsum = max(maxsum, sum);
        return {true, curmin, curmax, sum};
    }
};

统计信息

通过次数	提交次数	AC比率
8540	21057	40.6%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言