英文原文
There is a pizza with 3n slices of varying size, you and your friends will take slices of pizza as follows:
- You will pick any pizza slice.
- Your friend Alice will pick next slice in anti clockwise direction of your pick.
- Your friend Bob will pick next slice in clockwise direction of your pick.
- Repeat until there are no more slices of pizzas.
Sizes of Pizza slices is represented by circular array slices in clockwise direction.
Return the maximum possible sum of slice sizes which you can have.
Example 1:
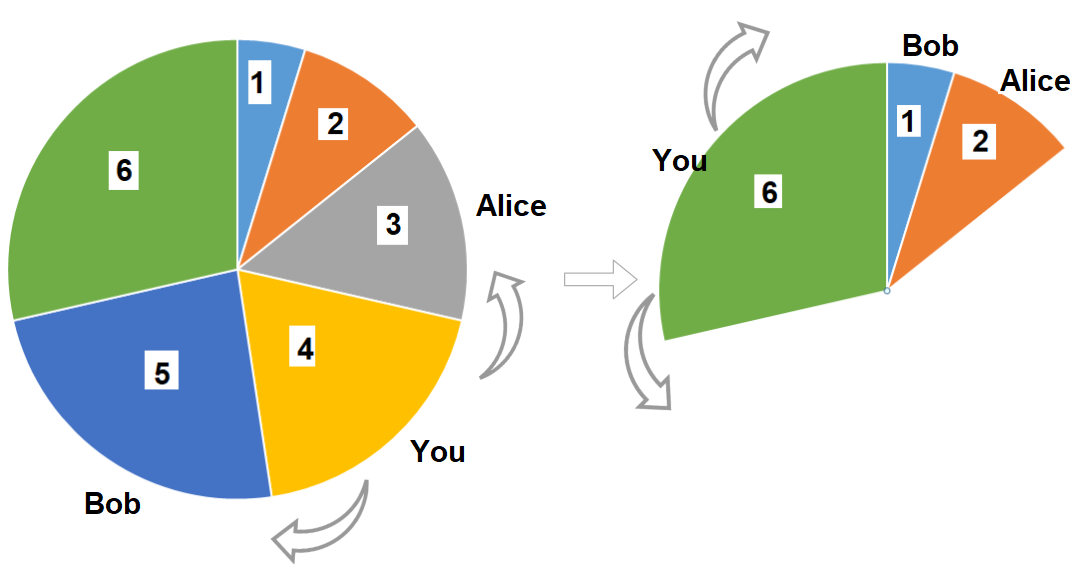
Input: slices = [1,2,3,4,5,6] Output: 10 Explanation: Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.
Example 2:
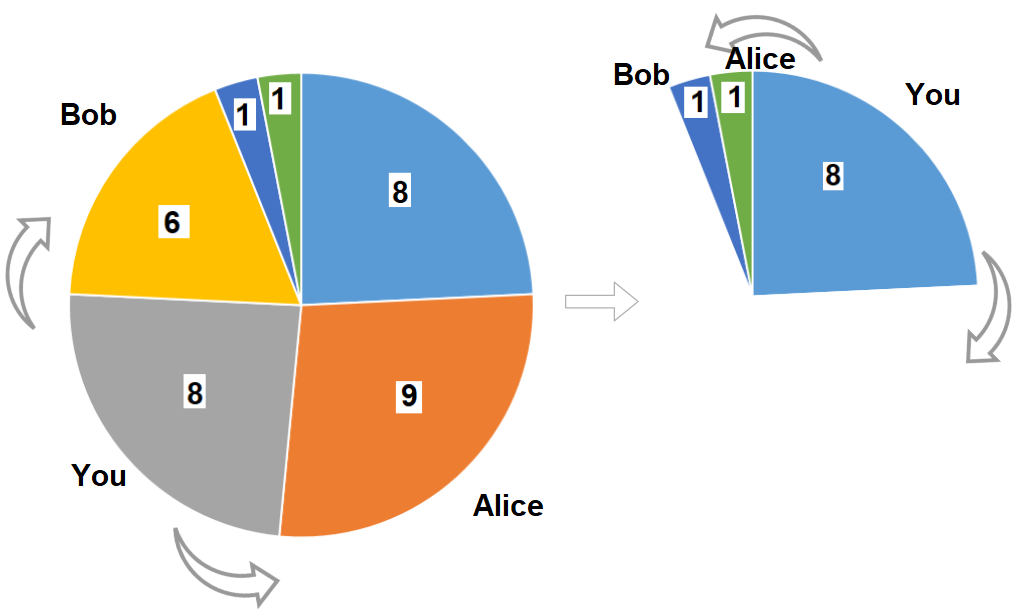
Input: slices = [8,9,8,6,1,1] Output: 16 Output: Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.
Example 3:
Input: slices = [4,1,2,5,8,3,1,9,7] Output: 21
Example 4:
Input: slices = [3,1,2] Output: 3
Constraints:
1 <= slices.length <= 500slices.length % 3 == 01 <= slices[i] <= 1000
中文题目
给你一个披萨,它由 3n 块不同大小的部分组成,现在你和你的朋友们需要按照如下规则来分披萨:
- 你挑选 任意 一块披萨。
- Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
- Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
- 重复上述过程直到没有披萨剩下。
每一块披萨的大小按顺时针方向由循环数组 slices 表示。
请你返回你可以获得的披萨大小总和的最大值。
示例 1:
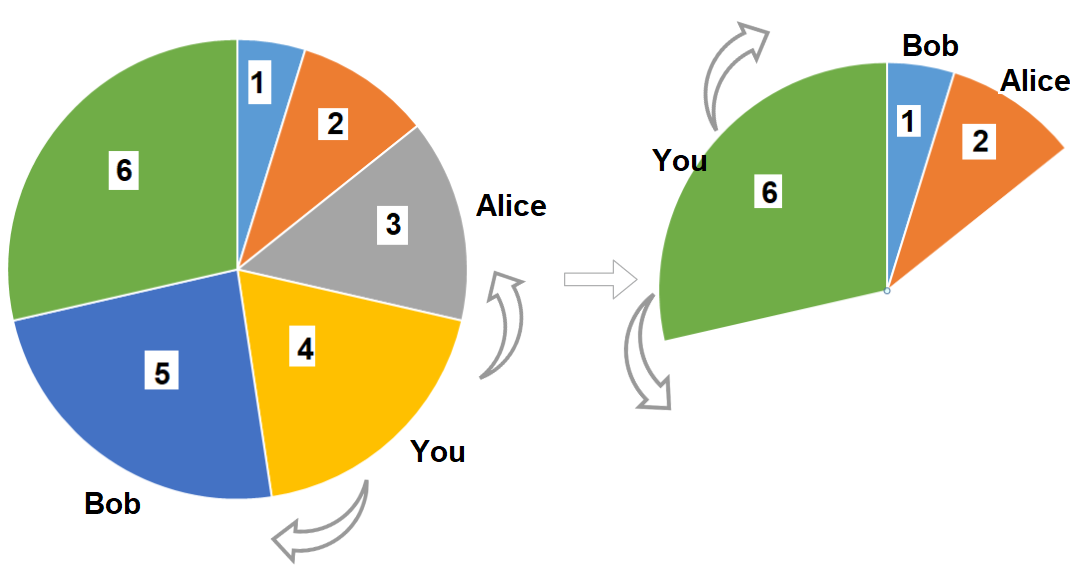
输入:slices = [1,2,3,4,5,6] 输出:10 解释:选择大小为 4 的披萨,Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨,Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。
示例 2:
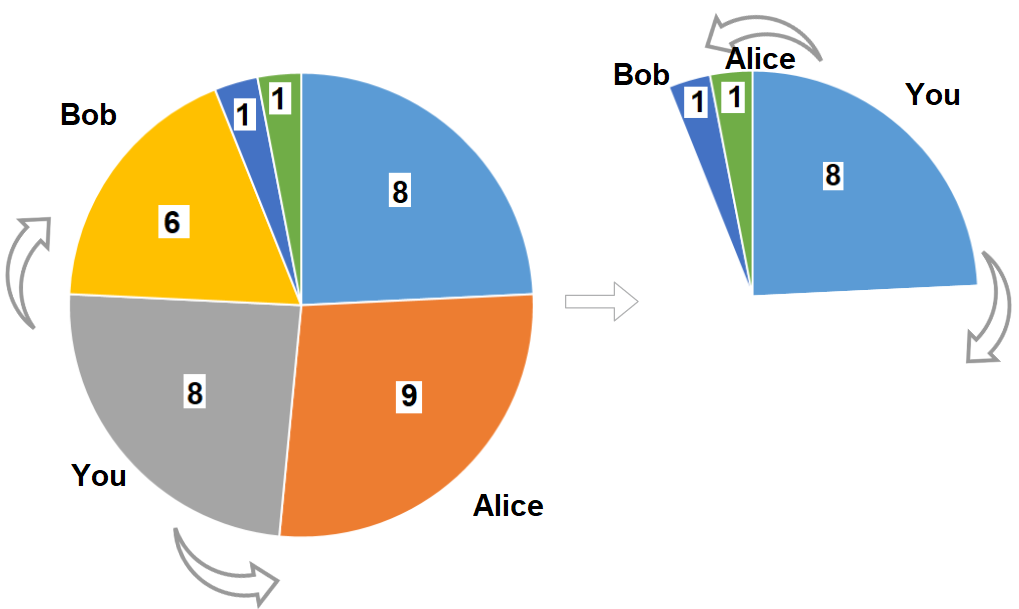
输入:slices = [8,9,8,6,1,1] 输出:16 解释:两轮都选大小为 8 的披萨。如果你选择大小为 9 的披萨,你的朋友们就会选择大小为 8 的披萨,这种情况下你的总和不是最大的。
示例 3:
输入:slices = [4,1,2,5,8,3,1,9,7] 输出:21
示例 4:
输入:slices = [3,1,2] 输出:3
提示:
1 <= slices.length <= 500slices.length % 3 == 01 <= slices[i] <= 1000
通过代码
高赞题解
解题思路
这道题目的难点其实在于如何将题意化简。如果我们考虑取披萨的顺序,由于每次取完后,披萨之间的相邻情况还会发生变化,算法的实现将变得非常复杂。试验几次之后,我们不难发现,如果选取的序号存在相邻的(包括首尾相邻),这种选取方式必然不成立;而如果序号都不相邻,似乎总能够找到一种方式取到这些序号。
那么,是不是只要不存在相邻的序号,就一定可以取到对应序号的元素呢?答案是肯定的。我们可以把要选取的元素跟它右边的元素绑定,这样总共就变成了$n/3$个单块的披萨,以及$n/3$个双块的披萨。每次,我们总可以找到一个左边有单块披萨的双块披萨,然后选取它。这样到最后,我们一定可以取到我们需要的$n/3$块披萨。
这样,问题就简化为:求在$n$个首尾相连的元素中,选取$n/3$个不相邻元素所能获得的最大值。
动态规划的方法很好理解,讨论区的其他题解也介绍得很清楚了。这里介绍一种时间复杂度更优的基于双向链表的贪心算法。
基于双向链表的贪心算法
这道题目中,直观想到的贪心策略是每一步选取最大的一块。但以$[8,9,8,1,2,3]$为例,如果我们第一步选取了$9$,剩下的元素就变成了$[1,2,3]$,我们最大只能选择$3$,这样的总和就只有$12$,而显然选取两个$8$可以得到$16$的总和,是更优的。
如果我们可以反悔就好了。问题是,怎么反悔?在上面的例子中,我们第一步选$9$之后,如果直接删除两个$8$,那就失去了反悔的机会,因为后面再也不会处理到它们了。所以,我们需要删除两个$8$对应的节点,同时保留它们的信息。信息保留在哪里?只能是$9$所对应的节点。
我们在选取$9$之后,将左右两个节点删除,同时将$9$修改为$8+8-9=7$,这样我们后面仍然有机会选到这个$7$,也就相当于反悔了对$9$的选择,而去选择了左右两边的两个$8$。
重复这样的操作,直到选取了$n/3$个元素为止,我们就得到了需要的最优解。
为什么我们的反悔操作一定是同时选择左右两个元素呢?因为我们是从大到小处理所有元素的,所以左右两边的元素一定不大于中间的元素,如果我们只选取其中的一个,是不可能得到更优解的。
实现
- 基于vector实现双向链表
- 基于优先队列获取当前最大值
复杂度分析
一共有$n+n/3$次入队操作,所以总的时间复杂度为$O(n\log n)$。
代码
struct Node {
int value, l, r;
};
vector<Node> a; // 基于vector实现双向链表
struct Id {
int id;
bool operator<(const Id &that) const {
return a[id].value < a[that.id].value;
}
};
void del(int i) {
// 这里不需要更新i的左右指针,因为i已经不会再被使用了
a[a[i].l].r = a[i].r;
a[a[i].r].l = a[i].l;
}
class Solution {
public:
int maxSizeSlices(vector<int> &slices) {
int n = slices.size();
int k = n / 3;
// 初始化双向链表
a.clear();
for (int i = 0; i < n; ++i)
a.emplace_back(Node{slices[i], (i - 1 + n) % n, (i + 1) % n});
priority_queue<Id> pq;
vector<bool> can_take(n, true); // 标记某一序号是否能够选取
int idx = 0;
for (int i = 0; i < n; ++i)
pq.push(Id{i}); // 优先队列初始化
int cnt = 0, ans = 0;
while (cnt < k) {
int id = pq.top().id;
pq.pop();
if (can_take[id]) { // 当前序号可用
cnt++;
ans += a[id].value;
// 标记前后序号
int pre = a[id].l;
int nxt = a[id].r;
can_take[pre] = false;
can_take[nxt] = false;
// 更新当前序号的值为反悔值
a[id].value = a[pre].value + a[nxt].value - a[id].value;
// 当前序号重新入队
pq.push(Id{id});
// 删除前后序号(更新双向链表)
del(pre);
del(nxt);
}
}
return ans;
}
};参考
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 4408 | 8096 | 54.4% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




