1444-切披萨的方案数(Number of Ways of Cutting a Pizza)

原文链接: https://leetcode-cn.com/problems/number-of-ways-of-cutting-a-pizza

英文原文

Given a rectangular pizza represented as a rows x cols matrix containing the following characters: 'A' (an apple) and '.' (empty cell) and given the integer k. You have to cut the pizza into k pieces using k-1 cuts.

For each cut you choose the direction: vertical or horizontal, then you choose a cut position at the cell boundary and cut the pizza into two pieces. If you cut the pizza vertically, give the left part of the pizza to a person. If you cut the pizza horizontally, give the upper part of the pizza to a person. Give the last piece of pizza to the last person.

Return the number of ways of cutting the pizza such that each piece contains at least one apple. Since the answer can be a huge number, return this modulo 10^9 + 7.

Example 1:

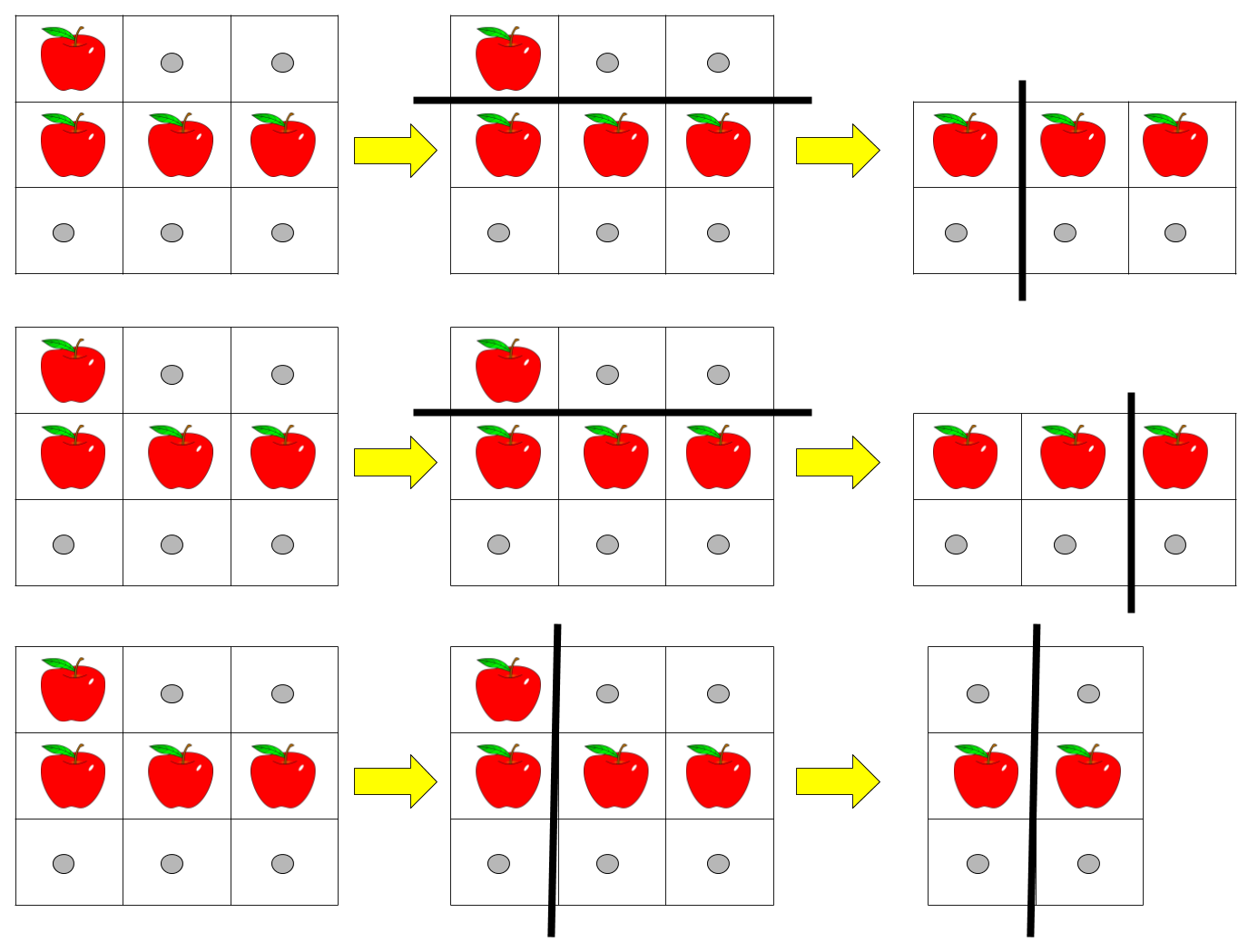
Input: pizza = ["A..","AAA","..."], k = 3
Output: 3 
Explanation: The figure above shows the three ways to cut the pizza. Note that pieces must contain at least one apple.

Example 2:

Input: pizza = ["A..","AA.","..."], k = 3
Output: 1

Example 3:

Input: pizza = ["A..","A..","..."], k = 1
Output: 1

Constraints:

1 <= rows, cols <= 50
rows == pizza.length
cols == pizza[i].length
1 <= k <= 10
pizza consists of characters 'A' and '.' only.

中文题目

给你一个 rows x cols 大小的矩形披萨和一个整数 k ，矩形包含两种字符： 'A' （表示苹果）和 '.' （表示空白格子）。你需要切披萨 k-1 次，得到 k 块披萨并送给别人。

切披萨的每一刀，先要选择是向垂直还是水平方向切，再在矩形的边界上选一个切的位置，将披萨一分为二。如果垂直地切披萨，那么需要把左边的部分送给一个人，如果水平地切，那么需要把上面的部分送给一个人。在切完最后一刀后，需要把剩下来的一块送给最后一个人。

请你返回确保每一块披萨包含至少一个苹果的切披萨方案数。由于答案可能是个很大的数字，请你返回它对 10^9 + 7 取余的结果。

示例 1：

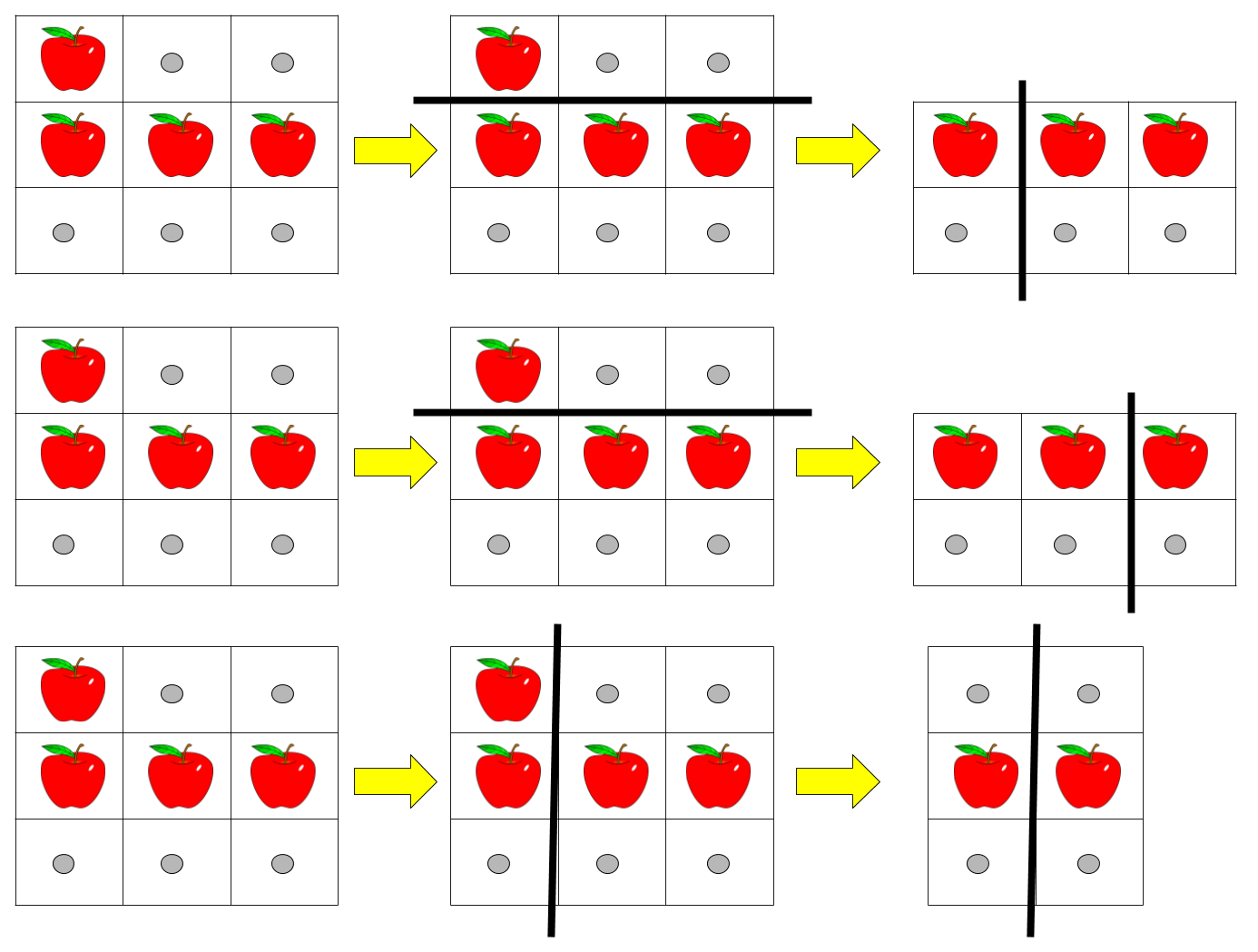
输入：pizza = ["A..","AAA","..."], k = 3
输出：3 
解释：上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。

示例 2：

输入：pizza = ["A..","AA.","..."], k = 3
输出：1

示例 3：

输入：pizza = ["A..","A..","..."], k = 1
输出：1

提示：

1 <= rows, cols <= 50
rows == pizza.length
cols == pizza[i].length
1 <= k <= 10
pizza 只包含字符 'A' 和 '.' 。

通过代码

高赞题解

题意

本题是统计切割方案数，一看就是使用dp，怎么来思考呢？
首先我们考虑存在的状态数：
毫无疑问，披萨被切成k块肯定是状态之一。
而如何表示当前剩余部分的披萨呢？题中说把左边和上边给一个人，可以知道，右下部分总是会剩余下来。
所以可以记录左上角的位置来表示剩余的披萨。

因此一个三维数组可以做为dp数组：dp[i][j][k]
i,j表示披萨剩余部分的左上角,k表示当前披萨被切成k块
初始状态显而易见，由于只有一块，没有切，左上角为(0,0)，所以dp[0][0][1]=1

状态转移

知道初始状态后，我们就要开始进行状态转移了~
首先让我们来考虑怎么从一块变成两块

披萨：
A..
AAA
...

由于我们知道可以水平切和垂直切，左上角为(i,j)，一刀切下去，可以从k变成k+1
因此，我们可以穷举每个状态水平切和垂直切的所有切法，来得到k+1的状态。
因为每切一次得到的剩余披萨左上角都不同，所以不会出现重复。
首先水平切：

左上角为(0,0),k=1
A..                                 A..
+++                                 AAA  
AAA                                 +++
...                                 ...
剩余部分：左上角为(1,0),k=2           剩余部分：左上角为(2,0),k=2 (不合理)

有这两种切法，很清楚看出来，第二种切法是不可以的，因为下面那一部分不存在A，不符合题意。
如何判断剩余和切出来的披萨存不存在A，我们先记下这个问题，后面会提到。
所以可以得到水平切的状态转移方程：

记原来的左上角为(i,j),新的左上角为(x,y)
if(两部分都存在A){
dp[x][y][k+1]+=dp[i][j][k]
}

有人说看不懂状态转移方程，所以就再稍微解释一下：
假设现在披萨的左上角为(i,j)而且已经被切成k块。
现在想再切一刀，不管是水平切还是垂直切，都要把披萨切成两块，而且我们要保证两块披萨都有A(都需要有A是显而易见的)
假如有一块不存在A，是不是不合理，就不用转移了，这就是加上条件的原因。

在两块都有A之后为什么这么转移呢？
水平切我们会保留下边的披萨，垂直切我们会保留右边的披萨，这就代表切开之后，新披萨的左上角是不是固定的？
我们把这个左上角记为(x,y)而且显然已经被切成k+1块
这是不是表示我们可以从状态dp[i][j][k]转移为dp[x][y][k+1]?

明白了这些，再来说为什么要使用dp[x][y][k+1]+=dp[i][j][k];

状态:左上角为(x,y)而且被切成k+1块是不是可能从多个状态转移过来？
比如说从dp[i1][j1][k],dp[i2][j2][k],……,dp[in][jn][k]都可以转移到dp[x][y][k+1]
每个状态转移到dp[x][y][k+1]只能切一刀(即每个状态转移到新状态的切法唯一)
是不是就说明dp[x][y][k+1]新增切法数是不是就是dp[i][j][k]
所以dp[x][y][k+1]+=dp[i][j][k]

垂直切是和水平切一样的，就不说了。

解决存在A的问题

我们如何判断切开后的两块披萨是否存在A呢？
方法1：直接暴力求解，我不知道会不会超时，我没有试，有兴趣可以写一下。
方法2：利用数学知识，计算出来对应披萨块中A的数量，假如数量大于0，则存在A
方法3：别的方法，假如有人愿意分享更简单的，可以在评论分享，大家一起进步

我使用方法2，所以就写一下方法2：
用数组num[i][j]表示以(0,0)为左上角，(i,j)为右下角的披萨块中包含的A数量，就是前缀和

上例中：
num:
1 1 1
2 3 4
2 3 4

怎么计算num数组使用简单的dp和数学知识就可以了，这里就不再赘述。
通过num数组和获得披萨块的左上角和右下角就可以轻易地算出A的个数：

这个大家肯定都会，就举个例子吧，就是简单的数学关系：
例：计算以(1,0)为左上角，(2,2)为右下角的披萨块A数目：
num[2][2]-num[0][2]-num[2][-1]+num[0][-1];
c++中没有负数下标，所以应该不存在这个前缀和，为了不影响结果，下标中出现-1的num值都用0代替：
所以为4-1-0-0=3

看不懂的可以直接看代码如何计算A数目，一看就明白了

大体步骤：

1.计算num
2.初始化dp[0][0][1]=1
3.状态转移填充
4.计算答案

代码

#define ll long long int

class Solution {
public:

    const ll mod=1e9+7;
    int ways(vector<string>& pizza, int k) {
        int row=pizza.size(),col=pizza[0].length();
        //计算num
        vector<vector<int>> num(row,vector<int>(col,0));
        if(pizza[0][0]=='A') num[0][0]=1;
        for(int i=1;i<row;i++) num[i][0]=num[i-1][0]+(pizza[i][0]=='A');
        for(int i=1;i<col;i++) num[0][i]=num[0][i-1]+(pizza[0][i]=='A');
        for(int i=1;i<row;i++) for(int j=1;j<col;j++)
                num[i][j]=num[i-1][j]+num[i][j-1]-num[i-1][j-1]+(pizza[i][j]=='A');
            
        //初始化dp
        vector<vector<vector<ll>>> dp(row,vector<vector<ll>>(col,vector<ll>(k+1,0)));
        dp[0][0][1]=1;

        //从k=2开始填充
        for(int x=2;x<=k;x++){
            for(int i=0;i<row;i++){
                for(int j=0;j<col;j++){
                    //dp为0代表不存在这种情况
                    if(dp[i][j][x-1]==0)
                        continue;
                    //穷举水平切
                    for(int z=i+1;z<row;z++){
                        if(hasA(num,i,j,z-1,col-1) && hasA(num,z,j,row-1,col-1)){
                            dp[z][j][x]+=dp[i][j][x-1];
                            dp[z][j][x]%=mod;
                        }
                    }
                    //穷举垂直切
                    for(int z=j+1;z<col;z++){
                        if(hasA(num,i,j,row-1,z-1) && hasA(num,i,z,row-1,col-1)){
                            dp[i][z][x]+=dp[i][j][x-1];
                           dp[i][z][x]%=mod;
                        }
                    }
                }
            }
        }
            
        //计算答案
        ll ans=0;
        for(int i=0;i<row;i++){
            for(int j=0;j<col;j++){
                ans+=dp[i][j][k];
            }
            ans%=mod;
        }
        return ans;
    }
        
    //计算存在A吗
    bool hasA(vector<vector<int>>& num,int sr,int sc,int er,int ec){
        int num1=0,num2=0,num3=0,res;
        if(sr!=0 && sc!=0) num1=num[sr-1][sc-1];
        if(sr!=0) num2=num[sr-1][ec];
        if(sc!=0) num3=num[er][sc-1];
        return num[er][ec]-num2-num3+num1>0;
    }
};

有不明白的同学可以继续在评论区交流，我看到就会回复的
谢谢，求赞

统计信息

通过次数	提交次数	AC比率
2717	5154	52.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途