原文链接: https://leetcode-cn.com/problems/maximum-number-of-darts-inside-of-a-circular-dartboard
英文原文
You have a very large square wall and a circular dartboard placed on the wall. You have been challenged to throw darts into the board blindfolded. Darts thrown at the wall are represented as an array of points on a 2D plane.
Return the maximum number of points that are within or lie on any circular dartboard of radius r.
Example 1:
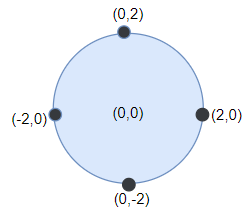
Input: points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2 Output: 4 Explanation: Circle dartboard with center in (0,0) and radius = 2 contain all points.
Example 2:
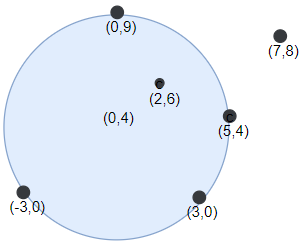
Input: points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5 Output: 5 Explanation: Circle dartboard with center in (0,4) and radius = 5 contain all points except the point (7,8).
Example 3:
Input: points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1 Output: 1
Example 4:
Input: points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2 Output: 4
Constraints:
1 <= points.length <= 100points[i].length == 2-10^4 <= points[i][0], points[i][1] <= 10^41 <= r <= 5000
中文题目
墙壁上挂着一个圆形的飞镖靶。现在请你蒙着眼睛向靶上投掷飞镖。
投掷到墙上的飞镖用二维平面上的点坐标数组表示。飞镖靶的半径为 r 。
请返回能够落在 任意 半径为 r 的圆形靶内或靶上的最大飞镖数。
示例 1:
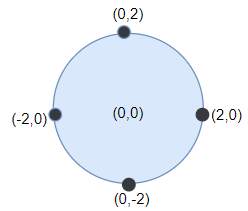
输入:points = [[-2,0],[2,0],[0,2],[0,-2]], r = 2 输出:4 解释:如果圆形的飞镖靶的圆心为 (0,0) ,半径为 2 ,所有的飞镖都落在靶上,此时落在靶上的飞镖数最大,值为 4 。
示例 2:
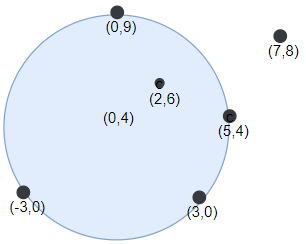
输入:points = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5 输出:5 解释:如果圆形的飞镖靶的圆心为 (0,4) ,半径为 5 ,则除了 (7,8) 之外的飞镖都落在靶上,此时落在靶上的飞镖数最大,值为 5 。
示例 3:
输入:points = [[-2,0],[2,0],[0,2],[0,-2]], r = 1 输出:1
示例 4:
输入:points = [[1,2],[3,5],[1,-1],[2,3],[4,1],[1,3]], r = 2 输出:4
提示:
1 <= points.length <= 100points[i].length == 2-10^4 <= points[i][0], points[i][1] <= 10^41 <= r <= 5000
通过代码
高赞题解
题意
本题就是要计算给定半径,圆心不定,然后算圆内的点数最多是多少
我们可以通过两点确定一个圆心,穷举所有的圆心即可。
计算圆心
先给一张图:
给定A(x1,y1) B(x2,y2) 以及圆心r
首先就可以直接计算出垂线长度h和mid坐标(AB中点)以及AB长度d:
d=sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
h=sqrt(r*r-(d/2.0)*(d/2.0))
mid=((x1+x2)/2.0,(y1+y2)/2.0)
然后我们的目的是求O(x,y)
我们使用向量。
看这个图:
向量a+向量b=向量c
毫无疑问
向量a就是mid坐标,向量b就是AB垂线的单位方向向量乘以高度h,向量c就是O坐标
所以现在唯一的问题就在于如何计算AB垂线的方向向量
向量AB=(x3,y3) 垂线的向量即为(-y3,x3)和(y3,-x3)
点积为0
特殊情况,AB长度大于2*r (d>2r) ,此时不存在圆心
还不明白的可以看一下代码,就会了:
代码
经@灵茶山艾府 指正,因为我穷举a b后还会穷举b a,所以每组只用计算一个圆心即可。
另一个方向的圆心会在第二次枚举的时候被计算出来。
struct point{
double x,y;
point(double i,double j):x(i),y(j){}
};
//算两点距离
double dist(double x1,double y1,double x2,double y2){
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
//计算圆心
point f(point& a,point& b,int r){
//算中点
point mid((a.x+b.x)/2.0,(a.y+b.y)/2.0);
//AB距离的一半
double d=dist(a.x,a.y,mid.x,mid.y);
//计算h
double h=sqrt(r*r-d*d);
//计算垂线
point ba(b.x-a.x,b.y-a.y);
point hd(-ba.y,ba.x);
double len=sqrt(hd.x*hd.x+hd.y*hd.y);
hd.x/=len,hd.y/=len;
hd.x*=h,hd.y*=h;
return point(hd.x+mid.x,hd.y+mid.y);
}
class Solution {
public:
int numPoints(vector<vector<int>>& points, int r) {
int n=points.size();
int ans=0;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(i==j){//一个点
int cnt=0;
for(int k=0;k<n;k++){
double tmp=dist(points[i][0],points[i][1],points[k][0],points[k][1]);
if(tmp<=r) cnt++;
}
ans=max(cnt,ans);
}else{//两个点
//通过长度判断有没有圆心
double d=dist(points[i][0],points[i][1],points[j][0],points[j][1]);
if(d/2>r) continue;
point a(points[i][0],points[i][1]),b(points[j][0],points[j][1]);
point res=f(a,b,r);
int cnt=0;
for(int k=0;k<n;k++){
double tmp=dist(res.x,res.y,points[k][0],points[k][1]);
if(tmp<=r) cnt++;
}
ans=max(cnt,ans);
}
}
}
return ans;
}
};总结
计算圆心也是有别的方法的,在此仅分享这一种
求个赞
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 1695 | 4596 | 36.9% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




