英文原文
Given a rows x cols matrix grid representing a field of cherries. Each cell in grid represents the number of cherries that you can collect.
You have two robots that can collect cherries for you, Robot #1 is located at the top-left corner (0,0) , and Robot #2 is located at the top-right corner (0, cols-1) of the grid.
Return the maximum number of cherries collection using both robots by following the rules below:
- From a cell (i,j), robots can move to cell (i+1, j-1) , (i+1, j) or (i+1, j+1).
- When any robot is passing through a cell, It picks it up all cherries, and the cell becomes an empty cell (0).
- When both robots stay on the same cell, only one of them takes the cherries.
- Both robots cannot move outside of the grid at any moment.
- Both robots should reach the bottom row in the
grid.
Example 1:
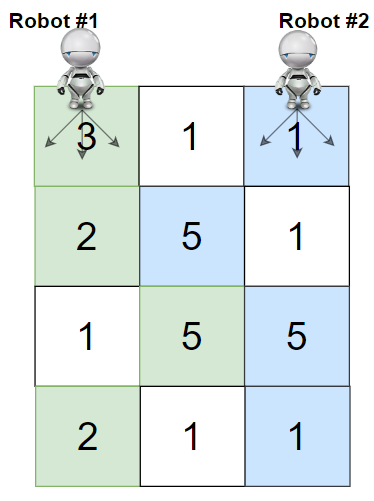
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]] Output: 24 Explanation: Path of robot #1 and #2 are described in color green and blue respectively. Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12. Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12. Total of cherries: 12 + 12 = 24.
Example 2:
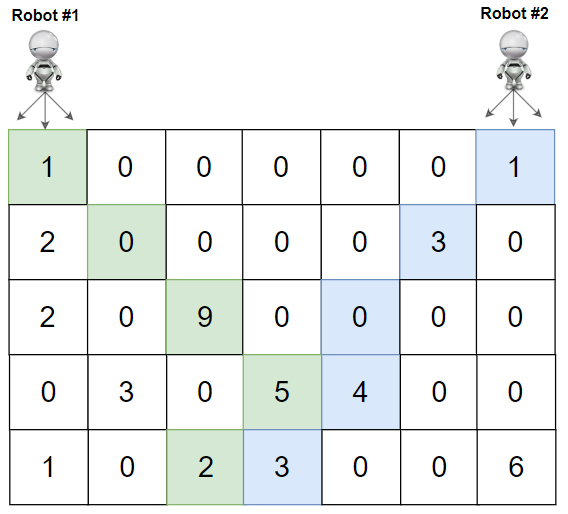
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]] Output: 28 Explanation: Path of robot #1 and #2 are described in color green and blue respectively. Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17. Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11. Total of cherries: 17 + 11 = 28.
Example 3:
Input: grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]] Output: 22
Example 4:
Input: grid = [[1,1],[1,1]] Output: 4
Constraints:
rows == grid.lengthcols == grid[i].length2 <= rows, cols <= 700 <= grid[i][j] <= 100
中文题目
给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。
你有两个机器人帮你收集樱桃,机器人 1 从左上角格子 (0,0) 出发,机器人 2 从右上角格子 (0, cols-1) 出发。
请你按照如下规则,返回两个机器人能收集的最多樱桃数目:
- 从格子
(i,j)出发,机器人可以移动到格子(i+1, j-1),(i+1, j)或者(i+1, j+1)。 - 当一个机器人经过某个格子时,它会把该格子内所有的樱桃都摘走,然后这个位置会变成空格子,即没有樱桃的格子。
- 当两个机器人同时到达同一个格子时,它们中只有一个可以摘到樱桃。
- 两个机器人在任意时刻都不能移动到
grid外面。 - 两个机器人最后都要到达
grid最底下一行。
示例 1:
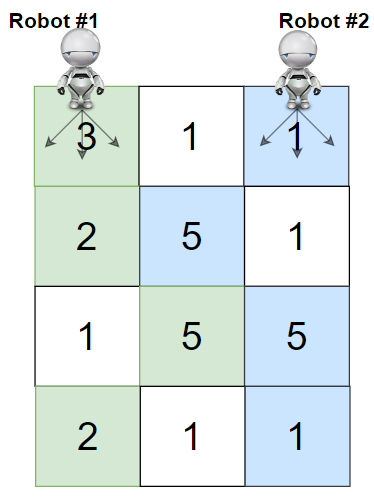
输入:grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]] 输出:24 解释:机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。 机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。 机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。 樱桃总数为: 12 + 12 = 24 。
示例 2:
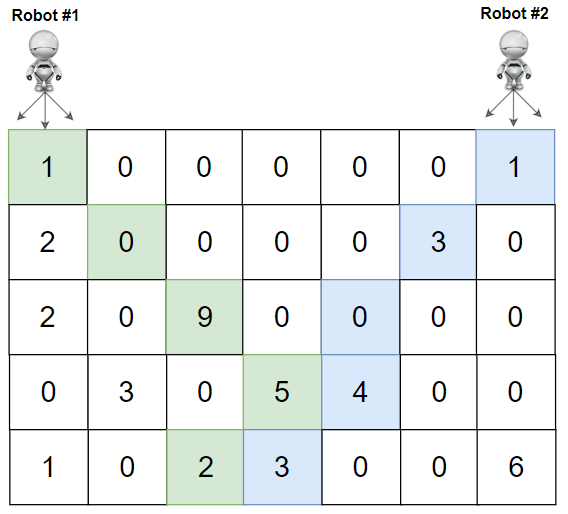
输入:grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]] 输出:28 解释:机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。 机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。 机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。 樱桃总数为: 17 + 11 = 28 。
示例 3:
输入:grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]] 输出:22
示例 4:
输入:grid = [[1,1],[1,1]] 输出:4
提示:
rows == grid.lengthcols == grid[i].length2 <= rows, cols <= 700 <= grid[i][j] <= 100
通过代码
高赞题解
思路
- 因为机器人都是按照行一步一步走下来的,所以按照行 dp
- 除了行号,还需要保存两个机器人的列号
- 如:
dp[1][2][3]就表示第 1 行,当机器人站在 2 和 3 列时摘的樱桃数量 - 然后从这个状态,走到下一行的最多 3 * 3 种可能进行转移,就是当前值,加上下一行机器人站的位置的樱桃数
- 走到最后,统计最大值即可
答题
[]int cherryPickup(vector<vector<int>>& grid) { if (grid.empty()) return 0; if (grid[0].empty()) return 0; vector<vector<vector<int>>> dp(grid.size(), vector<vector<int>>(grid[0].size(), vector<int>(grid[0].size(), 0))); dp[0][0][grid[0].size() - 1] = grid[0][0] + grid[0].back() + 1; int ans = 0; for (int i = 0; i < grid.size() - 1; i++) { for (int a = 0; a < grid[0].size(); a++) { for (int b = a; b < grid[0].size(); b++) { if (dp[i][a][b] == 0) continue; for (int ar = max(a - 1, 0); ar < min(a + 2, (int)grid[0].size()); ar++) { for (int br = max(b - 1, 0); br < min(b + 2, (int)grid[0].size()); br++) { int art = (ar < br) ? ar : br; int brt = (ar < br) ? br : ar; int newVal = dp[i][a][b] + grid[i + 1][art] + grid[i + 1][brt]; newVal -= (art == brt) ? grid[i + 1][art] : 0; dp[i + 1][art][brt] = max(dp[i + 1][art][brt], newVal); } } } } } for (int a = 0; a < grid[0].size(); a++) { for (int b = a; b < grid[0].size(); b++) { ans = max(ans, dp.back()[a][b]); } } return ans - 1; }
致谢
感谢您的观看,希望对您有帮助,欢迎热烈的交流!
如果感觉还不错就点个赞吧~
这是 我的leetcode ,帮助我收集整理题目,可以方便的 visual studio 调试,欢迎关注,star
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 2771 | 4664 | 59.4% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




