原文链接: https://leetcode-cn.com/problems/allocate-mailboxes

英文原文

Given the array houses and an integer k. where houses[i] is the location of the ith house along a street, your task is to allocate k mailboxes in the street.

Return the minimum total distance between each house and its nearest mailbox.

The answer is guaranteed to fit in a 32-bit signed integer.

 

Example 1:

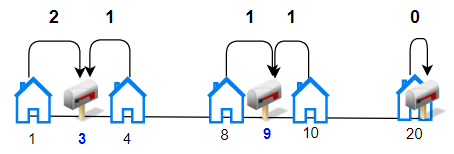
Input: houses = [1,4,8,10,20], k = 3
Output: 5
Explanation: Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 

Example 2:

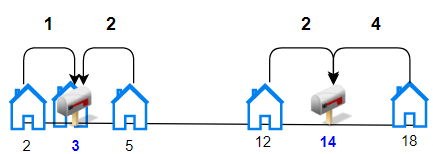
Input: houses = [2,3,5,12,18], k = 2
Output: 9
Explanation: Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.

Example 3:

Input: houses = [7,4,6,1], k = 1
Output: 8

Example 4:

Input: houses = [3,6,14,10], k = 4
Output: 0

 

Constraints:

• n == houses.length
• 1 <= n <= 100
• 1 <= houses[i] <= 10^4
• 1 <= k <= n
• Array houses contain unique integers.

中文题目

给你一个房屋数组houses 和一个整数 k ，其中 houses[i] 是第 i 栋房子在一条街上的位置，现需要在这条街上安排 k 个邮筒。

请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。

答案保证在 32 位有符号整数范围以内。

 

示例 1：

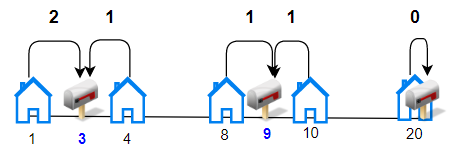
输入：houses = [1,4,8,10,20], k = 3
输出：5
解释：将邮筒分别安放在位置 3， 9 和 20 处。
每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。

示例 2：

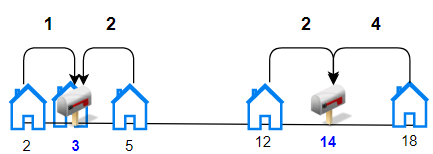
输入：houses = [2,3,5,12,18], k = 2
输出：9
解释：将邮筒分别安放在位置 3 和 14 处。
每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。

示例 3：

输入：houses = [7,4,6,1], k = 1
输出：8

示例 4：

输入：houses = [3,6,14,10], k = 4
输出：0

 

提示：

• n == houses.length
• 1 <= n <= 100
• 1 <= houses[i] <= 10^4
• 1 <= k <= n
• 数组 houses 中的整数互不相同。

通过代码

高赞题解

解题思路

动态规划。给定一个数组，如果安排一个邮局的话，那么将这个邮箱放到这个数组的中位数的位置上，所有的距离之和是最小的。(绝对值不等式)

当给了K个邮局的话，可以使用动态规划来求解。

按照最后一个邮箱的覆盖范围来划分。dp[i][j] 表示i个数，j个邮局，的最小划分方法。

那么枚举最后一个邮箱负责的范围，最大的范围是，前j - 1 个邮箱各自负责一个房子，那么最后一个就负责了j - 1到i的所有房子
最小的范围就是只负责第i个房子。

所以有dp[i][j] = min(dp[k - 1][j - 1] + rec[k][i], dp[i][j]) 对于k >= j - 1 && k <= i

rec[i][j] 表示从第i个房子到第j个房子，用一个邮箱最小的花费。可以提前预处理好所有的情况。

个人博客

感谢赫连昊栋奆佬的提示QAQ，奆佬博客地址

PS:
有人想到用层次聚类做么(逃

代码

class Solution {
public:
    int minDistance(vector<int>& houses, int K) {
        sort(houses.begin(), houses.end());
        int n = houses.size();
        vector<vector<int>> rec(n, vector<int>(n, 0));
        for(int i = 0; i < n; i ++){
            for(int j = i; j < n; j ++){
                int mid = i + j >> 1;
                for(int k = i; k <= j; k ++){
                    rec[i][j] += abs(houses[k] - houses[mid]);
                }
            }
        }
        vector<vector<int>> dp(n, vector<int>(K + 1, 2e9));
        for(int i = 0; i < n; i ++) dp[i][1] = rec[0][i];
        for(int i = 0; i < n; i ++){
            for(int j = 2; j <= min(i + 1, K); j ++){
                for(int k = j - 1; k <= i; k ++){
                    dp[i][j] = min(dp[i][j], dp[k - 1][j - 1] + rec[k][i]);
                }
            }
        }
        return dp[n-1][K];
    }
};

统计信息

通过次数	提交次数	AC比率
2829	4861	58.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言