原文链接: https://leetcode-cn.com/problems/kth-ancestor-of-a-tree-node

英文原文

You are given a tree with n nodes numbered from 0 to n - 1 in the form of a parent array parent where parent[i] is the parent of ith node. The root of the tree is node 0. Find the kth ancestor of a given node.

The kth ancestor of a tree node is the kth node in the path from that node to the root node.

Implement the TreeAncestor class:

• TreeAncestor(int n, int[] parent) Initializes the object with the number of nodes in the tree and the parent array.
• int getKthAncestor(int node, int k) return the kth ancestor of the given node node. If there is no such ancestor, return -1.

 

Example 1:

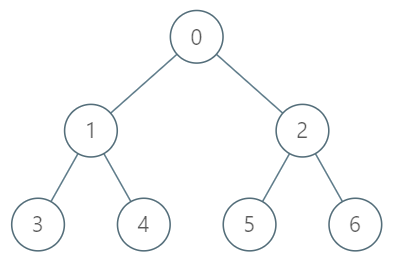
Input
["TreeAncestor", "getKthAncestor", "getKthAncestor", "getKthAncestor"]
[[7, [-1, 0, 0, 1, 1, 2, 2]], [3, 1], [5, 2], [6, 3]]
Output
[null, 1, 0, -1]

Explanation
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor

 

Constraints:

• 1 <= k <= n <= 5 * 104
• parent.length == n
• parent[0] == -1
• 0 <= parent[i] < n for all 0 < i < n
• 0 <= node < n
• There will be at most 5 * 104 queries.

中文题目

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

请你设计并实现 getKthAncestor(int node, int k) 函数，函数返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

 

示例：

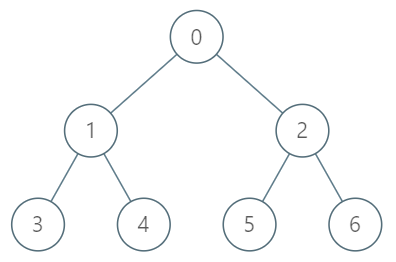
输入：
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]

输出：
[null,1,0,-1]

解释：
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);

treeAncestor.getKthAncestor(3, 1);  // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2);  // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3);  // 返回 -1 因为不存在满足要求的祖先节点

 

提示：

• 1 <= k <= n <= 5*10^4
• parent[0] == -1 表示编号为 0 的节点是根节点。
• 对于所有的 0 < i < n ，0 <= parent[i] < n 总成立
• 0 <= node < n
• 至多查询 5*10^4 次

通过代码

高赞题解

因为力扣的数据还是有些弱的，所以这个问题我看到一些相对“暴力”的解也能过。但是这个问题的“正规解”应该是 Binary Lifting。

Binary Lifting 的本质其实是 dp。dp[node][j] 存储的是 node 节点距离为 2^j 的祖先是谁。

根据定义，dp[node][0] 就是 parent[node]，即 node 的距离为 1 的祖先是 parent[node]。

状态转移是： dp[node][j] = dp[dp[node][j - 1]][j - 1]。

意思是：要想找到 node 的距离 2^j 的祖先，先找到 node 的距离 2^(j - 1) 的祖先，然后，再找这个祖先的距离 2^(j - 1) 的祖先。两步得到 node 的距离为 2^j 的祖先。

所以，我们要找到每一个 node 的距离为 1, 2, 4, 8, 16, 32, … 的祖先，直到达到树的最大的高度。树的最大的高度是 logn 级别的。

这样做，状态总数是 O(nlogn)，可以使用 O(nlogn) 的时间做预处理。

之后，根据预处理的结果，可以在 O(logn) 的时间里完成每次查询：对于每一个查询 k，把 k 拆解成二进制表示，然后根据二进制表示中 1 的位置，累计向上查询。

我的参考代码（C++）：

class TreeAncestor {

private:
    vector<vector<int>> dp;

public:
    TreeAncestor(int n, vector<int>& parent) : dp(n) {

        for(int i = 0; i < n; i ++)
            dp[i].push_back(parent[i]);

        for(int j = 1; ; j ++){
            bool allneg = true;
            for(int i = 0; i < n; i ++){
                int t = dp[i][j - 1] != -1 ? dp[dp[i][j - 1]][j - 1] : -1;
                dp[i].push_back(t);
                if(t != -1) allneg = false;
            }
            if(allneg) break; // 所有的节点的 2^j 的祖先都是 -1 了，就不用再计算了
        }
    }

    int getKthAncestor(int node, int k) {

        if(k == 0 || node== -1) return node;

        int pos = ffs(k) - 1; // C++ 语言中 ffs(k) 求解出 k 的最右侧第一个 1 的位置（1-based）

        return pos < dp[node].size() ? getKthAncestor(dp[node][pos], k - (1 << pos)) : -1;
    }
};

上面的 query 使用递归写法，再提供一个非递归写法，可能对有些同学来说更清晰：

int getKthAncestor(int node, int k) {

    int res = node, pos = 0;
    while(k && res != -1){
        if(pos >= dp[res].size()) return -1;
        if(k & 1) res = dp[res][pos];
        k >>= 1, pos ++;
    }
    return res;
}

---

觉得有帮助请点赞哇！

统计信息

通过次数	提交次数	AC比率
3458	11487	30.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言