原文链接: https://leetcode-cn.com/problems/find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree

英文原文

Given a weighted undirected connected graph with n vertices numbered from 0 to n - 1, and an array edges where edges[i] = [ai, bi, weighti] represents a bidirectional and weighted edge between nodes ai and bi. A minimum spanning tree (MST) is a subset of the graph's edges that connects all vertices without cycles and with the minimum possible total edge weight.

Find all the critical and pseudo-critical edges in the given graph's minimum spanning tree (MST). An MST edge whose deletion from the graph would cause the MST weight to increase is called a critical edge. On the other hand, a pseudo-critical edge is that which can appear in some MSTs but not all.

Note that you can return the indices of the edges in any order.

 

Example 1:

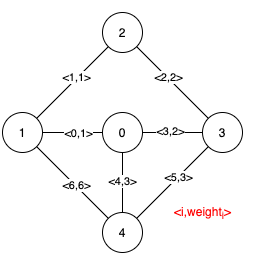
Input: n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
Output: [[0,1],[2,3,4,5]]
Explanation: The figure above describes the graph.
The following figure shows all the possible MSTs:

Notice that the two edges 0 and 1 appear in all MSTs, therefore they are critical edges, so we return them in the first list of the output.
The edges 2, 3, 4, and 5 are only part of some MSTs, therefore they are considered pseudo-critical edges. We add them to the second list of the output.

Example 2:

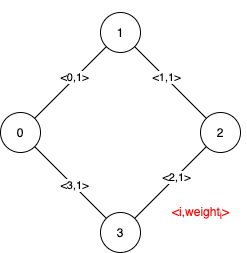
Input: n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
Output: [[],[0,1,2,3]]
Explanation: We can observe that since all 4 edges have equal weight, choosing any 3 edges from the given 4 will yield an MST. Therefore all 4 edges are pseudo-critical.

 

Constraints:

• 2 <= n <= 100
• 1 <= edges.length <= min(200, n * (n - 1) / 2)
• edges[i].length == 3
• 0 <= ai < bi < n
• 1 <= weighti <= 1000
• All pairs (ai, bi) are distinct.

中文题目

给你一个 n 个点的带权无向连通图，节点编号为 0 到 n-1 ，同时还有一个数组 edges ，其中 edges[i] = [fromi, toi, weighti] 表示在 fromi 和 toi 节点之间有一条带权无向边。最小生成树 (MST) 是给定图中边的一个子集，它连接了所有节点且没有环，而且这些边的权值和最小。

请你找到给定图中最小生成树的所有关键边和伪关键边。如果从图中删去某条边，会导致最小生成树的权值和增加，那么我们就说它是一条关键边。伪关键边则是可能会出现在某些最小生成树中但不会出现在所有最小生成树中的边。

请注意，你可以分别以任意顺序返回关键边的下标和伪关键边的下标。

 

示例 1：

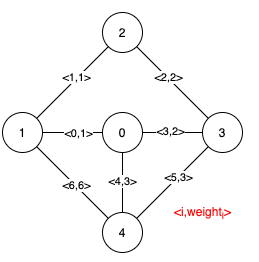
输入：n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
输出：[[0,1],[2,3,4,5]]
解释：上图描述了给定图。
下图是所有的最小生成树。

注意到第 0 条边和第 1 条边出现在了所有最小生成树中，所以它们是关键边，我们将这两个下标作为输出的第一个列表。
边 2，3，4 和 5 是所有 MST 的剩余边，所以它们是伪关键边。我们将它们作为输出的第二个列表。

示例 2 ：

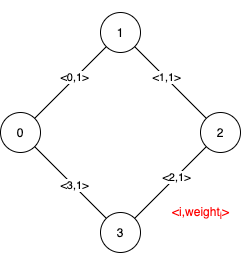
输入：n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
输出：[[],[0,1,2,3]]
解释：可以观察到 4 条边都有相同的权值，任选它们中的 3 条可以形成一棵 MST 。所以 4 条边都是伪关键边。

 

提示：

• 2 <= n <= 100
• 1 <= edges.length <= min(200, n * (n - 1) / 2)
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti <= 1000
• 所有 (fromi, toi) 数对都是互不相同的。

通过代码

高赞题解

前言

要想解决本题，需要用到「最小生成树」以及对应求解最小生成树的「$\texttt{Kruskal}$ 算法」。

对上述算法和数据结构的讲解不是本篇题解的重点，因此这里希望读者在对掌握了这些知识点之后，再来尝试解决本题。

本篇题解中会给出两种算法，并且每种算法都默认读者已经掌握了对应的知识点：

• 方法一只需要枚举每一条边，并用略微修改的 $\texttt{Kruskal}$ 算法判断其是否是关键边或伪关键边；

• 方法二利用了 $\texttt{Kruskal}$ 算法的连通性性质，以及无向图找桥边的 $\texttt{Tarjan}$ 算法，即使在竞赛中也不算容易，仅供读者挑战自我。

方法一：枚举 + 最小生成树判定

思路与算法

我们首先需要理解题目描述中对于「关键边」和「伪关键边」的定义：

• 关键边：如果最小生成树中删去某条边，会导致最小生成树的权值和增加，那么我们就说它是一条关键边。也就是说，如果设原图最小生成树的权值为 $\textit{value}$，那么去掉这条边后：

  • 要么整个图不连通，不存在最小生成树；

  • 要么整个图联通，对应的最小生成树的权值为 $v$，其严格大于 $\textit{value}$。

• 伪关键边：可能会出现在某些最小生成树中但不会出现在所有最小生成树中的边。也就是说，我们可以在计算最小生成树的过程中，最先考虑这条边，即最先将这条边的两个端点在并查集中合并。设最终得到的最小生成树权值为 $v$，如果 $v = \textit{value}$，那么这条边就是伪关键边。

需要注意的是，关键边也满足伪关键边对应的性质。因此，我们首先对原图执行 $\texttt{Kruskal}$ 算法，得到最小生成树的权值 $\textit{value}$，随后我们枚举每一条边，首先根据上面的方法判断其是否是关键边，如果不是关键边，再判断其是否是伪关键边。

代码

[sol1-C++]
// 并查集模板
class UnionFind {
public:
    vector<int> parent;
    vector<int> size;
    int n;
    // 当前连通分量数目
    int setCount;
    
public:
    UnionFind(int _n): n(_n), setCount(_n), parent(_n), size(_n, 1) {
        iota(parent.begin(), parent.end(), 0);
    }
    
    int findset(int x) {
        return parent[x] == x ? x : parent[x] = findset(parent[x]);
    }
    
    bool unite(int x, int y) {
        x = findset(x);
        y = findset(y);
        if (x == y) {
            return false;
        }
        if (size[x] < size[y]) {
            swap(x, y);
        }
        parent[y] = x;
        size[x] += size[y];
        --setCount;
        return true;
    }
    
    bool connected(int x, int y) {
        x = findset(x);
        y = findset(y);
        return x == y;
    }
};

class Solution {
public:
    vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges) {
        int m = edges.size();
        for (int i = 0; i < m; ++i) {
            edges[i].push_back(i);
        }
        sort(edges.begin(), edges.end(), [](const auto& u, const auto& v) {
            return u[2] < v[2];
        });

        // 计算 value
        UnionFind uf_std(n);
        int value = 0;
        for (int i = 0; i < m; ++i) {
            if (uf_std.unite(edges[i][0], edges[i][1])) {
                value += edges[i][2];
            }
        }

        vector<vector<int>> ans(2);
        
        for (int i = 0; i < m; ++i) {
            // 判断是否是关键边
            UnionFind uf(n);
            int v = 0;
            for (int j = 0; j < m; ++j) {
                if (i != j && uf.unite(edges[j][0], edges[j][1])) {
                    v += edges[j][2];
                }
            }
            if (uf.setCount != 1 || (uf.setCount == 1 && v > value)) {
                ans[0].push_back(edges[i][3]);
                continue;
            }

            // 判断是否是伪关键边
            uf = UnionFind(n);
            uf.unite(edges[i][0], edges[i][1]);
            v = edges[i][2];
            for (int j = 0; j < m; ++j) {
                if (i != j && uf.unite(edges[j][0], edges[j][1])) {
                    v += edges[j][2];
                }
            }
            if (v == value) {
                ans[1].push_back(edges[i][3]);
            }
        }
      
        return ans;
    }
};

[sol1-Java]
class Solution {
    public List<List<Integer>> findCriticalAndPseudoCriticalEdges(int n, int[][] edges) {
        int m = edges.length;
        int[][] newEdges = new int[m][4];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < 3; ++j) {
                newEdges[i][j] = edges[i][j];
            }
            newEdges[i][3] = i;
        }
        Arrays.sort(newEdges, new Comparator<int[]>() {
            public int compare(int[] u, int[] v) {
                return u[2] - v[2];
            }
        });

        // 计算 value
        UnionFind ufStd = new UnionFind(n);
        int value = 0;
        for (int i = 0; i < m; ++i) {
            if (ufStd.unite(newEdges[i][0], newEdges[i][1])) {
                value += newEdges[i][2];
            }
        }

        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        for (int i = 0; i < 2; ++i) {
            ans.add(new ArrayList<Integer>());
        }
        
        for (int i = 0; i < m; ++i) {
            // 判断是否是关键边
            UnionFind uf = new UnionFind(n);
            int v = 0;
            for (int j = 0; j < m; ++j) {
                if (i != j && uf.unite(newEdges[j][0], newEdges[j][1])) {
                    v += newEdges[j][2];
                }
            }
            if (uf.setCount != 1 || (uf.setCount == 1 && v > value)) {
                ans.get(0).add(newEdges[i][3]);
                continue;
            }

            // 判断是否是伪关键边
            uf = new UnionFind(n);
            uf.unite(newEdges[i][0], newEdges[i][1]);
            v = newEdges[i][2];
            for (int j = 0; j < m; ++j) {
                if (i != j && uf.unite(newEdges[j][0], newEdges[j][1])) {
                    v += newEdges[j][2];
                }
            }
            if (v == value) {
                ans.get(1).add(newEdges[i][3]);
            }
        }
      
        return ans;
    }
}

// 并查集模板
class UnionFind {
    int[] parent;
    int[] size;
    int n;
    // 当前连通分量数目
    int setCount;

    public UnionFind(int n) {
        this.n = n;
        this.setCount = n;
        this.parent = new int[n];
        this.size = new int[n];
        Arrays.fill(size, 1);
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }
    
    public int findset(int x) {
        return parent[x] == x ? x : (parent[x] = findset(parent[x]));
    }
    
    public boolean unite(int x, int y) {
        x = findset(x);
        y = findset(y);
        if (x == y) {
            return false;
        }
        if (size[x] < size[y]) {
            int temp = x;
            x = y;
            y = temp;
        }
        parent[y] = x;
        size[x] += size[y];
        --setCount;
        return true;
    }
    
    public boolean connected(int x, int y) {
        x = findset(x);
        y = findset(y);
        return x == y;
    }
}

[sol1-Python3]
# 并查集模板
class UnionFind:
    def __init__(self, n: int):
        self.parent = list(range(n))
        self.size = [1] * n
        self.n = n
        # 当前连通分量数目
        self.setCount = n
    
    def findset(self, x: int) -> int:
        if self.parent[x] == x:
            return x
        self.parent[x] = self.findset(self.parent[x])
        return self.parent[x]
    
    def unite(self, x: int, y: int) -> bool:
        x, y = self.findset(x), self.findset(y)
        if x == y:
            return False
        if self.size[x] < self.size[y]:
            x, y = y, x
        self.parent[y] = x
        self.size[x] += self.size[y]
        self.setCount -= 1
        return True
    
    def connected(self, x: int, y: int) -> bool:
        x, y = self.findset(x), self.findset(y)
        return x == y

class Solution:
    def findCriticalAndPseudoCriticalEdges(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        m = len(edges)
        for i, edge in enumerate(edges):
            edge.append(i)
        edges.sort(key=lambda x: x[2])

        # 计算 value
        uf_std = UnionFind(n)
        value = 0
        for i in range(m):
            if uf_std.unite(edges[i][0], edges[i][1]):
                value += edges[i][2]

        ans = [list(), list()]
        
        for i in range(m):
            # 判断是否是关键边
            uf = UnionFind(n)
            v = 0
            for j in range(m):
                if i != j and uf.unite(edges[j][0], edges[j][1]):
                    v += edges[j][2]
            if uf.setCount != 1 or (uf.setCount == 1 and v > value):
                ans[0].append(edges[i][3])
                continue

            # 判断是否是伪关键边
            uf = UnionFind(n)
            uf.unite(edges[i][0], edges[i][1])
            v = edges[i][2]
            for j in range(m):
                if i != j and uf.unite(edges[j][0], edges[j][1]):
                    v += edges[j][2]
            if v == value:
                ans[1].append(edges[i][3])
      
        return ans

[sol1-Golang]
type unionFind struct {
    parent, size []int
    setCount     int // 当前连通分量数目
}

func newUnionFind(n int) *unionFind {
    parent := make([]int, n)
    size := make([]int, n)
    for i := range parent {
        parent[i] = i
        size[i] = 1
    }
    return &unionFind{parent, size, n}
}

func (uf *unionFind) find(x int) int {
    if uf.parent[x] != x {
        uf.parent[x] = uf.find(uf.parent[x])
    }
    return uf.parent[x]
}

func (uf *unionFind) union(x, y int) bool {
    fx, fy := uf.find(x), uf.find(y)
    if fx == fy {
        return false
    }
    if uf.size[fx] < uf.size[fy] {
        fx, fy = fy, fx
    }
    uf.size[fx] += uf.size[fy]
    uf.parent[fy] = fx
    uf.setCount--
    return true
}

func findCriticalAndPseudoCriticalEdges(n int, edges [][]int) [][]int {
    for i, e := range edges {
        edges[i] = append(e, i)
    }
    sort.Slice(edges, func(i, j int) bool { return edges[i][2] < edges[j][2] })

    calcMST := func(uf *unionFind, ignoreID int) (mstValue int) {
        for i, e := range edges {
            if i != ignoreID && uf.union(e[0], e[1]) {
                mstValue += e[2]
            }
        }
        if uf.setCount > 1 {
            return math.MaxInt64
        }
        return
    }

    mstValue := calcMST(newUnionFind(n), -1)

    var keyEdges, pseudokeyEdges []int
    for i, e := range edges {
        // 是否为关键边
        if calcMST(newUnionFind(n), i) > mstValue {
            keyEdges = append(keyEdges, e[3])
            continue
        }

        // 是否为伪关键边
        uf := newUnionFind(n)
        uf.union(e[0], e[1])
        if e[2]+calcMST(uf, i) == mstValue {
            pseudokeyEdges = append(pseudokeyEdges, e[3])
        }
    }

    return [][]int{keyEdges, pseudokeyEdges}
}

[sol1-JavaScript]
var findCriticalAndPseudoCriticalEdges = function(n, edges) {
    const m = edges.length;
    for (const [i, edge] of edges.entries()) {
        edge.push(i);
    }
    edges.sort((a, b) => a[2] - b[2]);

    // 计算 value
    const uf_std = new UnionFind(n);
    let value = 0;
    for (let i = 0; i < m; i++) {
        if (uf_std.unite(edges[i][0], edges[i][1])) {
            value += edges[i][2];
        }
    }

    const ans = [[], []];

    for (let i = 0; i < m; i++) {
        // 判断是否是关键边
        let uf = new UnionFind(n);
        let v = 0;
        for (let j = 0; j < m; j++) {
            if (i !== j && uf.unite(edges[j][0], edges[j][1])) {
                v += edges[j][2];
            }
        }
        if (uf.setCount !== 1 || (uf.setCount === 1 && v > value)) {
            ans[0].push(edges[i][3]);
            continue;
        }

        // 判断是否是伪关键边
        uf = new UnionFind(n);
        uf.unite(edges[i][0], edges[i][1]);
        v = edges[i][2];
        for (let j = 0; j < m; j++) {
            if (i !== j && uf.unite(edges[j][0], edges[j][1])) {
                v += edges[j][2];
            }
        }
        if (v === value) {
            ans[1].push(edges[i][3]);
        }
    }
    return ans;
};

// 并查集模板
class UnionFind {
    constructor (n) {
        this.parent = new Array(n).fill(0).map((element, index) => index);
        this.size = new Array(n).fill(1);
        // 当前连通分量数目
        this.setCount = n;
    }

    findset (x) {
        if (this.parent[x] === x) {
            return x;
        }
        this.parent[x] = this.findset(this.parent[x]);
        return this.parent[x];
    }

    unite (a, b) {
        let x = this.findset(a), y = this.findset(b);
        if (x === y) {
            return false;
        }
        if (this.size[x] < this.size[y]) {
            [x, y] = [y, x];
        }
        this.parent[y] = x;
        this.size[x] += this.size[y];
        this.setCount -= 1;
        return true;
    }

    connected (a, b) {
        const x = this.findset(a), y = this.findset(b);
        return x === y;
    }
}

[sol1-C]
void swap(int* a, int* b) {
    int tmp = *a;
    *a = *b, *b = tmp;
}

struct Edge {
    int x, y, w, id;
};

int cmp(const void* a, const void* b) {
    return ((struct Edge*)a)->w - ((struct Edge*)b)->w;
}

struct DisjointSetUnion {
    int *f, *size;
    int n, setCount;
};

void initDSU(struct DisjointSetUnion* obj, int n) {
    obj->f = malloc(sizeof(int) * n);
    obj->size = malloc(sizeof(int) * n);
    obj->n = n;
    obj->setCount = n;
    for (int i = 0; i < n; i++) {
        obj->f[i] = i;
        obj->size[i] = 1;
    }
}

void freeDSU(struct DisjointSetUnion* obj) {
    free(obj->f);
    free(obj->size);
    free(obj);
}

int find(struct DisjointSetUnion* obj, int x) {
    return obj->f[x] == x ? x : (obj->f[x] = find(obj, obj->f[x]));
}

int unionSet(struct DisjointSetUnion* obj, int x, int y) {
    int fx = find(obj, x), fy = find(obj, y);
    if (fx == fy) {
        return false;
    }
    if (obj->size[fx] < obj->size[fy]) {
        swap(&fx, &fy);
    }
    obj->size[fx] += obj->size[fy];
    obj->f[fy] = fx;
    obj->setCount--;
    return true;
}

int** findCriticalAndPseudoCriticalEdges(int n, int** edges, int edgesSize, int* edgesColSize, int* returnSize, int** returnColumnSizes) {
    int m = edgesSize;
    struct Edge edgesTmp[m];
    for (int i = 0; i < m; i++) {
        edgesTmp[i].x = edges[i][0];
        edgesTmp[i].y = edges[i][1];
        edgesTmp[i].w = edges[i][2];
        edgesTmp[i].id = i;
    }
    qsort(edgesTmp, m, sizeof(struct Edge), cmp);

    struct DisjointSetUnion* ufStd = malloc(sizeof(struct DisjointSetUnion));
    initDSU(ufStd, n);

    int value = 0;
    for (int i = 0; i < m; ++i) {
        if (unionSet(ufStd, edgesTmp[i].x, edgesTmp[i].y)) {
            value += edgesTmp[i].w;
        }
    }
    freeDSU(ufStd);

    *returnSize = 2;
    int** ans = malloc(sizeof(int*) * 2);
    for (int i = 0; i < 2; i++) {
        ans[i] = malloc(sizeof(int) * m);
    }
    *returnColumnSizes = malloc(sizeof(int) * 2);
    memset(*returnColumnSizes, 0, sizeof(int) * 2);

    for (int i = 0; i < m; ++i) {
        // 判断是否是关键边
        struct DisjointSetUnion* uf1 = malloc(sizeof(struct DisjointSetUnion));
        initDSU(uf1, n);

        int v = 0;
        for (int j = 0; j < m; ++j) {
            if (i != j && unionSet(uf1, edgesTmp[j].x, edgesTmp[j].y)) {
                v += edgesTmp[j].w;
            }
        }
        if (uf1->setCount != 1 || (uf1->setCount == 1 && v > value)) {
            ans[0][(*returnColumnSizes)[0]++] = edgesTmp[i].id;
            continue;
        }
        freeDSU(uf1);

        // 判断是否是伪关键边
        struct DisjointSetUnion* uf2 = malloc(sizeof(struct DisjointSetUnion));
        initDSU(uf2, n);
        unionSet(uf2, edgesTmp[i].x, edgesTmp[i].y);
        v = edgesTmp[i].w;
        for (int j = 0; j < m; ++j) {
            if (i != j && unionSet(uf2, edgesTmp[j].x, edgesTmp[j].y)) {
                v += edgesTmp[j].w;
            }
        }
        if (v == value) {
            ans[1][(*returnColumnSizes)[1]++] = edgesTmp[i].id;
        }
    }
    return ans;
}

复杂度分析

• 时间复杂度：$O(m^2 \cdot \alpha(n))$，其中 $n$ 和 $m$ 分别是图中的节点数和边数。我们首先需要对所有的边进行排序，时间复杂度为 $O(m \log m)$。一次 $\texttt{Kruskal}$ 算法的时间复杂度为 $O(m \cdot \alpha(n))$，其中 $\alpha$ 是阿克曼函数的反函数。我们最多需要执行 $2m + 1$ 次 $\texttt{Kruskal}$ 算法，时间复杂度为 $O(m^2 \alpha(n))$，在渐进意义下大于排序的时间复杂度，因此前者可以忽略不计，总时间复杂度为 $O(m^2 \cdot \alpha(n))$。

• 空间复杂度：$O(m + n)$。在进行排序时，我们必须要额外存储每条边原始的编号，用来返回答案，空间复杂度为 $O(m)$。$\texttt{Kruskal}$ 算法中的并查集需要使用 $O(n)$ 的空间，因此总空间复杂度为 $O(m+n)$。

方法二：连通性 + 最小生成树性质

前言

要理解方法二，读者必须要知道最小生成树的一个性质：

• 在 $\texttt{Kruskal}$ 算法中，对于任意的实数 $w$，只要我们将给定的边按照权值从小到大进行排序，那么当我们按照顺序处理完所有权值小于等于 $w$ 的边之后，对应的并查集的连通性是唯一确定的，无论我们在排序时如何规定权值相同的边的顺序。

并且读者需要掌握：

• 给定一个无向图，使用 $\texttt{Tarjan}$ 算法求出所有的桥边。

思路与算法

假设我们已经处理完了所有权值小于 $w$ 的边，并查集的状态记为 $U$，该状态是唯一确定的。此时，我们同时处理所有权值等于 $w$ 的边，记这些边的集合为 ${e_w}$。我们将 $U$ 中的每一个连通分量看成一个节点，对于 ${e_w}$ 中的每一条无向边的两个端点，将它们在 $U$ 中属于的连通分量对应的节点之间连接一条无向边，以此得到图 $G$。图 $G$ 中会有三种类型的边：

• 自环边：即从一个节点指向本身的一条边。如果 ${e_w}$ 中的一条边的两个端点属于同一个连通分量，那么它在图 $G$ 中表现为一条自环边。根据 $\texttt{Kruskal}$ 算法，这样的边不会被添加进最小生成树中。

对于剩余的边，它们的两个端点属于不同的联通分量。如果我们将其作为 $\texttt{Kruskal}$ 算法中第一条权值为 $w$ 的边进行处理，那么这条边一定会被添加进最小生成树中。因此剩余的边要么是关键边，要么是伪关键边，它们在图 $G$ 中的表现形式不同：

• 桥边。如果 ${e_w}$ 中的一条边对应了图 $G$ 中的一条桥边，那么当这条边被删去时，图 $G$ 的连通性就会发生改变。

  这样的例子可能会帮助理解：如果我们将这条边作为 $\texttt{Kruskal}$ 算法中最后一条权值为 $w$ 的边进行处理，那么这条边还是会被添加进最小生成树中。

  也就是说，这条边对于最小生成树而言是必须的，那么它就是关键边；

• 非桥边。如果 ${e_w}$ 中的一条边对应了图 $G$ 中的一条非桥边，那么当这条边被删去时，图 $G$ 的连通性不会发生改变。

  这样的例子可能会帮助理解：如果我们将这条边作为 $\texttt{Kruskal}$ 算法中最后一条权值为 $w$ 的边进行处理，那么在此之前，并查集的连通性已经和（任意顺序）处理完所有权值为 $w$ 的边之后的连通性一致，这条边就不会被添加进最小生成树中。

  也就是说，这条边对于最小生成树而言不是必须的，那么它就是伪关键边。

因此图 $G$ 中的桥边与 ${e_w}$ 中的关键边一一对应，非桥边（且非自环边）与 ${e_w}$ 中的非关键边一一对应。

我们可以使用 $\texttt{Tarjan}$ 算法求出图 $G$ 中的所有桥边，那么算法的时间复杂度是多少呢？如果图 $G$ 中有 $n_0$ 个节点和 $m_0$ 条边，那么 $\texttt{Tarjan}$ 算法的时间复杂度为 $O(n_0 + m_0)$。对于每一个 $w$ 值对应的 ${e_w}$，我们并不需要将并查集中的每一个连通分量都作为一个节点放入图 $G$ 中：即如果 ${e_w}$ 中包含 $m_0$ 条边，那么它们最多会只连接了 $2m_0$ 个连通分量，因此图 $G$ 中最多有 $2m_0$ 个节点和 $m_0$ 条边（如果一条边是自环边，那么也不需要将其放入图 $G$ 中），时间复杂度为 $O(2m_0 + m_0) = O(m_0)$，与 ${e_w}$ 中包含的边数成正比。我们对所有的 $w$ 值都需要进行一次 $\texttt{Tarjan}$ 算法，这部分的总时间复杂度是 $O(m)$。对于排序的部分，时间复杂度是 $O(m \log m)$，对于并查集的部分，时间复杂度是 $O(m \cdot \alpha(n))$，其中 $\alpha$ 是阿克曼函数的反函数。三者中排序的时间复杂度在渐进意义下最大，因此总时间复杂度为 $O(m \log m)$。

代码

[sol2-C++]
// 并查集模板
class UnionFind {
public:
    vector<int> parent;
    vector<int> size;
    int n;
    // 当前连通分量数目
    int setCount;
    
public:
    UnionFind(int _n): n(_n), setCount(_n), parent(_n), size(_n, 1) {
        iota(parent.begin(), parent.end(), 0);
    }
    
    int findset(int x) {
        return parent[x] == x ? x : parent[x] = findset(parent[x]);
    }
    
    bool unite(int x, int y) {
        x = findset(x);
        y = findset(y);
        if (x == y) {
            return false;
        }
        if (size[x] < size[y]) {
            swap(x, y);
        }
        parent[y] = x;
        size[x] += size[y];
        --setCount;
        return true;
    }
    
    bool connected(int x, int y) {
        x = findset(x);
        y = findset(y);
        return x == y;
    }
};

// Tarjan 算法求桥边模版
class TarjanSCC {
private:
    const vector<vector<int>>& edges;
    const vector<vector<int>>& edgesId;
    vector<int> low;
    vector<int> dfn;
    vector<int> ans;
    int n;
    int ts;

private:
    void getCuttingEdge_(int u, int parentEdgeId) {
        low[u] = dfn[u] = ++ts;
        for (int i = 0; i < edges[u].size(); ++i) {
            int v = edges[u][i];
            int id = edgesId[u][i];
            if (dfn[v] == -1) {
                getCuttingEdge_(v, id);
                low[u] = min(low[u], low[v]);
                if (low[v] > dfn[u]) {
                    ans.push_back(id);
                }
            }
            else if (id != parentEdgeId) {
                low[u] = min(low[u], dfn[v]);
            }
        }
    }

public:
    TarjanSCC(int n_, const vector<vector<int>>& edges_, const vector<vector<int>>& edgesId_): \
        edges(edges_), edgesId(edgesId_), low(n_, -1), dfn(n_, -1), n(n_), ts(-1) {}
    
    vector<int> getCuttingEdge() {
        for (int i = 0; i < n; ++i) {
            if (dfn[i] == -1) {
                getCuttingEdge_(i, -1);
            }
        }
        return ans;
    }
};

class Solution {
public:
    vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges) {
        int m = edges.size();
        for (int i = 0; i < m; ++i) {
            edges[i].push_back(i);
        }
        sort(edges.begin(), edges.end(), [](const auto& u, const auto& v) {
            return u[2] < v[2];
        });

        UnionFind uf(n);
        vector<vector<int>> ans(2);
        vector<int> label(m);
        for (int i = 0; i < m;) {
            // 找出所有权值为 w 的边，下标范围为 [i, j)
            int w = edges[i][2];
            int j = i;
            while (j < m && edges[j][2] == edges[i][2]) {
                ++j;
            }

            // 存储每个连通分量在图 G 中的编号
            unordered_map<int, int> compToId;
            // 图 G 的节点数
            int gn = 0;
            
            for (int k = i; k < j; ++k) {
                int x = uf.findset(edges[k][0]);
                int y = uf.findset(edges[k][1]);
                if (x != y) {
                    if (!compToId.count(x)) {
                        compToId[x] = gn++;
                    }
                    if (!compToId.count(y)) {
                        compToId[y] = gn++;
                    }
                }
                else {
                    // 将自环边标记为 -1
                    label[edges[k][3]] = -1;
                }
            }
            
            // 图 G 的边
            vector<vector<int>> gm(gn), gmid(gn);
            
            for (int k = i; k < j; ++k) {
                int x = uf.findset(edges[k][0]);
                int y = uf.findset(edges[k][1]);
                if (x != y) {
                    int idx = compToId[x], idy = compToId[y];
                    gm[idx].push_back(idy);
                    gmid[idx].push_back(edges[k][3]);
                    gm[idy].push_back(idx);
                    gmid[idy].push_back(edges[k][3]);
                }
            }

            vector<int> bridges = TarjanSCC(gn, gm, gmid).getCuttingEdge();
            // 将桥边（关键边）标记为 1
            for (int id: bridges) {
                ans[0].push_back(id);
                label[id] = 1;
            }

            for (int k = i; k < j; ++k) {
                uf.unite(edges[k][0], edges[k][1]);
            }

            i = j;
        }

        // 未标记的边即为非桥边（伪关键边）
        for (int i = 0; i < m; ++i) {
            if (!label[i]) {
                ans[1].push_back(i);
            }
        }

        return ans;
    }
};

[sol2-Java]
class Solution {
    public List<List<Integer>> findCriticalAndPseudoCriticalEdges(int n, int[][] edges) {
        int m = edges.length;
        int[][] newEdges = new int[m][4];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < 3; ++j) {
                newEdges[i][j] = edges[i][j];
            }
            newEdges[i][3] = i;
        }
        Arrays.sort(newEdges, new Comparator<int[]>() {
            public int compare(int[] u, int[] v) {
                return u[2] - v[2];
            }
        });

        UnionFind uf = new UnionFind(n);
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        for (int i = 0; i < 2; ++i) {
            ans.add(new ArrayList<Integer>());
        }
        int[] label = new int[m];
        for (int i = 0; i < m;) {
            // 找出所有权值为 w 的边，下标范围为 [i, j)
            int w = newEdges[i][2];
            int j = i;
            while (j < m && newEdges[j][2] == newEdges[i][2]) {
                ++j;
            }

            // 存储每个连通分量在图 G 中的编号
            Map<Integer, Integer> compToId = new HashMap<Integer, Integer>();
            // 图 G 的节点数
            int gn = 0;
            
            for (int k = i; k < j; ++k) {
                int x = uf.findset(newEdges[k][0]);
                int y = uf.findset(newEdges[k][1]);
                if (x != y) {
                    if (!compToId.containsKey(x)) {
                        compToId.put(x, gn++);
                    }
                    if (!compToId.containsKey(y)) {
                        compToId.put(y, gn++);
                    }
                } else {
                    // 将自环边标记为 -1
                    label[newEdges[k][3]] = -1;
                }
            }
            
            // 图 G 的边
            List<Integer>[] gm = new List[gn];
            List<Integer>[] gmid = new List[gn];
            for (int k = 0; k < gn; ++k) {
                gm[k] = new ArrayList<Integer>();
                gmid[k] = new ArrayList<Integer>();
            }
            
            for (int k = i; k < j; ++k) {
                int x = uf.findset(newEdges[k][0]);
                int y = uf.findset(newEdges[k][1]);
                if (x != y) {
                    int idx = compToId.get(x), idy = compToId.get(y);
                    gm[idx].add(idy);
                    gmid[idx].add(newEdges[k][3]);
                    gm[idy].add(idx);
                    gmid[idy].add(newEdges[k][3]);
                }
            }

            List<Integer> bridges = new TarjanSCC(gn, gm, gmid).getCuttingEdge();
            // 将桥边（关键边）标记为 1
            for (int id : bridges) {
                ans.get(0).add(id);
                label[id] = 1;
            }

            for (int k = i; k < j; ++k) {
                uf.unite(newEdges[k][0], newEdges[k][1]);
            }

            i = j;
        }

        // 未标记的边即为非桥边（伪关键边）
        for (int i = 0; i < m; ++i) {
            if (label[i] == 0) {
                ans.get(1).add(i);
            }
        }

        return ans;
    }
}

// 并查集模板
class UnionFind {
    int[] parent;
    int[] size;
    int n;
    // 当前连通分量数目
    int setCount;

    public UnionFind(int n) {
        this.n = n;
        this.setCount = n;
        this.parent = new int[n];
        this.size = new int[n];
        Arrays.fill(size, 1);
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }
    
    public int findset(int x) {
        return parent[x] == x ? x : (parent[x] = findset(parent[x]));
    }
    
    public boolean unite(int x, int y) {
        x = findset(x);
        y = findset(y);
        if (x == y) {
            return false;
        }
        if (size[x] < size[y]) {
            int temp = x;
            x = y;
            y = temp;
        }
        parent[y] = x;
        size[x] += size[y];
        --setCount;
        return true;
    }
    
    public boolean connected(int x, int y) {
        x = findset(x);
        y = findset(y);
        return x == y;
    }
}

class TarjanSCC {
    List<Integer>[] edges;
    List<Integer>[] edgesId;
    int[] low;
    int[] dfn;
    List<Integer> ans;
    int n;
    int ts;

    public TarjanSCC(int n, List<Integer>[] edges, List<Integer>[] edgesId) {
        this.edges = edges;
        this.edgesId = edgesId;
        this.low = new int[n];
        Arrays.fill(low, -1);
        this.dfn = new int[n];
        Arrays.fill(dfn, -1);
        this.n = n;
        this.ts = -1;
        this.ans = new ArrayList<Integer>();
    }
    
    public List<Integer> getCuttingEdge() {
        for (int i = 0; i < n; ++i) {
            if (dfn[i] == -1) {
                getCuttingEdge(i, -1);
            }
        }
        return ans;
    }

    private void getCuttingEdge(int u, int parentEdgeId) {
        low[u] = dfn[u] = ++ts;
        for (int i = 0; i < edges[u].size(); ++i) {
            int v = edges[u].get(i);
            int id = edgesId[u].get(i);
            if (dfn[v] == -1) {
                getCuttingEdge(v, id);
                low[u] = Math.min(low[u], low[v]);
                if (low[v] > dfn[u]) {
                    ans.add(id);
                }
            } else if (id != parentEdgeId) {
                low[u] = Math.min(low[u], dfn[v]);
            }
        }
    }
}

[sol2-Python3]
# 并查集模板
class UnionFind:
    def __init__(self, n: int):
        self.parent = list(range(n))
        self.size = [1] * n
        self.n = n
        # 当前连通分量数目
        self.setCount = n
    
    def findset(self, x: int) -> int:
        if self.parent[x] == x:
            return x
        self.parent[x] = self.findset(self.parent[x])
        return self.parent[x]
    
    def unite(self, x: int, y: int) -> bool:
        x, y = self.findset(x), self.findset(y)
        if x == y:
            return False
        if self.size[x] < self.size[y]:
            x, y = y, x
        self.parent[y] = x
        self.size[x] += self.size[y]
        self.setCount -= 1
        return True
    
    def connected(self, x: int, y: int) -> bool:
        x, y = self.findset(x), self.findset(y)
        return x == y

# Tarjan 算法求桥边模版
class TarjanSCC:
    def __init__(self, n: int, edges: List[List[int]], edgesId: List[List[int]]):
        self.n = n
        self.edges = edges
        self.edgesId = edgesId
        self.low = [-1] * n
        self.dfn = [-1] * n
        self.ans = list()
        self.ts = -1
    
    def getCuttingEdge(self) -> List[int]:
        for i in range(self.n):
            if self.dfn[i] == -1:
                self.pGetCuttingEdge(i, -1)
        return self.ans
    
    def pGetCuttingEdge(self, u: int, parentEdgeId: int):
        self.ts += 1
        self.low[u] = self.dfn[u] = self.ts
        for v, iden in zip(self.edges[u], self.edgesId[u]):
            if self.dfn[v] == -1:
                self.pGetCuttingEdge(v, iden)
                self.low[u] = min(self.low[u], self.low[v])
                if self.low[v] > self.dfn[u]:
                    self.ans.append(iden)
            elif iden != parentEdgeId:
                self.low[u] = min(self.low[u], self.dfn[v])

class Solution:
    def findCriticalAndPseudoCriticalEdges(self, n: int, edges: List[List[int]]) -> List[List[int]]:
        m = len(edges)
        for i, edge in enumerate(edges):
            edge.append(i)
        edges.sort(key=lambda x: x[2])

        uf = UnionFind(n)
        ans0 = list()
        label = [0] * m

        i = 0
        while i < m:
            # 找出所有权值为 w 的边，下标范围为 [i, j)
            w = edges[i][2]
            j = i
            while j < m and edges[j][2] == edges[i][2]:
                j += 1

            # 存储每个连通分量在图 G 中的编号
            compToId = dict()
            # 图 G 的节点数
            gn = 0
            
            for k in range(i, j):
                x = uf.findset(edges[k][0])
                y = uf.findset(edges[k][1])
                if x != y:
                    if x not in compToId:
                        compToId[x] = gn
                        gn += 1
                    if y not in compToId:
                        compToId[y] = gn
                        gn += 1
                else:
                    # 将自环边标记为 -1
                    label[edges[k][3]] = -1
            
            # 图 G 的边
            gm = collections.defaultdict(list)
            gmid = collections.defaultdict(list)
            
            for k in range(i, j):
                x = uf.findset(edges[k][0])
                y = uf.findset(edges[k][1])
                if x != y:
                    idx, idy = compToId[x], compToId[y]
                    gm[idx].append(idy)
                    gmid[idx].append(edges[k][3])
                    gm[idy].append(idx)
                    gmid[idy].append(edges[k][3])

            bridges = TarjanSCC(gn, gm, gmid).getCuttingEdge()
            # 将桥边（关键边）标记为 1
            ans0.extend(bridges)
            for iden in bridges:
                label[iden] = 1

            for k in range(i, j):
                uf.unite(edges[k][0], edges[k][1])
            
            i = j

        # 未标记的边即为非桥边（伪关键边）
        ans1 = [i for i in range(m) if label[i] == 0]

        return [ans0, ans1]

[sol2-Golang]
type unionFind struct {
    parent, size []int
}

func newUnionFind(n int) *unionFind {
    parent := make([]int, n)
    size := make([]int, n)
    for i := range parent {
        parent[i] = i
        size[i] = 1
    }
    return &unionFind{parent, size}
}

func (uf *unionFind) find(x int) int {
    if uf.parent[x] != x {
        uf.parent[x] = uf.find(uf.parent[x])
    }
    return uf.parent[x]
}

func (uf *unionFind) union(x, y int) bool {
    fx, fy := uf.find(x), uf.find(y)
    if fx == fy {
        return false
    }
    if uf.size[fx] < uf.size[fy] {
        fx, fy = fy, fx
    }
    uf.size[fx] += uf.size[fy]
    uf.parent[fy] = fx
    return true
}

func findCriticalAndPseudoCriticalEdges(n int, edges [][]int) [][]int {
    m := len(edges)
    edgeType := make([]int, m) // -1：不在最小生成树中；0：伪关键边；1：关键边

    for i, e := range edges {
        edges[i] = append(e, i)
    }
    sort.Slice(edges, func(i, j int) bool { return edges[i][2] < edges[j][2] })

    type neighbor struct{ to, edgeID int }
    graph := make([][]neighbor, n)
    dfn := make([]int, n) // 遍历到该顶点时的时间戳
    timestamp := 0
    var tarjan func(int, int) int
    tarjan = func(v, pid int) int {
        timestamp++
        dfn[v] = timestamp
        lowV := timestamp
        for _, e := range graph[v] {
            if w := e.to; dfn[w] == 0 {
                lowW := tarjan(w, e.edgeID)
                if lowW > dfn[v] {
                    edgeType[e.edgeID] = 1
                }
                lowV = min(lowV, lowW)
            } else if e.edgeID != pid {
                lowV = min(lowV, dfn[w])
            }
        }
        return lowV
    }

    uf := newUnionFind(n)
    for i := 0; i < m; {
        vs := []int{}
        // 将权值相同的边分为一组，建图，然后用 Tarjan 算法找桥边
        for weight := edges[i][2]; i < m && edges[i][2] == weight; i++ {
            e := edges[i]
            v, w, edgeID := uf.find(e[0]), uf.find(e[1]), e[3]
            if v != w {
                graph[v] = append(graph[v], neighbor{w, edgeID})
                graph[w] = append(graph[w], neighbor{v, edgeID})
                vs = append(vs, v, w) // 记录图中顶点
            } else {
                edgeType[edgeID] = -1
            }
        }
        for _, v := range vs {
            if dfn[v] == 0 {
                tarjan(v, -1)
            }
        }
        // 合并顶点、重置数据
        for j := 0; j < len(vs); j += 2 {
            v, w := vs[j], vs[j+1]
            uf.union(v, w)
            graph[v] = nil
            graph[w] = nil
            dfn[v] = 0
            dfn[w] = 0
        }
    }

    var keyEdges, pseudokeyEdges []int
    for i, tp := range edgeType {
        if tp == 0 {
            pseudokeyEdges = append(pseudokeyEdges, i)
        } else if tp == 1 {
            keyEdges = append(keyEdges, i)
        }
    }
    return [][]int{keyEdges, pseudokeyEdges}
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

复杂度分析

• 时间复杂度：$O(m \log m)$，其中 $m$ 是图中的边数。

• 空间复杂度：$O(m + n)$。排序时存储每条边原始编号的空间为 $O(m)$，并查集使用的空间为 $O(n)$，$\texttt{Tarjan}$ 算法使用的总空间为 $O(m)$。

统计信息

通过次数	提交次数	AC比率
11700	16963	69.0%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言