原文链接: https://leetcode-cn.com/problems/parallel-courses-ii

英文原文

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei. Also, you are given the integer k.

In one semester, you can take at most k courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.

Return the minimum number of semesters needed to take all courses. The testcases will be generated such that it is possible to take every course.

 

Example 1:

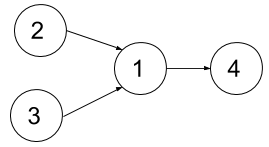
Input: n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2
Output: 3 
Explanation: The figure above represents the given graph.
In the first semester, you can take courses 2 and 3.
In the second semester, you can take course 1.
In the third semester, you can take course 4.

Example 2:

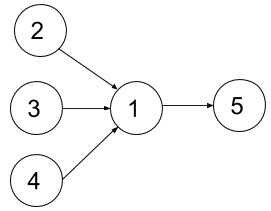
Input: n = 5, dependencies = [[2,1],[3,1],[4,1],[1,5]], k = 2
Output: 4 
Explanation: The figure above represents the given graph.
In the first semester, you can take courses 2 and 3 only since you cannot take more than two per semester.
In the second semester, you can take course 4.
In the third semester, you can take course 1.
In the fourth semester, you can take course 5.

Example 3:

Input: n = 11, dependencies = [], k = 2
Output: 6

 

Constraints:

• 1 <= n <= 15
• 1 <= k <= n
• 0 <= relations.length <= n * (n-1) / 2
• relations[i].length == 2
• 1 <= prevCoursei, nextCoursei <= n
• prevCoursei != nextCoursei
• All the pairs [prevCoursei, nextCoursei] are unique.
• The given graph is a directed acyclic graph.

中文题目

给你一个整数 n 表示某所大学里课程的数目，编号为 1 到 n ，数组 dependencies 中， dependencies[i] = [xi, yi]  表示一个先修课的关系，也就是课程 xi 必须在课程 yi 之前上。同时你还有一个整数 k 。

在一个学期中，你 最多 可以同时上 k 门课，前提是这些课的先修课在之前的学期里已经上过了。

请你返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。

 

示例 1：

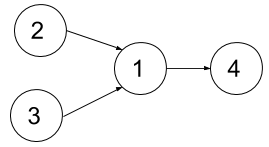
输入：n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2
输出：3 
解释：上图展示了题目输入的图。在第一个学期中，我们可以上课程 2 和课程 3 。然后第二个学期上课程 1 ，第三个学期上课程 4 。

示例 2：

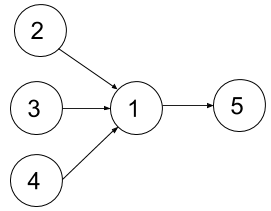
输入：n = 5, dependencies = [[2,1],[3,1],[4,1],[1,5]], k = 2
输出：4 
解释：上图展示了题目输入的图。一个最优方案是：第一学期上课程 2 和 3，第二学期上课程 4 ，第三学期上课程 1 ，第四学期上课程 5 。

示例 3：

输入：n = 11, dependencies = [], k = 2
输出：6

 

提示：

• 1 <= n <= 15
• 1 <= k <= n
• 0 <= dependencies.length <= n * (n-1) / 2
• dependencies[i].length == 2
• 1 <= xi, yi <= n
• xi != yi
• 所有先修关系都是不同的，也就是说 dependencies[i] != dependencies[j] 。
• 题目输入的图是个有向无环图。

通过代码

高赞题解

世界服题目的讨论区全是错误的贪心算法，有点可惜。

不过看到国服这里还都是正确的状压 DP，那我也贡献一下自己的代码吧。

希望国服的题解区不要歪掉。

[sol1-C++]
class Solution {
public:
    int minNumberOfSemesters(int n, vector<vector<int>>& dependencies, int k) {
        vector<int> prereq(n);
        for (const auto& dep: dependencies) {
            prereq[dep[1] - 1] |= (1 << (dep[0] - 1));
        }
        
        vector<int> set_prereq(1 << n), valid(1 << n);
        for (int mask = 0; mask < (1 << n); ++mask) {
            if (__builtin_popcount(mask) <= k) {
                for (int i = 0; i < n; ++i) {
                    if (mask & (1 << i)) {
                        set_prereq[mask] |= prereq[i];
                    }
                }
                valid[mask] = ((set_prereq[mask] & mask) == 0);
            }
        }
        
        vector<int> dp(1 << n, INT_MAX / 2);
        dp[0] = 0;
        for (int mask = 0; mask < (1 << n); ++mask) {
            for (int subset = mask; subset; subset = (subset - 1) & mask) {
                if (valid[subset] && ((mask & set_prereq[subset]) == set_prereq[subset])) {
                    dp[mask] = min(dp[mask], dp[mask ^ subset] + 1);
                }
            }
        }
        return dp[(1 << n) - 1];
    }
};

注：关于状态压缩动态规划，我很久以前在力扣世界服写过一篇 简单的总结，有兴趣的小伙伴可以阅读一下～

统计信息

通过次数	提交次数	AC比率
2358	6315	37.3%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言