原文链接: https://leetcode-cn.com/problems/best-position-for-a-service-centre

英文原文

A delivery company wants to build a new service centre in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new centre in a position such that the sum of the euclidean distances to all customers is minimum.

Given an array positions where positions[i] = [xi, yi] is the position of the ith customer on the map, return the minimum sum of the euclidean distances to all customers.

In other words, you need to choose the position of the service centre [xcentre, ycentre] such that the following formula is minimized:

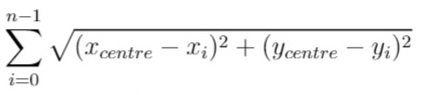
Answers within 10^-5 of the actual value will be accepted.

 

Example 1:

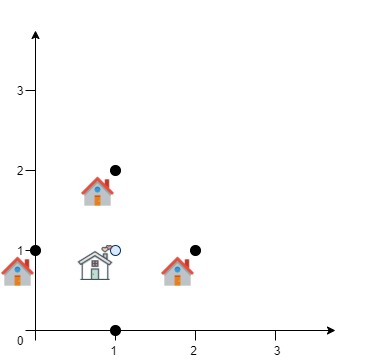
Input: positions = [[0,1],[1,0],[1,2],[2,1]]
Output: 4.00000
Explanation: As shown, you can see that choosing [xcentre, ycentre] = [1, 1] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.

Example 2:

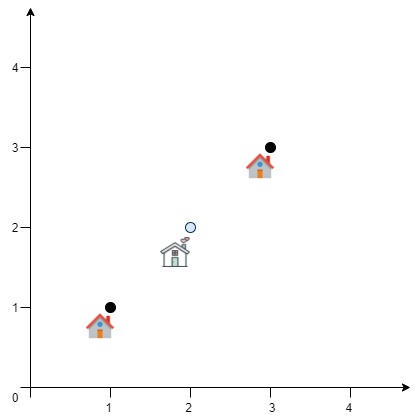
Input: positions = [[1,1],[3,3]]
Output: 2.82843
Explanation: The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843

Example 3:

Input: positions = [[1,1]]
Output: 0.00000

Example 4:

Input: positions = [[1,1],[0,0],[2,0]]
Output: 2.73205
Explanation: At the first glance, you may think that locating the centre at [1, 0] will achieve the minimum sum, but locating it at [1, 0] will make the sum of distances = 3.
Try to locate the centre at [1.0, 0.5773502711] you will see that the sum of distances is 2.73205.
Be careful with the precision!

Example 5:

Input: positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]]
Output: 32.94036
Explanation: You can use [4.3460852395, 4.9813795505] as the position of the centre.

 

Constraints:

• 1 <= positions.length <= 50
• positions[i].length == 2
• 0 <= positions[i][0], positions[i][1] <= 100

中文题目

一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标，并希望能够以此为依据为新的服务中心选址：使服务中心 到所有客户的欧几里得距离的总和最小 。

给你一个数组 positions ，其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置，返回到所有客户的 欧几里得距离的最小总和 。

换句话说，请你为服务中心选址，该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值：

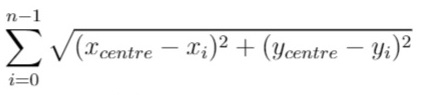
与真实值误差在 10^-5 之内的答案将被视作正确答案。

 

示例 1：

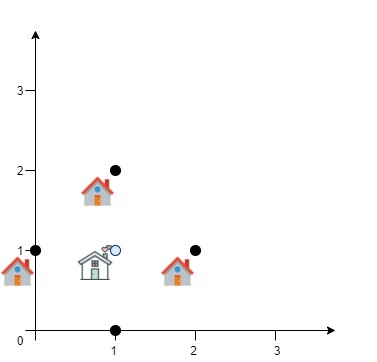
输入：positions = [[0,1],[1,0],[1,2],[2,1]]
输出：4.00000
解释：如图所示，你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置，这样一来到每个客户的距离就都是 1，所有距离之和为 4 ，这也是可以找到的最小值。

示例 2：

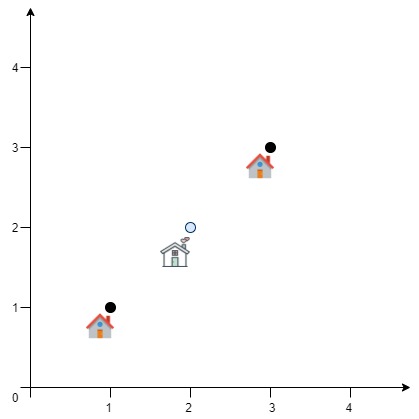
输入：positions = [[1,1],[3,3]]
输出：2.82843
解释：欧几里得距离可能的最小总和为 sqrt(2) + sqrt(2) = 2.82843

示例 3：

输入：positions = [[1,1]]
输出：0.00000

示例 4：

输入：positions = [[1,1],[0,0],[2,0]]
输出：2.73205
解释：乍一看，你可能会将中心定在 [1, 0] 并期待能够得到最小总和，但是如果选址在 [1, 0] 距离总和为 3
如果将位置选在 [1.0, 0.5773502711] ，距离总和将会变为 2.73205
当心精度问题！

示例 5：

输入：positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]]
输出：32.94036
解释：你可以用 [4.3460852395, 4.9813795505] 作为新中心的位置

 

提示：

• 1 <= positions.length <= 50
• positions[i].length == 2
• 0 <= positions[i][0], positions[i][1] <= 100

通过代码

高赞题解

解题思路

先想到如果确定了x，y对应的到各点距离和应该是凸函数；各x对应的最小距离和也是凸函数。在凸函数上查最值点可以用三分查找，这题也就是三分套三分。
三分查找形式如下：

在[l,r]上求f(x)的最小值，每次把范围三等分为[l,m),[m,mm],(mm,r]。不妨设f(m)<f(mm)，必有最小值点x<mm，不可能在(mm,r]上，因为若x>mm，则m、mm、x三点是一个上凸，所以令r=mm删去这一段。

三分是逼近取值，需要确定精度，结果要求保证误差在1e-5以内，计算点时精度要更高一点，就精确到1e-6。

时间复杂度:点取值范围是[0,100]，计算精确到1e-6，三分每次变成2/3，一层三分需要k次迭代满足(100-0)*(2/3)^k<1e-6，解k约为46。计算距离是n。总体时间复杂度O(kkn)。

代码

class Solution:
    def getMinDistSum(self, positions: List[List[int]]) -> float:
        # 到各点距离之和
        def dis(x, y):
            return sum([((px - x) ** 2 + (py - y) ** 2) ** 0.5 for px, py in positions])

        # 三分找最小
        def three_divide(l, r, f, eps=1e-6):
            while r - l > eps:
                m = l + (r - l) / 3
                mm = r - (r - l) / 3
                if f(m) < f(mm):
                    r = mm
                else:
                    l = m
            return f((l + r) / 2)

        # 左右边界
        lmin, rmax = 0, 100

        # 外层查x,x=mx时最小距离
        def xf(mx):
            # 内层查y,x=mx且y=my的距离
            def yf(my): return dis(mx, my)
            return three_divide(lmin, rmax, yf)

        return three_divide(lmin, rmax, xf)

统计信息

通过次数	提交次数	AC比率
3274	9513	34.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言