原文链接: https://leetcode-cn.com/problems/number-of-ways-to-reorder-array-to-get-same-bst

英文原文

Given an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.

For example, given nums = [2,1,3], we will have 2 as the root, 1 as a left child, and 3 as a right child. The array [2,3,1] also yields the same BST but [3,2,1] yields a different BST.

Return the number of ways to reorder nums such that the BST formed is identical to the original BST formed from nums.

Since the answer may be very large, return it modulo 10^9 + 7.

 

Example 1:

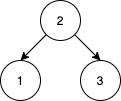
Input: nums = [2,1,3]
Output: 1
Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.

Example 2:

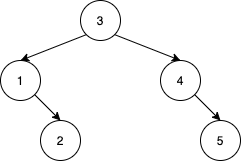
Input: nums = [3,4,5,1,2]
Output: 5
Explanation: The following 5 arrays will yield the same BST: 
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
[3,4,1,2,5]
[3,4,1,5,2]

Example 3:

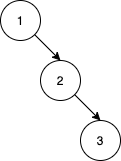
Input: nums = [1,2,3]
Output: 0
Explanation: There are no other orderings of nums that will yield the same BST.

Example 4:

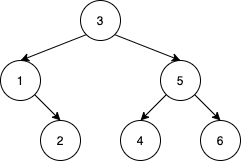
Input: nums = [3,1,2,5,4,6]
Output: 19

Example 5:

Input: nums = [9,4,2,1,3,6,5,7,8,14,11,10,12,13,16,15,17,18]
Output: 216212978
Explanation: The number of ways to reorder nums to get the same BST is 3216212999. Taking this number modulo 10^9 + 7 gives 216212978.

 

Constraints:

• 1 <= nums.length <= 1000
• 1 <= nums[i] <= nums.length
• All integers in nums are distinct.

中文题目

给你一个数组 nums 表示 1 到 n 的一个排列。我们按照元素在 nums 中的顺序依次插入一个初始为空的二叉查找树（BST）。请你统计将 nums 重新排序后，统计满足如下条件的方案数：重排后得到的二叉查找树与 nums 原本数字顺序得到的二叉查找树相同。

比方说，给你 nums = [2,1,3]，我们得到一棵 2 为根，1 为左孩子，3 为右孩子的树。数组 [2,3,1] 也能得到相同的 BST，但 [3,2,1] 会得到一棵不同的 BST 。

请你返回重排 nums 后，与原数组 nums 得到相同二叉查找树的方案数。

由于答案可能会很大，请将结果对 10^9 + 7 取余数。

 

示例 1：

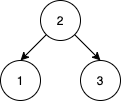
输入：nums = [2,1,3]
输出：1
解释：我们将 nums 重排， [2,3,1] 能得到相同的 BST 。没有其他得到相同 BST 的方案了。

示例 2：

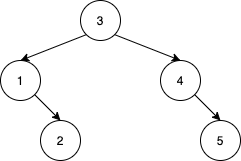
输入：nums = [3,4,5,1,2]
输出：5
解释：下面 5 个数组会得到相同的 BST：
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
[3,4,1,2,5]
[3,4,1,5,2]

示例 3：

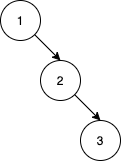
输入：nums = [1,2,3]
输出：0
解释：没有别的排列顺序能得到相同的 BST 。

示例 4：

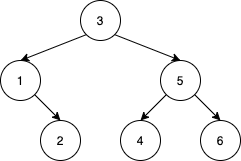
输入：nums = [3,1,2,5,4,6]
输出：19

示例  5：

输入：nums = [9,4,2,1,3,6,5,7,8,14,11,10,12,13,16,15,17,18]
输出：216212978
解释：得到相同 BST 的方案数是 3216212999。将它对 10^9 + 7 取余后得到 216212978。

 

提示：

• 1 <= nums.length <= 1000
• 1 <= nums[i] <= nums.length
• nums 中所有数 互不相同 。

通过代码

高赞题解

5502. 将子数组重新排序得到同一个二叉查找树的方案数

知识点：二叉搜索树；排列组合

二叉查找树，又称二叉排序树，二叉搜索树。其特点是，右子树中的元素都小于根节点，左子树的元素都大于根节点，且左右子树也都是二叉搜索树。当构造一棵二叉搜索树时，第一个插入的元素必然是根节点，其后插入的元素根据与根节点的大小关系被插入到左子树或右子树。

由此可知，如果两种排列对应的二叉搜索树相同，那么必然第一个元素是相同的。

设，小于第一个的元素构成的序列为 less，大于第一个的元素构成的序列为 greater。在不修改 less，greater 内部顺序的前提下，调整 less + greater 这个大序列的顺序，就能得到一个可以构造相同二叉树的新序列。

换个说法，less 的顺序确定了元素插入左子树的顺序，同样的，greater 确定了元素插入右子树的顺序。至于，是先构造左子树还是构造右子树，并不重要。所以 less + greater 的顺序可以调整。

那为何 less 和 greater 的内部顺序不能调整呢？其实不是不能调整，而是要放到构造左右子树的时候再去调整。

那么，还剩最后一个问题，less + greater，一共有多少符合要求排列方式呢？答案为 $C^{less.size()}_{less.size() + greater.size()}$。也就是说，一共有 x 个坑，先选出一部分放 less，剩下的放 greater。

最后将每个子树的组合数累乘即可。

const int64_t mod = 1000000007;
class Solution {
public:
    int64_t com[1001][1001];
    int64_t combine(int a, int b) {
        //cout << a << " " << b << " " << com[a][b] << endl;
        return com[a][b];
    }
    void dfs(const vector<int> &num, int L, int R, int64_t &mul) {
        if(R-L+1 <= 2) {
            return;
        }
        vector<int> less, greater;
        for(int i = L+1; i <= R; i++) {
            if(num[i] < num[L]) {
                less.push_back(num[i]);
            } else {
                greater.push_back(num[i]);
            }
        }
        mul *= combine(greater.size() + less.size(), greater.size());
        if(mul >= mod) {
            mul %= mod;
        }
        dfs(less, 0, less.size()-1, mul);
        dfs(greater, 0, greater.size()-1, mul);
    }
    int numOfWays(vector<int>& nums) {
        //C(n,m)=C(n-1,m)+C(n-1,m-1)
        com[1][0]=com[1][1]=1;
        for(int i=2;i<=1000;i++){
            com[i][0]=1;
            for(int j=1;j<=i;j++)
                com[i][j]=(com[i-1][j]+com[i-1][j-1]) % mod;
        }
        
        int64_t mul = 1;
        dfs(nums, 0, nums.size()-1, mul);
        return (mul - 1 + mod) % mod;
    }
};

如果感觉有点意思，那就关注一下【我的公众号】吧~

统计信息

通过次数	提交次数	AC比率
2133	4483	47.6%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言