1579-保证图可完全遍历(Remove Max Number of Edges to Keep Graph Fully Traversable)

原文链接: https://leetcode-cn.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable

英文原文

Alice and Bob have an undirected graph of n nodes and 3 types of edges:

Type 1: Can be traversed by Alice only.
Type 2: Can be traversed by Bob only.
Type 3: Can by traversed by both Alice and Bob.

Given an array edges where edges[i] = [type_i, u_i, v_i] represents a bidirectional edge of type type_i between nodes u_i and v_i, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.

Return the maximum number of edges you can remove, or return -1 if it's impossible for the graph to be fully traversed by Alice and Bob.

Example 1:

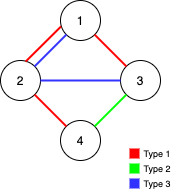
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
Output: 2
Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.

Example 2:

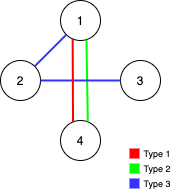
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
Output: 0
Explanation: Notice that removing any edge will not make the graph fully traversable by Alice and Bob.

Example 3:

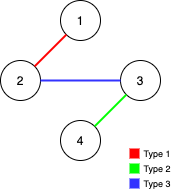
Input: n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
Output: -1
Explanation: In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.

Constraints:

1 <= n <= 10^5
1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
edges[i].length == 3
1 <= edges[i][0] <= 3
1 <= edges[i][1] < edges[i][2] <= n
All tuples (type_i, u_i, v_i) are distinct.

中文题目

Alice 和 Bob 共有一个无向图，其中包含 n 个节点和 3 种类型的边：

类型 1：只能由 Alice 遍历。
类型 2：只能由 Bob 遍历。
类型 3：Alice 和 Bob 都可以遍历。

给你一个数组 edges ，其中 edges[i] = [type_i, u_i, v_i] 表示节点 u_i 和 v_i 之间存在类型为 type_i 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下，找出可以删除的最大边数。如果从任何节点开始，Alice 和 Bob 都可以到达所有其他节点，则认为图是可以完全遍历的。

返回可以删除的最大边数，如果 Alice 和 Bob 无法完全遍历图，则返回 -1 。

示例 1：

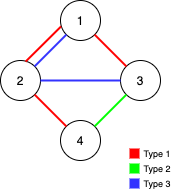
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出：2
解释：如果删除 [1,1,2] 和 [1,1,3] 这两条边，Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。

示例 2：

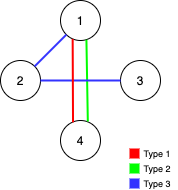
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出：0
解释：注意，删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。

示例 3：

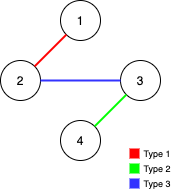
输入：n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出：-1
解释：在当前图中，Alice 无法从其他节点到达节点 4 。类似地，Bob 也不能达到节点 1 。因此，图无法完全遍历。

提示：

1 <= n <= 10^5
1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
edges[i].length == 3
1 <= edges[i][0] <= 3
1 <= edges[i][1] < edges[i][2] <= n
所有元组 (type_i, u_i, v_i) 互不相同

通过代码

高赞题解

解题思路：

首先判断 Alice 和 Bob 的是不是连通图，若都为连通图：

1.考虑单个用户，共有 n 个结点，产生连通图需要的最少边数为 n-1，假设该用户可以访问的边有 m 条，那么多余的为 m-(n-1)

2.现在考虑两个用户，结点为 n 个，两个用户各自可以访问的边数为 p,q（不包含第三种类型的边），其中第三种类型的边为 K1 条

假设最终的连通图对两个用户分别而言都是连通的，且无回路（对单个用户而言），并且用了 K2 条第三种类型的边（无多余的，即这 K2 条第三种类型的边不构成回路），有 K2<=K1，则有：

a.对于第一个用户，多余的边为 p-(n-1-K2),其中 n-1-K2 为，对于第一个用户，还需要多少条只有第一个用户可以访问的边才能构成连通图

b.对于第二个用户，多余的边为 q-(n-1-K2)，其中 n-1-K2 为，对于第二个用户，还需要多少条只有第二个用户可以访问的边才能构成连通图

那么总的多余边(需删除的)为 p-(n-1-K2)+q-(n-1-K2)+(K1-K2) = p+q-2n+2+K1+K2;
由于 p,q,n,K1 为定数，所以要想删除的边最多，那么必须要求最终的图中第三种类型的边 K2 最多，且无多余

因此，可以先添加第三种类型的边，先在第三种类型的边中去除多余的，然后再在剩下的各自可以访问的边中去除多余的

[]
class Solution {
public:
    vector<int> par;
    int cnt;
    int getRoot(int x){
        int root = x;
        while(par[root]!=root){
            root = par[root];
        }
        while(par[x]!=root){
            int tmp = par[x];
            par[x] = root;
            x = tmp;
        }
        return root;
    }
    void merge(int x,int y){
        int _x = getRoot(x);
        int _y = getRoot(y);
        if(_x!=_y){
            par[_x]=_y;
            cnt--;
        }
    }
    //初始化
    void init(int n){
        //cnt为集合个数，初始化每个结点视为一个集合
        cnt = n;
        for(int i =1;i<=n;i++){
            par[i] = i;
        }
    }
    int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
        par = vector<int>(n+1,0);
        int ans = 0;
        //分别存储第一种到第三种类型的边
        int cnt1 = 0,cnt2 = 0,cnt3 = 0;
        init(n);
        //判断对于Alice是否连通
        for(int i = 0;i<edges.size();i++){
            if(edges[i][0]==1||edges[i][0]==3){
                merge(edges[i][1],edges[i][2]);
                cnt1++;
            }
        }
        if(cnt!=1)
            return -1;
        init(n);
        //判断对于Bob是否连通
        for(int i = 0;i<edges.size();i++){
            if(edges[i][0]==2||edges[i][0]==3){
                merge(edges[i][1],edges[i][2]);
                cnt2++;
            }
        }
        if(cnt!=1)
            return -1;
        init(n);
        //添加第三种类型的边
        for(int i = 0;i<edges.size();i++){
            if(edges[i][0]==3){
                merge(edges[i][1],edges[i][2]);
                cnt3++;
            }
        }
        //去除第三种类型的边
        cnt1-=cnt3;
        cnt2-=cnt3;
        //多余的第三种类型的边
        ans+=(cnt3-(n-cnt));
        //多余的其余两种类型的边
        ans += cnt1-(cnt-1)+cnt2-(cnt-1);
        
        return ans;
    }
};

简化版：

[]
class Solution {
public:
    int getRoot(vector<int>& par,int x){
        int root = x;
        while(par[root]!=root){
            root = par[root];
        }
        while(par[x]!=root){
            int tmp = par[x];
            par[x] = root;
            x = tmp;
        }
        return root;
    }
    bool merge(vector<int>& par,int x,int y){
        int _x = getRoot(par,x);
        int _y = getRoot(par,y);
        if(_x!=_y){
            par[_x]=_y;
            return true;
        }
        return false;
    }
    int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
        vector<int>par1 = vector<int>(n+1,0);
        vector<int>par2;
        int ans = 0;
        int cnt1 = n,cnt2;
        for(int i =1;i<=n;i++){
            par1[i] = i;
        }
        //先添加第三种类型的边
        for(int i = 0;i<edges.size();i++){
            if(edges[i][0]==3){
                if(!merge(par1,edges[i][1],edges[i][2]))
                    ans++;
                else
                    cnt1--;
            }
        }
        par2 = par1;
        cnt2 = cnt1;
        //再添加其余两种类型的边
        for(int i = 0;i<edges.size();i++){
            if(edges[i][0]==1){
                if(!merge(par1,edges[i][1],edges[i][2]))
                    ans++;
                else
                    cnt1--;
            }else if(edges[i][0]==2){
                if(!merge(par2,edges[i][1],edges[i][2]))
                    ans++;
                else
                    cnt2--;
            }
        }
        if(cnt1!=1||cnt2!=1)
            return -1;
        return ans;
    }
};

统计信息

通过次数	提交次数	AC比率
16288	26293	61.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途