英文原文
There is a strange printer with the following two special requirements:
- On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
- Once the printer has used a color for the above operation, the same color cannot be used again.
You are given a m x n matrix targetGrid, where targetGrid[row][col] is the color in the position (row, col) of the grid.
Return true if it is possible to print the matrix targetGrid, otherwise, return false.
Example 1:
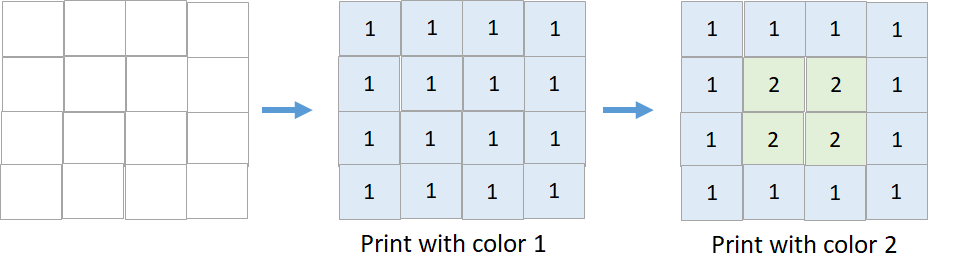
Input: targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]] Output: true
Example 2:
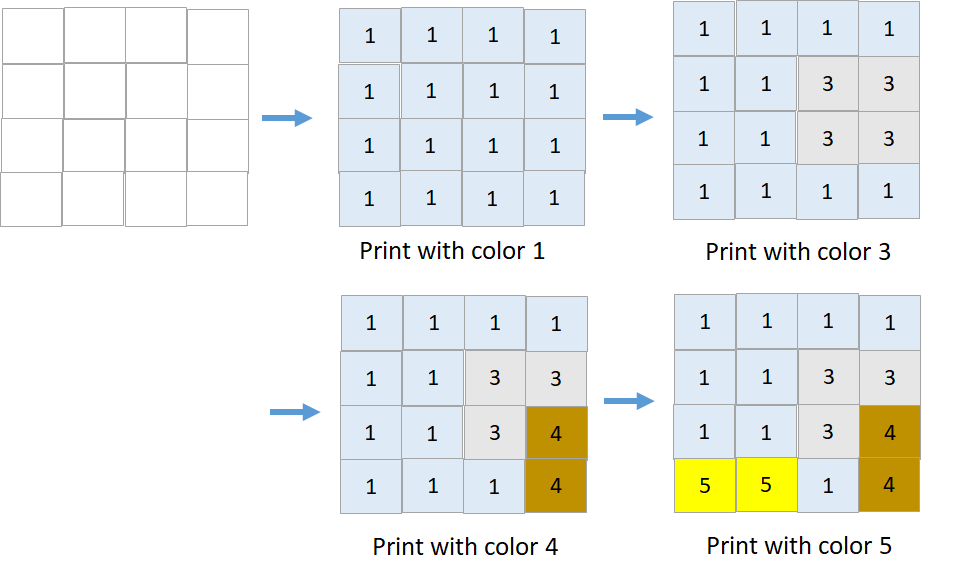
Input: targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]] Output: true
Example 3:
Input: targetGrid = [[1,2,1],[2,1,2],[1,2,1]] Output: false Explanation: It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
Example 4:
Input: targetGrid = [[1,1,1],[3,1,3]] Output: false
Constraints:
m == targetGrid.lengthn == targetGrid[i].length1 <= m, n <= 601 <= targetGrid[row][col] <= 60
中文题目
给你一个奇怪的打印机,它有如下两个特殊的打印规则:
- 每一次操作时,打印机会用同一种颜色打印一个矩形的形状,每次打印会覆盖矩形对应格子里原本的颜色。
- 一旦矩形根据上面的规则使用了一种颜色,那么 相同的颜色不能再被使用 。
给你一个初始没有颜色的 m x n 的矩形 targetGrid ,其中 targetGrid[row][col] 是位置 (row, col) 的颜色。
如果你能按照上述规则打印出矩形 targetGrid ,请你返回 true ,否则返回 false 。
示例 1:
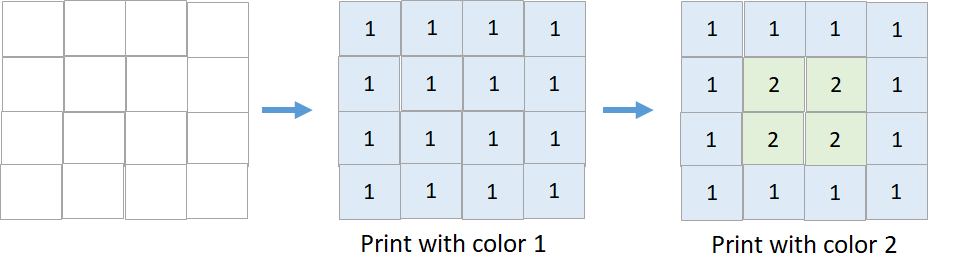
输入:targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]] 输出:true
示例 2:
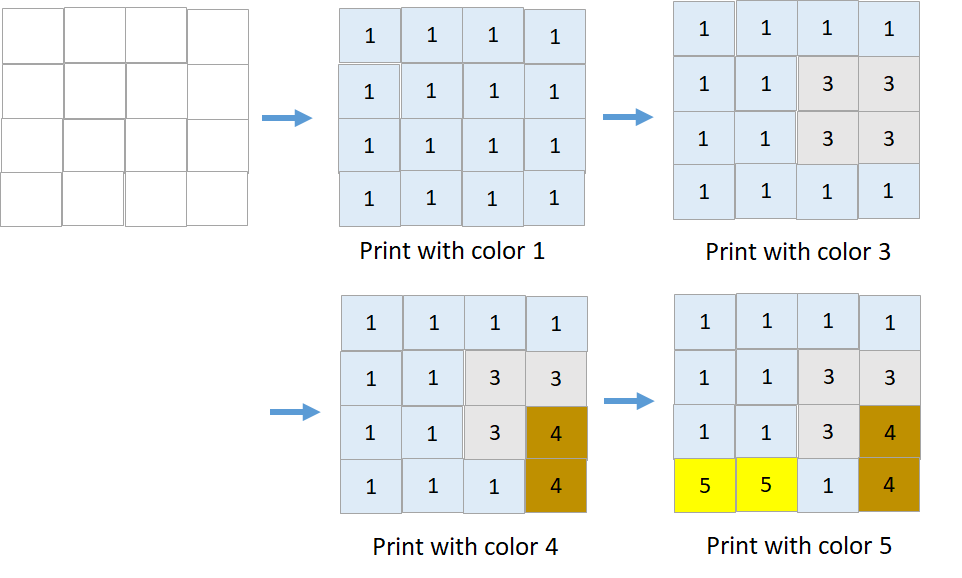
输入:targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]] 输出:true
示例 3:
输入:targetGrid = [[1,2,1],[2,1,2],[1,2,1]] 输出:false 解释:没有办法得到 targetGrid ,因为每一轮操作使用的颜色互不相同。
示例 4:
输入:targetGrid = [[1,1,1],[3,1,3]] 输出:false
提示:
m == targetGrid.lengthn == targetGrid[i].length1 <= m, n <= 601 <= targetGrid[row][col] <= 60
通过代码
高赞题解
这道题可以认为是在研究:是否有一种颜色序列,按照这个序列进行染色,最终矩阵就会呈现输入的状态。
矩形上的某一个像素点,可能会先后经历多次染色。比如先染红,再染绿,再染黄,最后染蓝,最后呈现出的就是蓝色。
我们知道这个像素现在是蓝色;
而它在红色/绿色/黄色矩形范围内,说明这个像素曾经红过/绿过/黄过。
此时我们可以提炼出信息:假定先染的优先于后染的,那么红色优于蓝色,绿色优于蓝色,黄色优于蓝色。
(红绿黄之间的顺序未定)。
题中指出,颜色最多有 $60$ 种,我们可以建立一个有向图,图中的结点就是这 $60$ 个颜色 $1\sim 60$ 。
按照刚才的方法找出所有的有向边,进行拓扑排序即可判断出结果。
class Solution {
public:
bool isPrintable(vector<vector<int>>& t) {
int i,j,k,m,n;
m=t.size();
n=t[0].size();
int top[61],bottom[61],left[61],right[61];
memset(top,0x3f,sizeof(top));
memset(bottom,0xff,sizeof(bottom));
memset(left,0x3f,sizeof(left));
memset(right,0xff,sizeof(right));
//对每种颜色的顶、底、左、右边界进行初始化
for(i=0;i<m;i++){
for(j=0;j<n;j++){
k=t[i][j];
top[k]=min(top[k],i);
bottom[k]=max(bottom[k],i);
left[k]=min(left[k],j);
right[k]=max(right[k],j);
}
}
//遍历矩阵,获取每种颜色的上下左右边界
bool haveedge[61][61]={0};
//haveedge用于避免重复建边
vector<int>edgefrom[61];
//edgefrom[i]表示从i出发的有向边
int rudu[61]={0};
//rudu[i]表示颜色i的入度
for(i=0;i<m;i++){
for(j=0;j<n;j++){
//用i,j做下标遍历图中每个像素
k=t[i][j];
for(int color=1;color<=60;color++){
if(top[color]<=i&&i<=bottom[color]&&left[color]<=j&&j<=right[color]){
if(color!=k&&!haveedge[color][k]){
edgefrom[color].push_back(k);
rudu[k]++;
haveedge[color][k]=true;
}
}
//若t[i][j]位于颜色为color的矩形内部,颜色却不为color为k
//说明先染成color,再染成k
//建立有向边color → k
}
}
}
vector<int>v;
while(true){
for(i=1;i<=60;i++){
if(rudu[i]==0){
v.push_back(i);
rudu[i]=-1;
for(int a:edgefrom[i]){
rudu[a]--;
}
break;
}
}
if(i==61)break;
}
//将入度为0的颜色放入v,最后看1~60是不是都能放入v
return v.size()==60;
}
};统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 1210 | 2083 | 58.1% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




