原文链接: https://leetcode-cn.com/problems/minimum-cost-to-connect-two-groups-of-points

英文原文

You are given two groups of points where the first group has size1 points, the second group has size2 points, and size1 >= size2.

The cost of the connection between any two points are given in an size1 x size2 matrix where cost[i][j] is the cost of connecting point i of the first group and point j of the second group. The groups are connected if each point in both groups is connected to one or more points in the opposite group. In other words, each point in the first group must be connected to at least one point in the second group, and each point in the second group must be connected to at least one point in the first group.

Return the minimum cost it takes to connect the two groups.

 

Example 1:

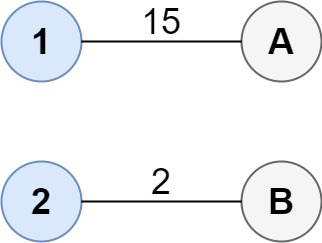
Input: cost = [[15, 96], [36, 2]]
Output: 17
Explanation: The optimal way of connecting the groups is:
1--A
2--B
This results in a total cost of 17.

Example 2:

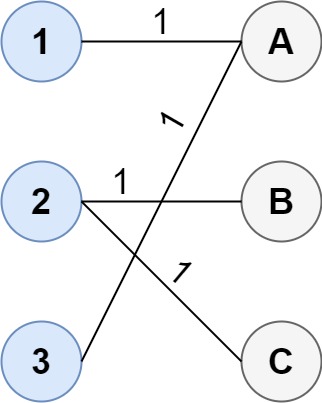
Input: cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
Output: 4
Explanation: The optimal way of connecting the groups is:
1--A
2--B
2--C
3--A
This results in a total cost of 4.
Note that there are multiple points connected to point 2 in the first group and point A in the second group. This does not matter as there is no limit to the number of points that can be connected. We only care about the minimum total cost.

Example 3:

Input: cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
Output: 10

 

Constraints:

• size1 == cost.length
• size2 == cost[i].length
• 1 <= size1, size2 <= 12
• size1 >= size2
• 0 <= cost[i][j] <= 100

中文题目

给你两组点，其中第一组中有 size1 个点，第二组中有 size2 个点，且 size1 >= size2 。

任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出，其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接，则称这两组点是连通的。换言之，第一组中的每个点必须至少与第二组中的一个点连接，且第二组中的每个点必须至少与第一组中的一个点连接。

返回连通两组点所需的最小成本。

 

示例 1：

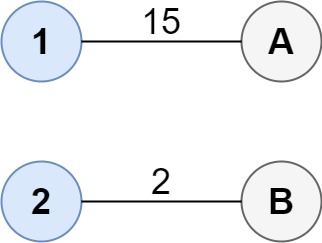
输入：cost = [[15, 96], [36, 2]]
输出：17
解释：连通两组点的最佳方法是：
1--A
2--B
总成本为 17 。

示例 2：

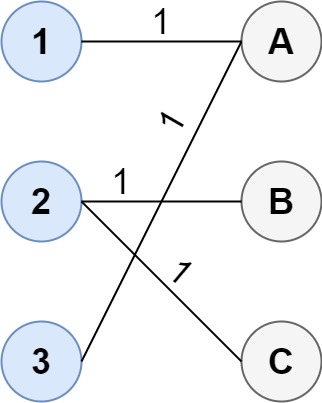
输入：cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出：4
解释：连通两组点的最佳方法是：
1--A
2--B
2--C
3--A
最小成本为 4 。
请注意，虽然有多个点连接到第一组中的点 2 和第二组中的点 A ，但由于题目并不限制连接点的数目，所以只需要关心最低总成本。

示例 3：

输入：cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
输出：10

 

提示：

• size1 == cost.length
• size2 == cost[i].length
• 1 <= size1, size2 <= 12
• size1 >= size2
• 0 <= cost[i][j] <= 100

通过代码

高赞题解

动态规划

问题等价于: 在一个矩阵中选取一些值, 满足矩阵的每一行和每一列都至少有一个元素被选中, 同时选中元素的总和最小 (此矩阵就是 cost 矩阵).

由于矩阵的列数较少, 我们可以用状压 DP 来表示每一行的选取情况, 假设矩阵有 $m$ 行 $n$ 列, 那么我们维护一个 DP 矩阵 dp[m][1 << n], dp[i][j]表示当前选取到第 $i$ 行, 每列的选取状况为 $j$ 时总的最小开销, 其中 $j$ 的第 $k$ 位为 $1$ 即表示第 $k$ 列已经被选取过了. 那么状态转移方程为

$$dp[i][j|k] = Math.min(dp[i][j|k], dp[i - 1][k] + costMatrix[i][j])$$

其中 costMatrix[i][j] 表示第 $i$ 行选取状况为 $j$ 时该行被选取得元素总和.

class Solution {
  public int connectTwoGroups(List<List<Integer>> cost) {
    int m = cost.size(), n = cost.get(0).size();
    int[][] costMatrix = new int[m][1 << n];
    for (int k = 0; k < m; k++) {
      for (int i = 0; i < (1 << n); i++) {
        int sum = 0;
        for (int j = 0; j < n; j++) {
          if ((i & (1 << j)) > 0)
            sum += cost.get(k).get(j);
        }
        costMatrix[k][i] = sum;
      }
    }
    int[][] dp = new int[m][1 << n];
    for (int i = 1; i < m; i++)
      Arrays.fill(dp[i], Integer.MAX_VALUE);
    dp[0] = costMatrix[0];
    for (int i = 1; i < m; i++)
      for (int j = 1; j < (1 << n); j++)
        for (int k = 1; k < (1 << n); k++)
          dp[i][j | k] = Math.min(dp[i][j | k], dp[i - 1][k] + costMatrix[i][j]);
    return dp[m - 1][(1 << n) - 1];
  }
}

最终结果为 dp[m - 1][(1 << n) - 1], 表示选取到 m - 1 行 (即最后一行), 并且每一列都有元素被选取到条件下得元素最小和. 每行都有元素要被选取的约束是由三重循环中 j 和 k 都由 1 开始满足的.

优化

感谢 @Freezer 在评论区里提出用 C++ 会超时的问题, 说明上面的解法效率还没有达到最高. 实际上面解法中的三重循环可以进行优化. 考虑到当我们已知截至上一行时的各列选取情况, 其实并没有必要重复地选取上面已经选取过的列, 据此可以对三重循环做如下修改:

for (int i = 1; i < m; i++) {
  for (int k = 1; k < (1 << n); k++) {
    // 首先将第 i 行只选取一个元素的情况都考虑一遍
    // 这样做的目的是保证第 i 行至少选取了一个元素
    for (int j = 0; j < n; j++)
      dp[i][k | (1 << j)] = Math.min(dp[i][k | (1 << j)], dp[i - 1][k] + cost.get(i).get(j));
    // rest 表示截至第 i 行还没被选过的列
    int rest = (1 << n) - 1 - k;
    // 只遍历没选过的列的所有组合
    for (int j = rest; j  >= 1; j = rest & (j - 1)) {
      dp[i][j | k] = Math.min(dp[i][j | k], dp[i - 1][k] + costMatrix[i][j]);
    }
  }
}

另外注意 dp 中的每一行只依赖上一行的值, 可以将 dp 变为一维数组以优化空间复杂度 (不写了).

统计信息

通过次数	提交次数	AC比率
1949	4155	46.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言