原文链接: https://leetcode-cn.com/problems/maximum-number-of-achievable-transfer-requests

英文原文

We have n buildings numbered from 0 to n - 1. Each building has a number of employees. It's transfer season, and some employees want to change the building they reside in.

You are given an array requests where requests[i] = [fromi, toi] represents an employee's request to transfer from building fromi to building toi.

All buildings are full, so a list of requests is achievable only if for each building, the net change in employee transfers is zero. This means the number of employees leaving is equal to the number of employees moving in. For example if n = 3 and two employees are leaving building 0, one is leaving building 1, and one is leaving building 2, there should be two employees moving to building 0, one employee moving to building 1, and one employee moving to building 2.

Return the maximum number of achievable requests.

 

Example 1:

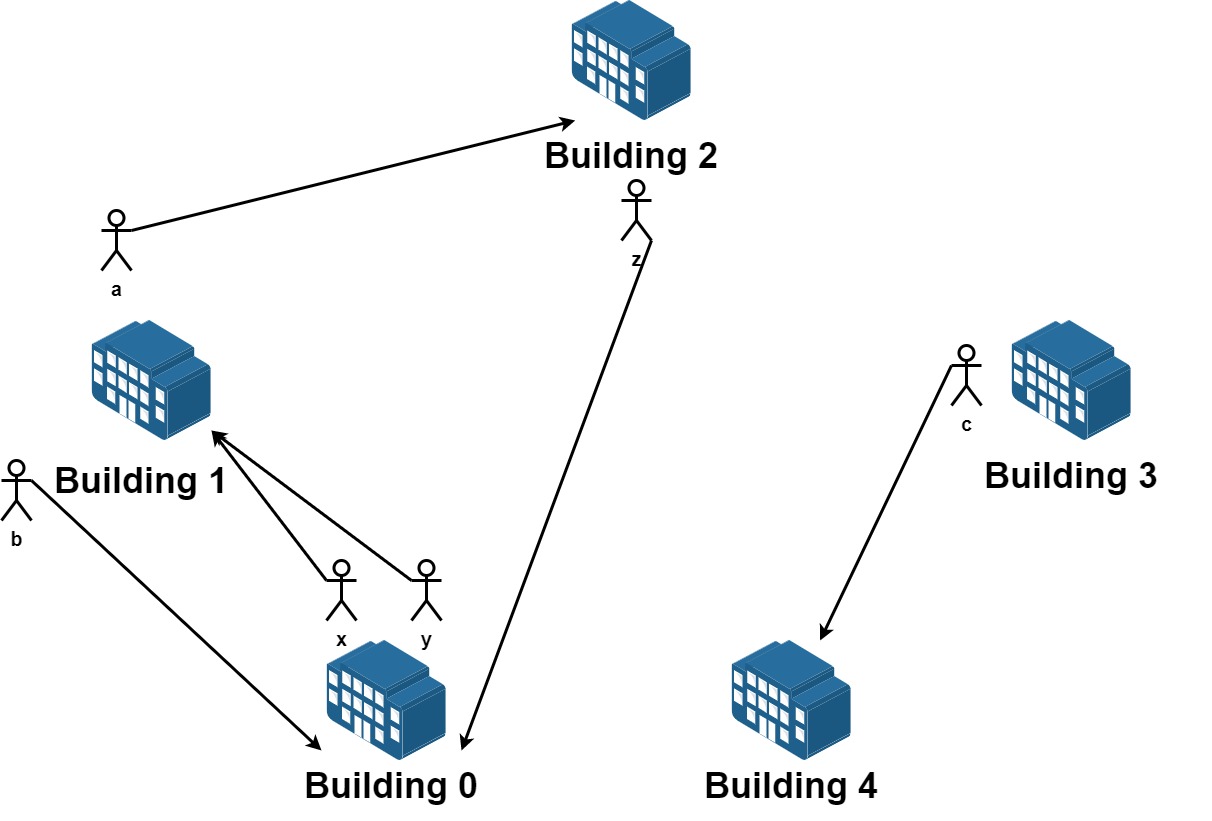
Input: n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
Output: 5
Explantion: Let's see the requests:
From building 0 we have employees x and y and both want to move to building 1.
From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively.
From building 2 we have employee z and they want to move to building 0.
From building 3 we have employee c and they want to move to building 4.
From building 4 we don't have any requests.
We can achieve the requests of users x and b by swapping their places.
We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.

Example 2:

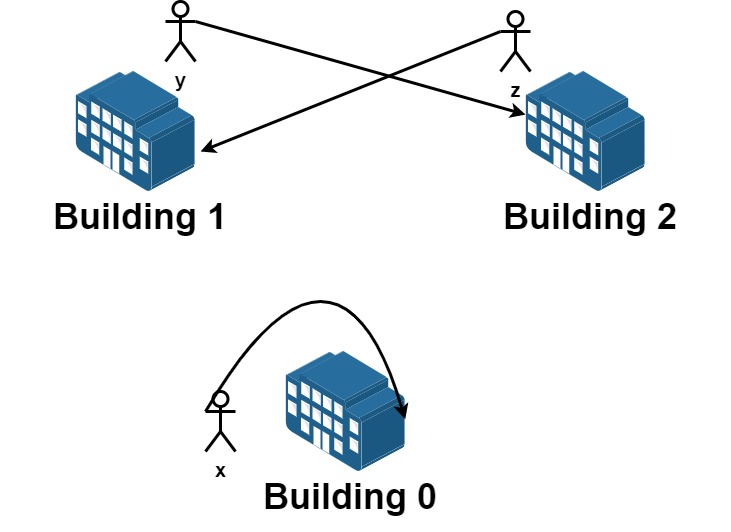
Input: n = 3, requests = [[0,0],[1,2],[2,1]]
Output: 3
Explantion: Let's see the requests:
From building 0 we have employee x and they want to stay in the same building 0.
From building 1 we have employee y and they want to move to building 2.
From building 2 we have employee z and they want to move to building 1.
We can achieve all the requests. 

Example 3:

Input: n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
Output: 4

 

Constraints:

• 1 <= n <= 20
• 1 <= requests.length <= 16
• requests[i].length == 2
• 0 <= fromi, toi < n

中文题目

我们有 n 栋楼，编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节，部分员工想要换一栋楼居住。

给你一个数组 requests ，其中 requests[i] = [fromi, toi] ，表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。

一开始 所有楼都是满的，所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ，一个员工要离开楼 1 ，一个员工要离开楼 2 ，如果该请求列表可行，应该要有两个员工搬入楼 0 ，一个员工搬入楼 1 ，一个员工搬入楼 2 。

请你从原请求列表中选出若干个请求，使得它们是一个可行的请求列表，并返回所有可行列表中最大请求数目。

 

示例 1：

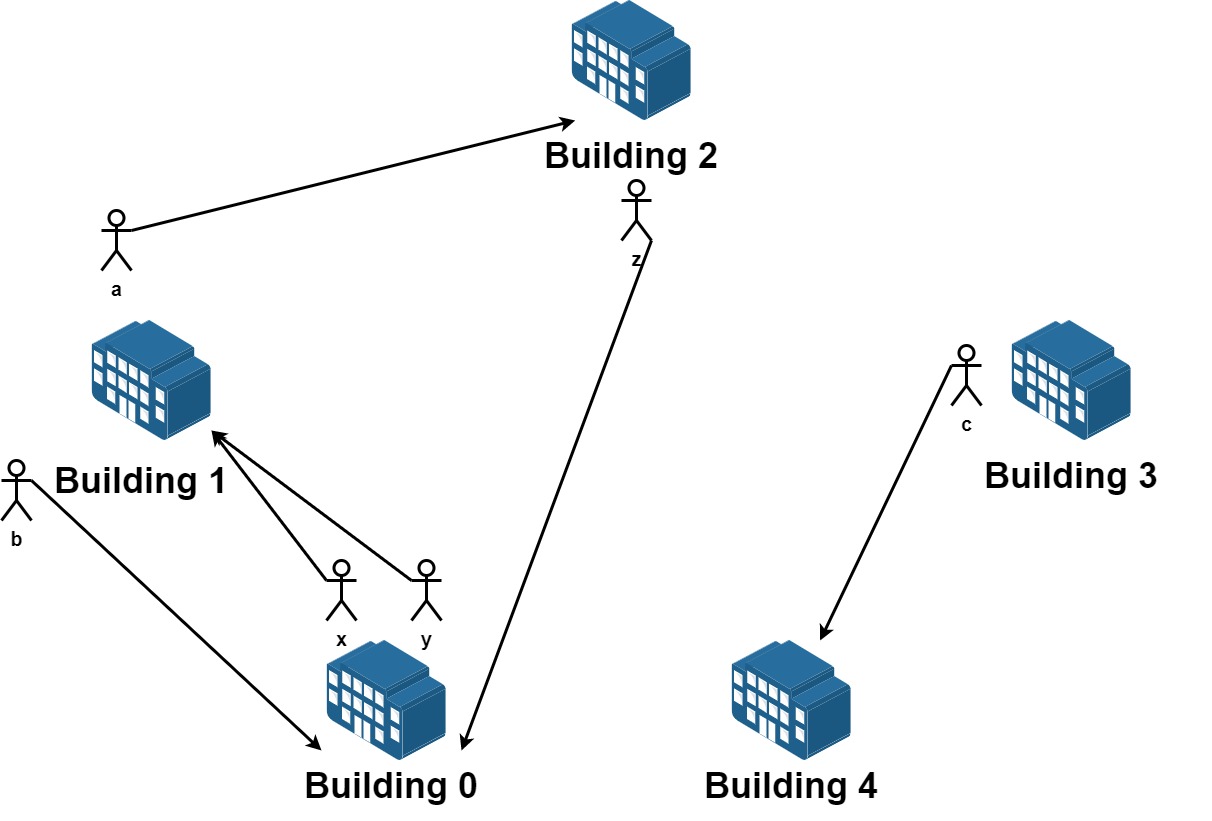
输入：n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出：5
解释：请求列表如下：
从楼 0 离开的员工为 x 和 y ，且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ，且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ，且他想要搬到楼 0 。
从楼 3 离开的员工为 c ，且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼，以满足他们的请求。
我们可以让 y，a 和 z 三人在三栋楼间交换位置，满足他们的要求。
所以最多可以满足 5 个请求。

示例 2：

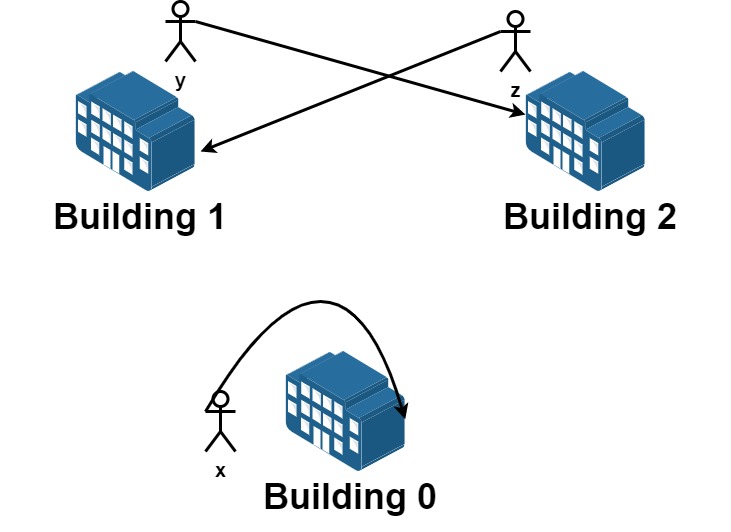
输入：n = 3, requests = [[0,0],[1,2],[2,1]]
输出：3
解释：请求列表如下：
从楼 0 离开的员工为 x ，且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ，且他想要搬到楼 2 。
从楼 2 离开的员工为 z ，且他想要搬到楼 1 。
我们可以满足所有的请求。

示例 3：

输入：n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
输出：4

 

提示：

• 1 <= n <= 20
• 1 <= requests.length <= 16
• requests[i].length == 2
• 0 <= fromi, toi < n

通过代码

高赞题解

考虑将所有边加入答案,此时某些点可能流量不平衡.

对每个点定义$\text{diff}_i=\text{out_degree}_i-\text{in_degree}_i$.
新增源点$S$和汇点$T$.
对每个$\text{diff}_i>0$的点$i$,从$s$向$i$连流量为$\text{diff}_i$费用为0的边.
对每个$\text{diff}_i<0$的点$i$,从$i$向$t$连流量为$-\text{diff}_i$费用为0的边.
原图的边流量和费用为$1$.

新建的图中除$S$和$T$外的点都是流量平衡的.
为了使得原图流量平衡,必须去掉与$S$和$T$相连的边且保持流量平衡,也就是从网络中去掉一个$S$到$T$最大流.
由于代价就是去掉的边数,因此原图的边需要费用$1$.

答案为request.length减去最小费用.

最小费用流的连续最短路算法复杂度为流量*最短路算法复杂度,这里最短路算法可以使用0-1BFS,
因此复杂度为$O(\text{request.length}(\text{request.length} + n))$.

在下面的实现中使用最直接的方法,将每条边拆成流量为$1$后暴力进行边的反向操作.
参考代码:

struct Edge{
    int from, to, cost;
};
class Solution {
public:
    int maximumRequests(int n, vector<vector<int>>& requests) {
        int s = n, t = n + 1, N = n + 2, K = 0;

        //calculate the diff array
        vector<int> diff(n);
        for(auto v : requests){
            diff[v[0]] += 1;
            diff[v[1]] -= 1;
        }

        //create the edges
        vector<Edge> edges;
        for(int i = 0; i < n; i += 1){
            if(diff[i] > 0) for(int j = 0; j < diff[i]; j += 1) edges.push_back({s, i, 0});
            if(diff[i] < 0) for(int j = 0; j < -diff[i]; j += 1) edges.push_back({i, t, 0});
            K += max(diff[i], 0);
        }
        for(auto v : requests) edges.push_back({v[0], v[1], 1});

        //build the graph
        vector<vector<int>> G(N);
        for(int i = 0; i < edges.size(); i += 1){
            G[edges[i].from].push_back(i);
            G[edges[i].to].push_back(i);
        }
        
        int ans = requests.size();
        //using ssp algorithm with 01BFS to find the min-cost max-flow
        vector<int> h(N, 0);
        for(int k = 0; k < K; k += 1){
            vector<int> distance(N, N), pre(N, -1), done(N, 0);
            distance[s] = 0;
            deque<int> q;
            q.push_front(s);
            while(not q.empty()){
                int u = q.front();
                q.pop_front();
                if(done[u]) continue;
                done[u] = 1;
                for(int i : G[u]) if(edges[i].from == u){
                    int w = edges[i].cost + h[u] - h[edges[i].to];
                    if(distance[edges[i].to] > distance[u] + w){
                        distance[edges[i].to] = distance[u] + w;
                        if(w) q.push_back(edges[i].to);
                        else q.push_front(edges[i].to);
                        pre[edges[i].to] = i;
                    }
                }
            }
            for(int i = 0; i < N; i += 1) h[i] += distance[i];
            ans -= h[t];
            for(int u = t; u != s; u = edges[pre[u]].to){
                edges[pre[u]].cost = -edges[pre[u]].cost;
                swap(edges[pre[u]].from, edges[pre[u]].to);
            };
        }
        return ans;
    }
};

统计信息

通过次数	提交次数	AC比率
2241	4570	49.0%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言