原文链接: https://leetcode-cn.com/problems/maximum-number-of-visible-points

英文原文

You are given an array points, an integer angle, and your location, where location = [posx, posy] and points[i] = [xi, yi] both denote integral coordinates on the X-Y plane.

Initially, you are facing directly east from your position. You cannot move from your position, but you can rotate. In other words, posx and posy cannot be changed. Your field of view in degrees is represented by angle, determining how wide you can see from any given view direction. Let d be the amount in degrees that you rotate counterclockwise. Then, your field of view is the inclusive range of angles [d - angle/2, d + angle/2].

You can see some set of points if, for each point, the angle formed by the point, your position, and the immediate east direction from your position is in your field of view.

There can be multiple points at one coordinate. There may be points at your location, and you can always see these points regardless of your rotation. Points do not obstruct your vision to other points.

Return the maximum number of points you can see.

 

Example 1:

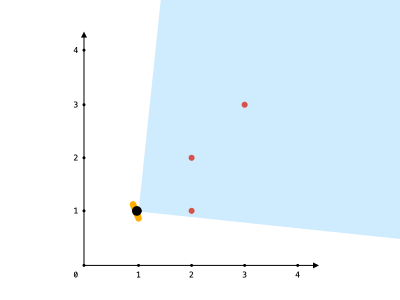
Input: points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
Output: 3
Explanation: The shaded region represents your field of view. All points can be made visible in your field of view, including [3,3] even though [2,2] is in front and in the same line of sight.

Example 2:

Input: points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
Output: 4
Explanation: All points can be made visible in your field of view, including the one at your location.

Example 3:

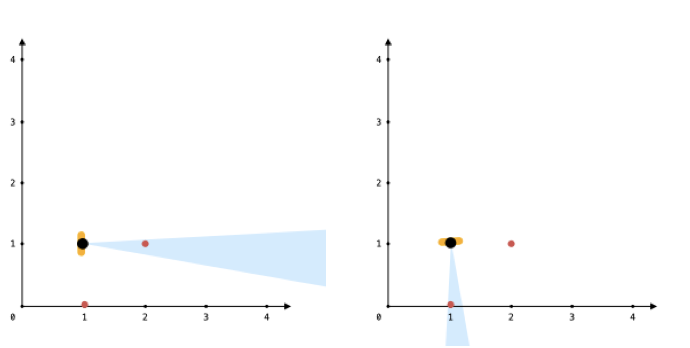
Input: points = [[1,0],[2,1]], angle = 13, location = [1,1]
Output: 1
Explanation: You can only see one of the two points, as shown above.

 

Constraints:

• 1 <= points.length <= 105
• points[i].length == 2
• location.length == 2
• 0 <= angle < 360
• 0 <= posx, posy, xi, yi <= 100

中文题目

给你一个点数组 points 和一个表示角度的整数 angle ，你的位置是 location ，其中 location = [posx, posy] 且 points[i] = [xi, yi] 都表示 X-Y 平面上的整数坐标。

最开始，你面向东方进行观测。你 不能 进行移动改变位置，但可以通过 自转 调整观测角度。换句话说，posx 和 posy 不能改变。你的视野范围的角度用 angle 表示， 这决定了你观测任意方向时可以多宽。设 d 为你逆时针自转旋转的度数，那么你的视野就是角度范围 [d - angle/2, d + angle/2] 所指示的那片区域。

对于每个点，如果由该点、你的位置以及从你的位置直接向东的方向形成的角度 位于你的视野中 ，那么你就可以看到它。

同一个坐标上可以有多个点。你所在的位置也可能存在一些点，但不管你的怎么旋转，总是可以看到这些点。同时，点不会阻碍你看到其他点。

返回你能看到的点的最大数目。

 

示例 1：

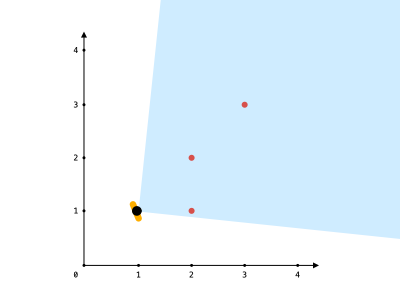
输入：points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
输出：3
解释：阴影区域代表你的视野。在你的视野中，所有的点都清晰可见，尽管 [2,2] 和 [3,3]在同一条直线上，你仍然可以看到 [3,3] 。

示例 2：

输入：points = [[2,1],[2,2],[3,4],[1,1]], angle = 90, location = [1,1]
输出：4
解释：在你的视野中，所有的点都清晰可见，包括你所在位置的那个点。

示例 3：

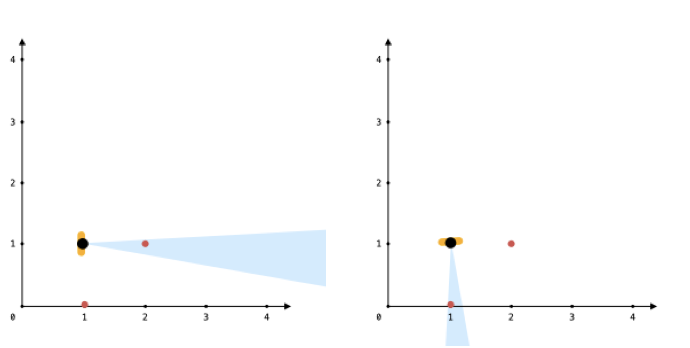
输入：points = [[1,0],[2,1]], angle = 13, location = [1,1]
输出：1
解释：如图所示，你只能看到两点之一。

 

提示：

• 1 <= points.length <= 105
• points[i].length == 2
• location.length == 2
• 0 <= angle < 360
• 0 <= posx, posy, xi, yi <= 100

通过代码

高赞题解

本场周赛题解 | 我的LeetCode比赛题解

首先排除与人的位置重合的点，只考虑剩下的点。

计算每个点到人的位置的极角，然后按极角排序。因为可以循环，所以把整个数组加上$360^\circ$再接到后面。

接下来双指针找出覆盖最多点的区间即可。

最后返回答案时，把与人的位置重合的点加上。

总时间复杂度$O(N\log N)$。

更新：角度计算用atan2更加方便，不需要判断象限。

const double eps = 1e-8;

class Solution {
public:
    int visiblePoints(vector<vector<int>>& points, int angle, vector<int>& location) {
        int x = location[0], y = location[1];
        int same = 0;
        vector<double> v;
        for (auto p : points) {
            int px = p[0], py = p[1];
            if (px == x && py == y)
                same++;
            else
                v.emplace_back(atan2(py - y, px - x) * 180 / M_PI);
        }
        sort(v.begin(), v.end());
        int m = v.size();
        for (int i = 0; i < m; ++i)
            v.emplace_back(v[i] + 360);
        int r = 0, hi = 0;
        for (int l = 0; l < m; ++l) {
            while (r + 1 < v.size() && v[r + 1] - v[l] <= (double)angle + eps)
                r++;
            hi = max(hi, r - l + 1);
        }
        return hi + same;
    }
};

统计信息

通过次数	提交次数	AC比率
2465	9008	27.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言