1617-统计子树中城市之间最大距离(Count Subtrees With Max Distance Between Cities)

原文链接: https://leetcode-cn.com/problems/count-subtrees-with-max-distance-between-cities

英文原文

There are n cities numbered from 1 to n. You are given an array edges of size n-1, where edges[i] = [u_i, v_i] represents a bidirectional edge between cities u_i and v_i. There exists a unique path between each pair of cities. In other words, the cities form a tree.

A subtree is a subset of cities where every city is reachable from every other city in the subset, where the path between each pair passes through only the cities from the subset. Two subtrees are different if there is a city in one subtree that is not present in the other.

For each d from 1 to n-1, find the number of subtrees in which the maximum distance between any two cities in the subtree is equal to d.

Return an array of size n-1 where the d^th element (1-indexed) is the number of subtrees in which the maximum distance between any two cities is equal to d.

Notice that the distance between the two cities is the number of edges in the path between them.

Example 1:

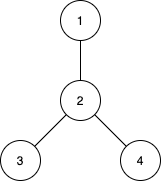
Input: n = 4, edges = [[1,2],[2,3],[2,4]]
Output: [3,4,0]
Explanation:
The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
No subtree has two nodes where the max distance between them is 3.

Example 2:

Input: n = 2, edges = [[1,2]]
Output: [1]

Example 3:

Input: n = 3, edges = [[1,2],[2,3]]
Output: [2,1]

Constraints:

2 <= n <= 15
edges.length == n-1
edges[i].length == 2
1 <= u_i, v_i <= n
All pairs (u_i, v_i) are distinct.

中文题目

给你 n 个城市，编号为从 1 到 n 。同时给你一个大小为 n-1 的数组 edges ，其中 edges[i] = [u_i, v_i] 表示城市 u_i 和 v_i之间有一条双向边。题目保证任意城市之间只有唯一的一条路径。换句话说，所有城市形成了一棵树。

一棵子树是城市的一个子集，且子集中任意城市之间可以通过子集中的其他城市和边到达。两个子树被认为不一样的条件是至少有一个城市在其中一棵子树中存在，但在另一棵子树中不存在。

对于 d 从 1 到 n-1 ，请你找到城市间 最大距离 恰好为 d 的所有子树数目。

请你返回一个大小为 n-1 的数组，其中第 d 个元素（下标从 1 开始）是城市间 最大距离 恰好等于 d 的子树数目。

请注意，两个城市间距离定义为它们之间需要经过的边的数目。

示例 1：

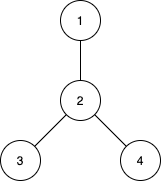
输入：n = 4, edges = [[1,2],[2,3],[2,4]]
输出：[3,4,0]
解释：
子树 {1,2}, {2,3} 和 {2,4} 最大距离都是 1 。
子树 {1,2,3}, {1,2,4}, {2,3,4} 和 {1,2,3,4} 最大距离都为 2 。
不存在城市间最大距离为 3 的子树。

示例 2：

输入：n = 2, edges = [[1,2]]
输出：[1]

示例 3：

输入：n = 3, edges = [[1,2],[2,3]]
输出：[2,1]

提示：

2 <= n <= 15
edges.length == n-1
edges[i].length == 2
1 <= u_i, v_i <= n
题目保证 (u_i, v_i) 所表示的边互不相同。

通过代码

高赞题解

看到这道题目的时候我最头痛的是，怎么不重不漏地统计子树？

想要不重，很简单，题目已经给出暗示了2 <= n <= 15，闭着眼睛都知道要用状压。

那么不漏怎么办？
我的想法还是，对每一个j（j表示成二进制，从右数第k位为1表示第k个节点在子树中否则不在），逐一检查i=1, 2, ..., n是不是这个子树的邻接边–如果是邻接边，那么这个子树中必然存在一个节点k，使得dist[i][k]=1。此时，只用对目前加进来的这个点i和子树中的每一个节点求距离最大值即可。

从上述过程中，我们发现会常常用到两点距离。由于节点数量并不多2 <= n <= 15，n^3也不是什么可怕的计算量，所以干脆用Floyed把所有两点之间的距离全部算出来。

以下代码我进行了详细注释。如果还看不懂可以在评论区留言。

class Solution {
    public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
        int[][] dist=new int[n][n]; //存储两点之间的距离
        for(int i=0; i<n; i++){
            Arrays.fill(dist[i], Integer.MAX_VALUE);
            //之后要求最小值 所以初始化成最大整数
            //其实初始化成任何一个大于等于n的数字都可以
            dist[i][i]=0;//本身到本身显然为0
        }        
        int[] dp=new int[1<<(n)];
        //状态压缩存储 dp[j]表示子树j的最大距离
        //j表示成二进制，从右数第k位为1表示第k个节点在子集中否则不在
        for(int[] edge:edges){
            // 直接相连的两点之间距离显然为1
            dist[edge[0]-1][edge[1]-1]=1;
            dist[edge[1]-1][edge[0]-1]=1;
            // 直接相连的两点可以构成一棵子树 它们的最大距离为1
            dp[(1<<(edge[0]-1)) + (1<<(edge[1]-1))]=1;
        }
        // Floyed算法 求每两点之间的最短距离 请全文背诵
        for(int k=0; k<n; k++){
            for(int i=0; i<n; i++){
                for(int j=0; j<n; j++){
                    if(dist[i][k]!=Integer.MAX_VALUE && dist[k][j]!=Integer.MAX_VALUE){
                        dist[i][j]=Math.min(dist[i][j], dist[i][k]+dist[k][j]);
                    }
                }
            }
        }
        // 把对j的循环放在外面
        // 因为显然如果子树A是子树B的一部分 jA<jB
        // 所以要把数字小的j全部求好了再去求数字大的j
        for(int j=1; j<dp.length; j++){
            // 以下我们从子树 j 扩展到子树 j+(1<<i)
            // 即把节点i加入到子树j中
            // 如果本身j就无法构成一棵子树（如果j表示的节点不能相互连通）
            // 那么也就没有必要继续了 所以continue
            if(dp[j]==0) continue;
            for(int i=0; i<n; i++){
                // 如果节点i已经在子树j中 或者 j+(1<<i)已经被计算过了 就没必要算了
                // 为什么它可能会已经被计算过呢？ 
                // 因为 111=101+10=11+100 添加点的顺序不同 但是能得出同样的一棵子树
                if(((1<<i)&j)!=0 || dp[j+(1<<i)]!=0) continue;
                // 检查 j 子树中是否有和 i 直接相连的点 
                // 这其实是相对于子树（而不是某个节点的）的bfs
                for(int k=0; k<n; k++){
                    if(((1<<k)&j)!=0 && dist[i][k]==1){
                        dp[j+(1<<i)]=dp[j];
                        break;
                    }
                }
                // 如果j 子树中没有和 i 直接相连的点
                // 那么也就无法添加这个节点i了
                if(dp[j+(1<<i)]==0) continue;
                // 把节点i添加进来 就要更新新子树的最大距离 dp[j+(1<<i)]
                // 更新的办法是 对于原子树的每一个节点和新节点求最大距离
                // 因为只产生了这些新距离 做增量计算就好
                for(int kk=0; kk<n; kk++){
                    if(((1<<kk)&j)!=0){
                        dp[j+(1<<i)]=Math.max(dp[j+(1<<i)], dist[i][kk]);
                    }
                }
            }
        }
        // 统计结果 由于下标从1开始 
        // ans[0]其实记录的是最大距离为1的子树有多少棵 统计时要-1
        int[] ans=new int[n-1];
        for(int j=0; j<dp.length; j++){
            if(dp[j]!=0) ans[dp[j]-1]++;
        }
        return ans;
    }
}

上述代码是从子树 j 扩展到子树 j+(1<<i)
如果从子树 j-(1<<i) 扩展到子树 j 也是可以的–实际上这才是状压状态转移方程时常用的做法。
我刚刚改了一下就得到了这一种，但速度要慢很多。（我猜是这个判断语句多了移位的操作？ ((1<<k)&j-(1<<i))）

class Solution {
    public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
        int[][] dist=new int[n][n];
        for(int i=0; i<n; i++){
            Arrays.fill(dist[i], Integer.MAX_VALUE);
            dist[i][i]=0;
        }        
        int[] dp=new int[1<<(n)];
        for(int[] edge:edges){
            dist[edge[0]-1][edge[1]-1]=1;
            dist[edge[1]-1][edge[0]-1]=1;
            dp[(1<<(edge[0]-1)) + (1<<(edge[1]-1))]=1;
        }
        for(int k=0; k<n; k++){
            for(int i=0; i<n; i++){
                for(int j=0; j<n; j++){
                    if(dist[i][k]!=Integer.MAX_VALUE && dist[k][j]!=Integer.MAX_VALUE){
                        dist[i][j]=Math.min(dist[i][j], dist[i][k]+dist[k][j]);
                    }
                }
            }
        }
        for(int j=1; j<dp.length; j++){
            for(int i=0; i<n; i++){
                if(((1<<i)&j)==0) continue;
                if(dp[j-(1<<i)]!=0){
                    for(int k=0; k<n; k++){
                        if(((1<<k)&j-(1<<i))!=0 && dist[i][k]==1){
                            dp[j]=dp[j-(1<<i)];
                            break;
                        }
                    }
                    if(dp[j]==0) continue;
                    for(int k=0; k<n; k++){
                        if(((1<<k)&j)!=0){
                            dp[j]=Math.max(dp[j], dist[i][k]);
                        }
                    }
                }
                if(dp[j]!=0) break;
            }
        }
        int[] ans=new int[n-1];
        for(int j=0; j<dp.length; j++){
            if(dp[j]!=0) ans[dp[j]-1]++;
        }
        return ans;
    }
}

最后，我的GitHub leetcode题解已收录题解200+，欢迎关注。

统计信息

通过次数	提交次数	AC比率
1807	2900	62.3%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途