1632-矩阵转换后的秩(Rank Transform of a Matrix)
发表于：2021-12-03 | 分类： 困难
字数统计: 1.3k | 阅读时长: 7分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/rank-transform-of-a-matrix

英文原文

Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].

The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:

  • The rank is an integer starting from 1.
  • If two elements p and q are in the same row or column, then:
    • If p < q then rank(p) < rank(q)
    • If p == q then rank(p) == rank(q)
    • If p > q then rank(p) > rank(q)
  • The rank should be as small as possible.

It is guaranteed that answer is unique under the given rules.

 

Example 1:

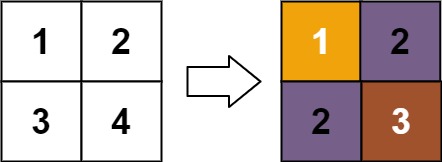
Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.

Example 2:

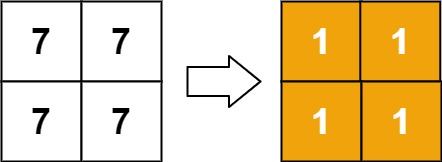
Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]

Example 3:

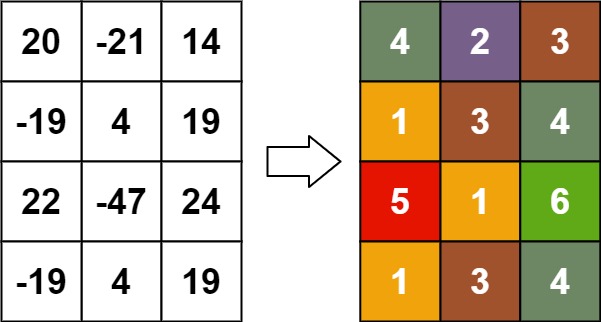
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

Example 4:

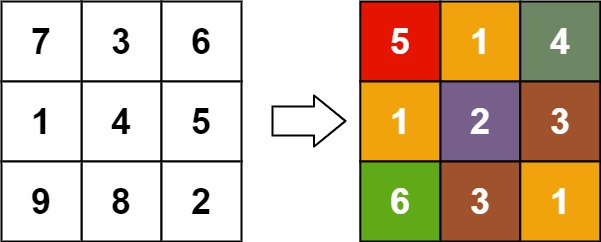
Input: matrix = [[7,3,6],[1,4,5],[9,8,2]]
Output: [[5,1,4],[1,2,3],[6,3,1]]

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 500
  • -109 <= matrix[row][col] <= 109

中文题目

给你一个 m x n 的矩阵 matrix ，请你返回一个新的矩阵 answer ，其中 answer[row][col] 是 matrix[row][col] 的秩。

每个元素的 秩 是一个整数，表示这个元素相对于其他元素的大小关系，它按照如下规则计算：

  • 秩是从 1 开始的一个整数。
  • 如果两个元素 p 和 q 在 同一行 或者 同一列 ，那么：
    • 如果 p < q ，那么 rank(p) < rank(q)
    • 如果 p == q ，那么 rank(p) == rank(q)
    • 如果 p > q ，那么 rank(p) > rank(q)
  • 秩 需要越 小 越好。

题目保证按照上面规则 answer 数组是唯一的。

 

示例 1：

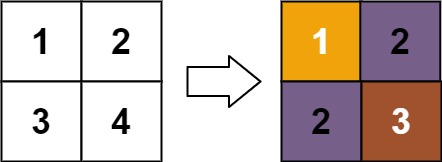
输入：matrix = [[1,2],[3,4]]
输出：[[1,2],[2,3]]
解释：
matrix[0][0] 的秩为 1 ，因为它是所在行和列的最小整数。
matrix[0][1] 的秩为 2 ，因为 matrix[0][1] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][0] 的秩为 2 ，因为 matrix[1][0] > matrix[0][0] 且 matrix[0][0] 的秩为 1 。
matrix[1][1] 的秩为 3 ，因为 matrix[1][1] > matrix[0][1]， matrix[1][1] > matrix[1][0] 且 matrix[0][1] 和 matrix[1][0] 的秩都为 2 。

示例 2：

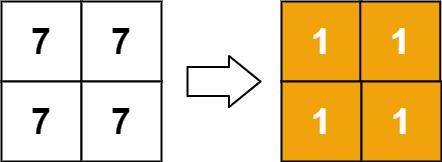
输入：matrix = [[7,7],[7,7]]
输出：[[1,1],[1,1]]

示例 3：

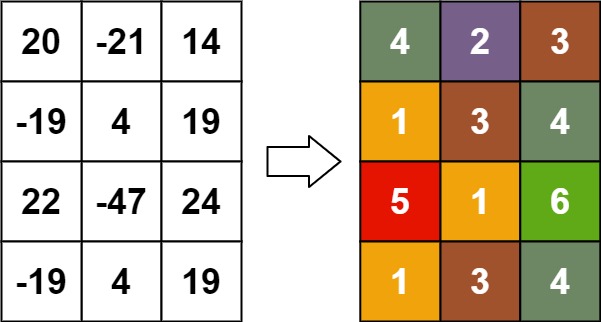
输入：matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
输出：[[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

示例 4：

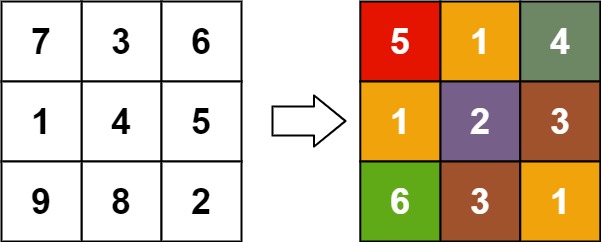
输入：matrix = [[7,3,6],[1,4,5],[9,8,2]]
输出：[[5,1,4],[1,2,3],[6,3,1]]

 

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 500
  • -109 <= matrix[row][col] <= 109

通过代码

高赞题解

题目分析

首先，将每行及每列中相等的元素找出来，然后连并查集的边，注意这里不需要连所有边，只要相邻两个连边即可。在后面的过程中，我们只考虑并查集中每一个连通分量的根节点。

接下来，每行每列分别排序，根据排序后的大小关系连拓扑排序的边。同样，这里也不需要连所有边，只要相邻两个大小不等的元素连边即可。

然后，进行拓扑排序。每个点的秩初始都为$1$，在拓扑排序过程中，如果有一条 $u\to v$ 的边，则将 $v$ 的秩设置为 $\max(rank(v), rank(u)+1)$。其余操作同一般的拓扑排序。

最后，将矩阵中每个点的秩设置为并查集中其所在的连通分量的根节点的秩即可。

复杂度

  • 时间复杂度 $O(NM\log\max(N,M))$，瓶颈为排序。

参考代码（C++）

class UnionFind {
  int n;
  vector<int> parent, size;

public:
  UnionFind(int n) {
    this->n = n;
    parent = vector<int>(n);
    size = vector<int>(n, 1);
    for (int i = 0; i < n; ++i)
      parent[i] = i;
  }

  int find(int idx) {
    if (parent[idx] == idx)
      return idx;
    return parent[idx] = find(parent[idx]);
  }

  void connect(int a, int b) {
    int fa = find(a), fb = find(b);
    if (fa != fb) {
      if (size[fa] > size[fb]) {
        parent[fb] = fa;
        size[fa] += size[fb];
      } else {
        parent[fa] = fb;
        size[fb] += size[fa];
      }
    }
  }
};

class Solution {
public:
    vector<vector<int>> matrixRankTransform(vector<vector<int>>& matrix) {
        int n = matrix.size(), m = matrix[0].size();
        UnionFind uf(n * m);
        for (int i = 0; i < n; ++i) {
            map<int, vector<int>> mp;
            for (int j = 0; j < m; ++j)
                mp[matrix[i][j]].emplace_back(i * m + j);
            for (auto &[num, vec] : mp) {
                for (int k = 0; k + 1 < vec.size(); ++k)
                    uf.connect(vec[k], vec[k + 1]);
            }
        }
        for (int j = 0; j < m; ++j) {
            map<int, vector<int>> mp;
            for (int i = 0; i < n; ++i)
                mp[matrix[i][j]].emplace_back(i * m + j);
            for (auto &[num, vec] : mp) {
                for (int k = 0; k + 1 < vec.size(); ++k)
                    uf.connect(vec[k], vec[k + 1]);
            }
        }
        vector<vector<int>> adj(n * m);
        vector<int> indegree(n * m);
        for (int i = 0; i < n; ++i) {
            vector<pair<int, int>> v(m);
            for (int j = 0; j < m; ++j)
                v[j] = make_pair(matrix[i][j], j);
            sort(v.begin(), v.end());
            for (int j = 0; j + 1 < m; ++j)
                if (v[j].first != v[j + 1].first) {
                    int uu = uf.find(i * m + v[j].second);
                    int vv = uf.find(i * m + v[j + 1].second);
                    adj[uu].emplace_back(vv);
                    indegree[vv]++;
                }
        }
        for (int j = 0; j < m; ++j) {
            vector<pair<int, int>> v(n);
            for (int i = 0; i < n; ++i)
                v[i] = make_pair(matrix[i][j], i);
            sort(v.begin(), v.end());
            for (int i = 0; i + 1 < n; ++i)
                if (v[i].first != v[i + 1].first) {
                    int uu = uf.find(v[i].second * m + j);
                    int vv = uf.find(v[i + 1].second * m + j);
                    adj[uu].emplace_back(vv);
                    indegree[vv]++;
                }
        }
        vector<int> ans(n * m, 1);
        queue<int> q;
        for (int i = 0; i < n * m; ++i) {
            if (uf.find(i) == i && indegree[i] == 0)
                q.emplace(i);
        }
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            for (int v : adj[u]) {
                ans[v] = max(ans[v], ans[u] + 1);
                indegree[v]--;
                if (indegree[v] == 0)
                    q.emplace(v);
            }
        }
        vector<vector<int>> result(n, vector<int>(m));
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < m; ++j)
                result[i][j] = ans[uf.find(i * m + j)];
        return result;
    }
};

持续更新更多优质题解，欢迎 🌟关注我

统计信息

通过次数 提交次数 AC比率
1518 4723 32.1%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
数组 矩阵 贪心 图 拓扑排序 并查集
上一篇:
1331-数组序号转换(Rank Transform of an Array)
下一篇:
1146-快照数组(Snapshot Array)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo