1691-堆叠长方体的最大高度(Maximum Height by Stacking Cuboids )

原文链接: https://leetcode-cn.com/problems/maximum-height-by-stacking-cuboids

英文原文

Given n cuboids where the dimensions of the i^th cuboid is cuboids[i] = [width_i, length_i, height_i] (0-indexed). Choose a subset of cuboids and place them on each other.

You can place cuboid i on cuboid j if width_i <= width_j and length_i <= length_j and height_i <= height_j. You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid.

Return the maximum height of the stacked cuboids.

Example 1:

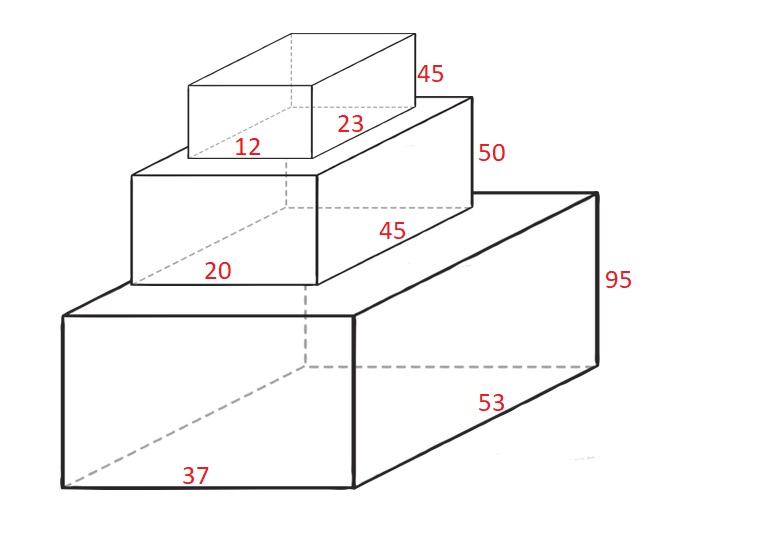
Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]]
Output: 190
Explanation:
Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95.
Cuboid 0 is placed next with the 45x20 side facing down with height 50.
Cuboid 2 is placed next with the 23x12 side facing down with height 45.
The total height is 95 + 50 + 45 = 190.

Example 2:

Input: cuboids = [[38,25,45],[76,35,3]]
Output: 76
Explanation:
You can't place any of the cuboids on the other.
We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.

Example 3:

Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
Output: 102
Explanation:
After rearranging the cuboids, you can see that all cuboids have the same dimension.
You can place the 11x7 side down on all cuboids so their heights are 17.
The maximum height of stacked cuboids is 6 * 17 = 102.

Constraints:

n == cuboids.length
1 <= n <= 100
1 <= width_i, length_i, height_i <= 100

中文题目

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [width_i, length_i, height_i]（下标从 0 开始）。请你从 cuboids 选出一个子集，并将它们堆叠起来。

如果 width_i <= width_j 且 length_i <= length_j 且 height_i <= height_j ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。

返回 堆叠长方体 cuboids 可以得到的 最大高度 。

示例 1：

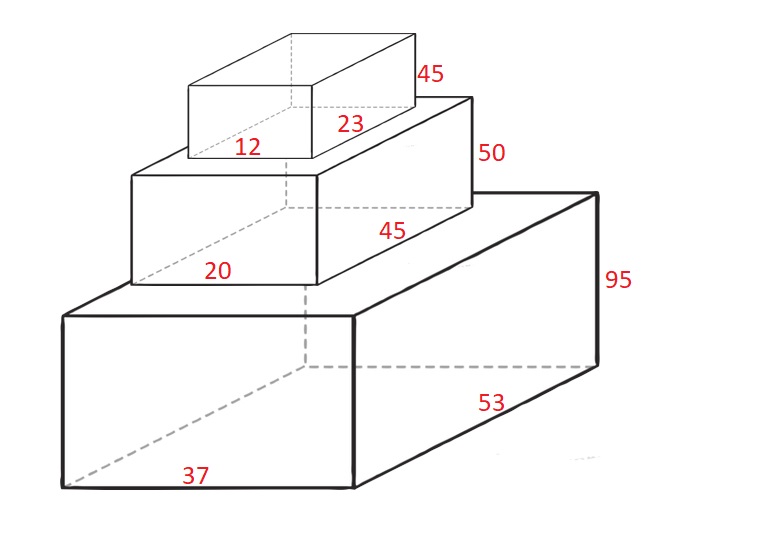
输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
输出：190
解释：
第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。

示例 2：

输入：cuboids = [[38,25,45],[76,35,3]]
输出：76
解释：
无法将任何长方体放在另一个上面。
选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。

示例 3：

输入：cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
输出：102
解释：
重新排列长方体后，可以看到所有长方体的尺寸都相同。
你可以把 11x7 的一面朝下，这样它们的高度就是 17 。
堆叠长方体的最大高度为 6 * 17 = 102 。

提示：

n == cuboids.length
1 <= n <= 100
1 <= width_i, length_i, height_i <= 100

通过代码

高赞题解

方法一：动态规划 + 自定义排序

思路与算法

由于我们要最大化的是「高度」，因此很容易想到将每个长方体的最长边做为高度是最优的。但这样做真的是对的吗？

我们可以尝试证明这一点，credit to @han3000：

对于任意一种堆叠方法，假设长方体的数目为 $k$，这些长方体分别为 $(w_1, l_1, h_1), \cdots, (w_n, l_n, h_n)$，如果将每一个长方体内部的三条边按照从小到大的顺序重新排列，记为 $(w_i, l_i, h_i) \to (w_i’, l_i’, h_i’)$，其中 $w_i’, l_i’, h_i’$ 分别是三者中的最小值、中间值、最大值，那么得到的 $(w_1’, l_1’, h_1’), \cdots, (w_n’, l_n’, h_n’)$ 仍然是满足堆叠要求的。

证明略。对于任意的 $j < i$，枚举一下所有 $(w_j, l_j, h_j, w_i, l_i, h_i)$ 的相对顺序即可。

当所有长方体内部的三条边按照从小到大的顺序重新排列之后，由于此时高度对应了最大值，那么整个堆叠的高度之和一定不会比重新排列以前要矮，因此最优的堆叠方法一定是基于重新排列的。

那么我们怎么计算这个堆叠高度呢？我们可以使用动态规划并写出状态转移方程：

$$
f(i) = \max_{w_j’\leq w_i’, l_j’\leq l_i’, h_j’\leq h_i’} \big{ f(j) \big} + h_i
$$

其中 $f(i)$ 表示以 $(w_i’, l_i’, h_i’)$ 为最后一个长方体的最大高度。我们需要找到某个索引 $j$ 作为倒数第二个长方体，并且它可以放在第 $i$ 个长方体上。特别地，如果不存在这样的索引 $j$，那么我们可以只放第 $i$ 个长方体就行了，状态转移方程简化为 $f(i) = h_i’$。最终的答案即为 $\max f$。

要想实现上面这个动态规划，我们需要保证当枚举到第 $i$ 个长方体时，所有可以堆叠在第 $i$ 个长方体之上的长方体都应该枚举过，因此在动态规划之前，我们还需要将所有的长方体按照 $(w_i’, l_i’, h_i’)$ 三个关键字进行升序排序。其实这里有非常多的排序方法，只要保证枚举关系的拓扑性即可，例如我们可以仅使用两个关键字 $(h_i’, w_i’+l_i’)$ 进行排序也能达到同样的效果。

代码

[sol1-C++]
class Solution {
public:
    int maxHeight(vector<vector<int>>& cuboids) {
        int n = cuboids.size();
        for (auto& cubic: cuboids) {
            sort(cubic.begin(), cubic.end());
        }
        
        // 保证枚举关系拓扑性的排序都可以
        // sort(cuboids.begin(), cuboids.end());
        sort(cuboids.begin(), cuboids.end(), [](const auto& u, const auto& v) {
            return pair(u[2], u[0] + u[1]) < pair(v[2], v[0] + v[1]);
        });
        
        vector<int> f(n);
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                if (cuboids[j][0] <= cuboids[i][0] && cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2]) {
                    f[i] = max(f[i], f[j]);
                }
            }
            f[i] += cuboids[i][2];
        }
        
        return *max_element(f.begin(), f.end());
    }
};

复杂度分析

时间复杂度：$O(n^2)$。
空间复杂度：$O(n)$。

方法二：懒得思考的动态规划

思路与算法

其实我们也可以放弃思考，把每一个 $(w_i, l_i, h_i)$ 的六种排列情况全部放在一个数组中进行排序，然后再动态规划。由于本题 $n\leq 100$ 因此这样的方法是可以通过的，但如果 $n \leq 1000$ 或者 $2000$ 那么就只有方法一可以通过了。

代码

[sol2-C++]
class Solution {
public:
    int maxHeight(vector<vector<int>>& cuboids) {
        int n = cuboids.size();
        vector<tuple<int, int, int, int>> v;
        for (int i = 0; i < n; ++i) {
            const auto& cubic = cuboids[i];
            v.emplace_back(cubic[0], cubic[1], cubic[2], i);
            v.emplace_back(cubic[0], cubic[2], cubic[1], i);
            v.emplace_back(cubic[1], cubic[0], cubic[2], i);
            v.emplace_back(cubic[1], cubic[2], cubic[0], i);
            v.emplace_back(cubic[2], cubic[0], cubic[1], i);
            v.emplace_back(cubic[2], cubic[1], cubic[0], i);
        }
        
        sort(v.begin(), v.end());
        
        vector<int> f(n * 6);
        for (int i = 0; i < n * 6; ++i) {
            auto [wi, li, hi, idi] = v[i];
            for (int j = 0; j < i; ++j) {
                auto [wj, lj, hj, idj] = v[j];
                if (wj <= wi && lj <= li && hj <= hi && idj != idi) {
                    f[i] = max(f[i], f[j]);
                }
            }
            f[i] += hi;
        }
        
        return *max_element(f.begin(), f.end());
    }
};

复杂度分析

时间复杂度：$O(n^2)$。
空间复杂度：$O(n)$。

统计信息

通过次数	提交次数	AC比率
2522	5138	49.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途