1857-有向图中最大颜色值(Largest Color Value in a Directed Graph)

原文链接: https://leetcode-cn.com/problems/largest-color-value-in-a-directed-graph

英文原文

There is a directed graph of n colored nodes and m edges. The nodes are numbered from 0 to n - 1.

You are given a string colors where colors[i] is a lowercase English letter representing the color of the i^th node in this graph (0-indexed). You are also given a 2D array edges where edges[j] = [a_j, b_j] indicates that there is a directed edge from node a_j to node b_j.

A valid path in the graph is a sequence of nodes x₁ -> x₂ -> x₃ -> ... -> x_k such that there is a directed edge from x_i to x_i+1 for every 1 <= i < k. The color value of the path is the number of nodes that are colored the most frequently occurring color along that path.

Return the largest color value of any valid path in the given graph, or -1 if the graph contains a cycle.

Example 1:

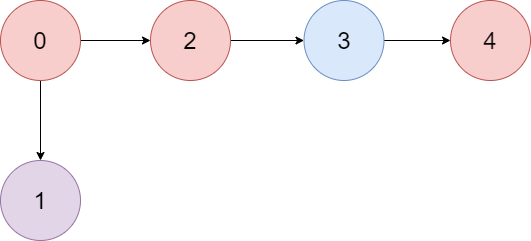
Input: colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
Output: 3
Explanation: The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored "a" (red in the above image).

Example 2:

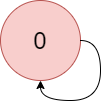
Input: colors = "a", edges = [[0,0]]
Output: -1
Explanation: There is a cycle from 0 to 0.

Constraints:

n == colors.length
m == edges.length
1 <= n <= 10⁵
0 <= m <= 10⁵
colors consists of lowercase English letters.
0 <= a_j, b_j < n

中文题目

给你一个 有向图 ，它含有 n 个节点和 m 条边。节点编号从 0 到 n - 1 。

给你一个字符串 colors ，其中 colors[i] 是小写英文字母，表示图中第 i 个节点的颜色（下标从 0 开始）。同时给你一个二维数组 edges ，其中 edges[j] = [a_j, b_j] 表示从节点 a_j 到节点 b_j有一条 有向边 。

图中一条有效路径是一个点序列 x₁ -> x₂ -> x₃ -> ... -> x_k ，对于所有 1 <= i < k ，从 x_i 到 x_i+1 在图中有一条有向边。路径的 颜色值 是路径中 出现次数最多 颜色的节点数目。

请你返回给定图中有效路径里面的 最大颜色值 。如果图中含有环，请返回 -1 。

示例 1：

输入：colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
输出：3
解释：路径 0 -> 2 -> 3 -> 4 含有 3 个颜色为 "a" 的节点（上图中的红色节点）。

示例 2：

输入：colors = "a", edges = [[0,0]]
输出：-1
解释：从 0 到 0 有一个环。

提示：

n == colors.length
m == edges.length
1 <= n <= 10⁵
0 <= m <= 10⁵
colors 只含有小写英文字母。
0 <= a_j, b_j < n

通过代码

高赞题解

方法一：拓扑排序 + 动态规划

提示 $1$

我们需要求出的答案等价于：

对于一种颜色 $c$，以及一条路径 $\textit{path}$，其中颜色为 $c$ 的节点有 $\textit{path}_c$ 个。我们希望挑选 $c$ 以及 $\textit{path}$，使得 $\textit{path}_c$ 的值最大。

提示 $2$

根据提示 $1$，我们可以枚举颜色 $c$，随后选出可以使得 $\textit{path}_c$ 达到最大值的 $\textit{path}$。这些 $\textit{path}_c$ 中的最大值即为答案。

提示 $3$

如果给定的有向图包含环，那么它不存在拓扑排序。

如果给定的有向图不包含环，那么这个有向图是一个「有向无环图」，它一定存在拓扑排序。

根据拓扑排序的性质，如果节点 $a$ 有一条有向边指向节点 $b$，那么 $b$ 在拓扑排序中一定出现在 $a$ 之后。因此，一条路径上点的顺序与它们在拓扑排序中出现的顺序是一致的。

提示 $4$

我们可以根据拓扑排序来进行动态规划。

设 $f(v, c)$ 表示以节点 $v$ 为终点的所有路径中，包含颜色 $c$ 的节点数量的最大值。在进行状态转移时，我们考虑所有 $v$ 的前驱节点（即有一条有向边指向 $v$ 的节点）$\textit{prev}_v$：

$$
f(v, c) = \left( \max_{u \in \textit{prev}_j} f(u, c) \right) + \mathbb{I}(v, c)
$$

即找出前驱节点中包含颜色 $c$ 的节点数量最多的那个节点进行转移，并且如果 $v$ 本身的颜色为 $c$，$f(v, c)$ 的值就增加 $1$。这里 $\mathbb{I}(v, c)$ 为示性函数，当节点 $v$ 的颜色为 $c$ 时，函数值为 $1$，否则为 $0$。

那么 $\textit{path}_c$ 的值即为 $f(v, c)$ 中的最大值。

思路与算法

我们可以将状态转移融入使用广度优先搜索的方法求解拓扑排序的过程中。当我们遍历到节点 $u$ 时：

如果 $u$ 的颜色为 $c$，那么将 $f(u, c)$ 的值增加 $1$；
枚举 $u$ 的所有后继节点（即从 $u$ 出发经过一条有向边可以到达的节点），对于后继节点 $v$，将 $f(v, c)$ 更新为其与 $f(u, c)$ 的较大值。

这样的操作与上文描述的状态转移方程是一致的。它的好处在于，如果使用广度优先搜索的方法求解拓扑排序，那么我们需要使用邻接表存储所有的有向边，而上文的动态规划是通过「枚举 $v$ $\to$ 枚举前驱节点 $u$」进行状态转移的，这就需要我们额外存储所有边的反向边，才能通过 $v$ 找到所有的前驱节点。如果我们通过「枚举 $u$ $\to$ 枚举后继节点 $v$」进行状态转移，这样就与拓扑排序存储的边保持一致了。

代码

[sol1-C++]
class Solution {
public:
    int largestPathValue(string colors, vector<vector<int>>& edges) {
        int n = colors.size();
        // 邻接表
        vector<vector<int>> g(n);
        // 节点的入度统计，用于找出拓扑排序中最开始的节点
        vector<int> indeg(n);
        for (auto&& edge: edges) {
            ++indeg[edge[1]];
            g[edge[0]].push_back(edge[1]);
        }
        
        // 记录拓扑排序过程中遇到的节点个数
        // 如果最终 found 的值不为 n，说明图中存在环
        int found = 0;
        vector<array<int, 26>> f(n);
        queue<int> q;
        for (int i = 0; i < n; ++i) {
            if (!indeg[i]) {
                q.push(i);
            }
        }
        
        while (!q.empty()) {
            ++found;
            int u = q.front();
            q.pop();
            // 将节点 u 对应的颜色增加 1
            ++f[u][colors[u] - 'a'];
            // 枚举 u 的后继节点 v
            for (int v: g[u]) {
                --indeg[v];
                // 将 f(v,c) 更新为其与 f(u,c) 的较大值
                for (int c = 0; c < 26; ++c) {
                    f[v][c] = max(f[v][c], f[u][c]);
                }
                if (!indeg[v]) {
                    q.push(v);
                }
            }
        }

        if (found != n) {
            return -1;
        }
        
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans = max(ans, *max_element(f[i].begin(), f[i].end()));
        }
        return ans;
    }
};

[sol1-Python3]
class Solution:
    def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:
        n = len(colors)
        # 邻接表
        g = collections.defaultdict(list)
        # 节点的入度统计，用于找出拓扑排序中最开始的节点
        indeg = [0] * n

        for x, y in edges:
            indeg[y] += 1
            g[x].append(y)
        
        # 记录拓扑排序过程中遇到的节点个数
        # 如果最终 found 的值不为 n，说明图中存在环
        found = 0
        f = [[0] * 26 for _ in range(n)]
        q = collections.deque()
        for i in range(n):
            if indeg[i] == 0:
                q.append(i)
    
        while q:
            found += 1
            u = q.popleft()
            # 将节点 u 对应的颜色增加 1
            f[u][ord(colors[u]) - ord("a")] += 1
            # 枚举 u 的后继节点 v
            for v in g[u]:
                indeg[v] -= 1
                # 将 f(v,c) 更新为其与 f(u,c) 的较大值
                for c in range(26):
                    f[v][c] = max(f[v][c], f[u][c])
                if indeg[v] == 0:
                    q.append(v)
        
        if found != n:
            return -1
        
        ans = 0
        for i in range(n):
            ans = max(ans, max(f[i]))
        return ans

复杂度分析

时间复杂度：$O((n+m)|\Sigma|)$，其中 $|\Sigma|$ 表示颜色的数量，在本题中 $|\Sigma|=26$。
- 一般的拓扑排序需要的时间为 $O(n+m)$。而在本题中，我们在拓扑排序的过程中加入了状态转移，由于一条有向边对应着 $|\Sigma|$ 次状态转移，因此拓扑排序的时间复杂度实际为 $O(n + m|\Sigma|)$；
- 我们需要在 $O(n |\Sigma|)$ 个状态中找出最大值，时间复杂度为 $O(n |\Sigma|)$。
将它们相加即可得到总时间复杂度为 $O(n + m|\Sigma|) + O(n |\Sigma|) = O((n+m)|\Sigma|)$。
空间复杂度：$O(n|\Sigma| + m)$。
- 我们需要 $O(n |\Sigma|)$ 的空间存储对应数量的状态；
- 我们需要 $O(n+m)$ 的空间存储邻接表；
- 我们需要 $O(n)$ 的队列空间进行拓扑排序。
将它们相加即可得到总时间复杂度为 $O(n |\Sigma| + m)$。

统计信息

通过次数	提交次数	AC比率
2335	5104	45.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途