原文链接: https://leetcode-cn.com/problems/minimum-cost-to-reach-destination-in-time

英文原文

There is a country of n cities numbered from 0 to n - 1 where all the cities are connected by bi-directional roads. The roads are represented as a 2D integer array edges where edges[i] = [xi, yi, timei] denotes a road between cities xi and yi that takes timei minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.

Each time you pass through a city, you must pay a passing fee. This is represented as a 0-indexed integer array passingFees of length n where passingFees[j] is the amount of dollars you must pay when you pass through city j.

In the beginning, you are at city 0 and want to reach city n - 1 in maxTime minutes or less. The cost of your journey is the summation of passing fees for each city that you passed through at some moment of your journey (including the source and destination cities).

Given maxTime, edges, and passingFees, return the minimum cost to complete your journey, or -1 if you cannot complete it within maxTime minutes.

 

Example 1:

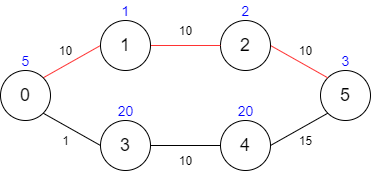
Input: maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
Output: 11
Explanation: The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.

Example 2:

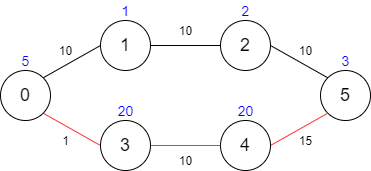
Input: maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
Output: 48
Explanation: The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.

Example 3:

Input: maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
Output: -1
Explanation: There is no way to reach city 5 from city 0 within 25 minutes.

 

Constraints:

• 1 <= maxTime <= 1000
• n == passingFees.length
• 2 <= n <= 1000
• n - 1 <= edges.length <= 1000
• 0 <= xi, yi <= n - 1
• 1 <= timei <= 1000
• 1 <= passingFees[j] <= 1000 
• The graph may contain multiple edges between two nodes.
• The graph does not contain self loops.

中文题目

一个国家有 n 个城市，城市编号为 0 到 n - 1 ，题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组 edges 表示，其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路，耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路，但是不会有道路两头连接着同一座城市。

每次经过一个城市时，你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示，其中 passingFees[j] 是你经过城市 j 需要支付的费用。

一开始，你在城市 0 ，你想要在 maxTime 分钟以内 （包含 maxTime 分钟）到达城市 n - 1 。旅行的 费用 为你经过的所有城市 通行费之和 （包括 起点和终点城市的通行费）。

给你 maxTime，edges 和 passingFees ，请你返回完成旅行的 最小费用 ，如果无法在 maxTime 分钟以内完成旅行，请你返回 -1 。

 

示例 1：

输入：maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：11
解释：最优路径为 0 -> 1 -> 2 -> 5 ，总共需要耗费 30 分钟，需要支付 11 的通行费。

示例 2：

输入：maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：48
解释：最优路径为 0 -> 3 -> 4 -> 5 ，总共需要耗费 26 分钟，需要支付 48 的通行费。
你不能选择路径 0 -> 1 -> 2 -> 5 ，因为这条路径耗费的时间太长。

示例 3：

输入：maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：-1
解释：无法在 25 分钟以内从城市 0 到达城市 5 。

 

提示：

• 1 <= maxTime <= 1000
• n == passingFees.length
• 2 <= n <= 1000
• n - 1 <= edges.length <= 1000
• 0 <= xi, yi <= n - 1
• 1 <= timei <= 1000
• 1 <= passingFees[j] <= 1000 
• 图中两个节点之间可能有多条路径。
• 图中不含有自环。

通过代码

高赞题解

方法一：动态规划

思路与算法

我们用 $f[t][i]$ 表示使用恰好 $t$ 分钟到达城市 $i$ 需要的最少通行费总和。

在状态转移时，我们考虑最后一次通行是从城市 $j$ 到达城市 $i$ 的，那么有状态转移方程：

$$
f[t][i] = \min_{(j, i) \in E} \big{ f[t-\textit{cost}(j, i)][j] + \textit{passingFees}[i] \big}
$$

其中 $(j, i) \in E$ 表示城市 $j$ 与 $i$ 存在一条道路，$\textit{cost}(j, i)$ 表示这条道路的耗费时间。

最终的答案即为 $f[1][n-1], f[2][n-1], \cdots, f[\textit{maxTime}][n-1]$ 中的最小值。

细节

初始状态为 $f[0][0] = \textit{passingFees}[0]$，即我们一开始位于 $0$ 号城市，需要交 $\textit{passingFees}[0]$ 的通行费。

由于我们的状态转移方程中的目标的最小值，因此对于其它的状态，我们可以在一开始赋予它们一个极大值 $\infty$。如果最终的答案为 $\infty$，说明无法在 $\textit{maxTime}$ 及以内完成旅行，返回 $-1$。

此外，本题中的道路是以数组 $\textit{edges}$ 的形式给定的，在动态规划的过程中，如果我们使用两重循环枚举 $t$ 和 $i$，就不能利用 $\textit{edges}$，而需要使用额外的数据结构存储以 $i$ 为端点的所有道路。一种合理的解决方法是，我们使用一重循环枚举 $t$，另一重循环枚举 $\textit{edges}$ 中的每一条边 $(i, j, \textit{cost})$，通过这条边更新 $f[t][i]$ 以及 $f[t][j]$ 的值。

代码

[sol1-C++]
class Solution {
private:
    // 极大值
    static constexpr int INFTY = INT_MAX / 2;

public:
    int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {
        int n = passingFees.size();
        vector<vector<int>> f(maxTime + 1, vector<int>(n, INFTY));
        f[0][0] = passingFees[0];
        for (int t = 1; t <= maxTime; ++t) {
            for (const auto& edge: edges) {
                int i = edge[0], j = edge[1], cost = edge[2];
                if (cost <= t) {
                    f[t][i] = min(f[t][i], f[t - cost][j] + passingFees[i]);
                    f[t][j] = min(f[t][j], f[t - cost][i] + passingFees[j]);
                }
            }
        }

        int ans = INFTY;
        for (int t = 1; t <= maxTime; ++t) {
            ans = min(ans, f[t][n - 1]);
        }
        return ans == INFTY ? -1 : ans;
    }
};

[sol1-Python3]
class Solution:
    def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:
        n = len(passingFees)
        f = [[float("inf")] * n for _ in range(maxTime + 1)]
        f[0][0] = passingFees[0]
        for t in range(1, maxTime + 1):
            for i, j, cost in edges:
                if cost <= t:
                    f[t][i] = min(f[t][i], f[t - cost][j] + passingFees[i])
                    f[t][j] = min(f[t][j], f[t - cost][i] + passingFees[j])

        ans = min(f[t][n - 1] for t in range(1, maxTime + 1))
        return -1 if ans == float("inf") else ans

复杂度分析

• 时间复杂度：$O((n+m) \cdot \textit{maxTimes})$，其中 $m$ 是数组 $\textit{edges}$ 的长度。

  • 我们需要 $O(n \cdot \textit{maxTimes})$ 的时间初始化数组 $f$；

  • 动态规划需要的时间为 $O(m \cdot \textit{maxTimes})$。

• 空间复杂度：$O(n \cdot \textit{maxTimes})$。

统计信息

通过次数	提交次数	AC比率
2520	6169	40.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言