1931-用三种不同颜色为网格涂色(Painting a Grid With Three Different Colors)
发表于：2021-12-03 | 分类： 困难
字数统计: 340 | 阅读时长: 1分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/painting-a-grid-with-three-different-colors

英文原文

You are given two integers m and n. Consider an m x n grid where each cell is initially white. You can paint each cell red, green, or blue. All cells must be painted.

Return the number of ways to color the grid with no two adjacent cells having the same color. Since the answer can be very large, return it modulo 109 + 7.

 

Example 1:

Input: m = 1, n = 1
Output: 3
Explanation: The three possible colorings are shown in the image above.

Example 2:

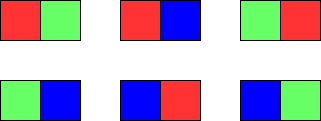
Input: m = 1, n = 2
Output: 6
Explanation: The six possible colorings are shown in the image above.

Example 3:

Input: m = 5, n = 5
Output: 580986

 

Constraints:

  • 1 <= m <= 5
  • 1 <= n <= 1000

中文题目

给你两个整数 m 和 n 。构造一个 m x n 的网格，其中每个单元格最开始是白色。请你用 红、绿、蓝 三种颜色为每个单元格涂色。所有单元格都需要被涂色。

涂色方案需要满足：不存在相邻两个单元格颜色相同的情况 。返回网格涂色的方法数。因为答案可能非常大， 返回 对 109 + 7 取余 的结果。

 

示例 1：

输入：m = 1, n = 1
输出：3
解释：如上图所示，存在三种可能的涂色方案。

示例 2：

输入：m = 1, n = 2
输出：6
解释：如上图所示，存在六种可能的涂色方案。

示例 3：

输入：m = 5, n = 5
输出：580986

 

提示：

  • 1 <= m <= 5
  • 1 <= n <= 1000

通过代码

高赞题解

A代表第一种颜色，B代表第二种颜色，C代表第三种颜色。
0代表红色，1代表绿色，2代表蓝色。

1. m=1

第一行有3种情况，且接下来的所有行，都是2种情况

long long mod = 1000000007;
int ans=3;
for(int i=1;i<n;++i)    ans= (ans * 2LL) % mod;
return ans;

2. m=2

所有颜色排列有6种

01, 02, 10, 12, 20, 21

可分类为AB
对于第一行为AB，第二行则有BA、BC、CA三种情况，第三行同理有对应三种情况，第n行同理有三种情况。

long long mod = 1000000007;
int ans=6;
for(int i=1;i<n;++i)    ans= (ans * 3LL) % mod;
return ans;

3. m=3

所有颜色排列有12种

010, 012, 020, 021, 101, 102, 120, 121, 201, 202, 210, 212

可分类为ABC和ABA

  • ABC类：共6种：012, 021, 102, 120, 201, 210；
  • ABA类：共6种：010, 020, 101, 121, 202, 212。
    则可据此根据上一行的类型递推该行的类型种数。
  • 第 i - 1 行是 ABC 类，第 i 行是 ABC 类：以 012 为例，那么第 i 行只能是120 或 201，方案数为 2；
  • 第 i - 1 行是 ABC 类，第 i 行是 ABA 类：以 012 为例，那么第 i 行只能是101 或 121，方案数为 2；
  • 第 i - 1 行是 ABA 类，第 i 行是 ABC 类：以 010 为例，那么第 i 行只能是102 或 201，方案数为 2；
  • 第 i - 1 行是 ABA 类，第 i 行是 ABA 类：以 010 为例，那么第 i 行只能是101，121 或 202，方案数为 3。
    故有递推式
    f[i][0]=2∗f[i−1][0]+2∗f[i−1][1]
    f[i][1]=2∗f[i−1][0]+3∗f[i−1][1]

4. m=4

所有颜色排列有24种
可分类为ABCA、ABCB、ABAB、ABAC
（实际上ABCB和ABAC可归为一类，见评论区用户AndrewPei代码）

  • ABCA类：共6种
  • ABCB类：共6种
  • ABAB类：共6种
  • ABAC类：共6种
    则可据此根据上一行的类型递推该行的类型种数。
  • 第 i - 1 行是 ABCA 类，第 i 行是 ABCA 类：方案数为 3；
  • 第 i - 1 行是 ABCA 类，第 i 行是 ABCB 类：方案数为 2；
  • 第 i - 1 行是 ABCA 类，第 i 行是 ABAB 类：方案数为 1；
  • 第 i - 1 行是 ABCA 类，第 i 行是 ABAC 类：方案数为 2。
  • 第 i - 1 行是 ABCB 类，第 i 行是 ABCA 类：方案数为 2；
  • 第 i - 1 行是 ABCB 类，第 i 行是 ABCB 类：方案数为 2；
  • 第 i - 1 行是 ABCB 类，第 i 行是 ABAB 类：方案数为 1；
  • 第 i - 1 行是 ABCB 类，第 i 行是 ABAC 类：方案数为 2。
  • 第 i - 1 行是 ABAB 类，第 i 行是 ABCA 类：方案数为 1；
  • 第 i - 1 行是 ABAB 类，第 i 行是 ABCB 类：方案数为 1；
  • 第 i - 1 行是 ABAB 类，第 i 行是 ABAB 类：方案数为 2；
  • 第 i - 1 行是 ABAB 类，第 i 行是 ABAC 类：方案数为 1。
  • 第 i - 1 行是 ABAC 类，第 i 行是 ABCA 类：方案数为 2；
  • 第 i - 1 行是 ABAC 类，第 i 行是 ABCB 类：方案数为 2；
  • 第 i - 1 行是 ABAC 类，第 i 行是 ABAB 类：方案数为 1；
  • 第 i - 1 行是 ABAC 类，第 i 行是 ABAC 类：方案数为 2。
    故有递推式
    f[i][0]=3∗f[i−1][0]+2∗f[i−1][1]+1∗f[i−1][2]+2∗f[i−1][3]
    f[i][1]=2∗f[i−1][0]+2∗f[i−1][1]+1∗f[i−1][2]+2∗f[i−1][3]
    f[i][2]=1∗f[i−1][0]+1∗f[i−1][1]+2∗f[i−1][2]+1∗f[i−1][3]
    f[i][3]=2∗f[i−1][0]+2∗f[i−1][1]+1∗f[i−1][2]+2∗f[i−1][3]

5. m=5

同理，实在是写不下去了，直接上递推式
f[i][0]=3∗f[i−1][0]+2∗f[i−1][1]+2∗f[i−1][2]+1∗f[i−1][3]+0∗f[i−1][4]+1∗f[i−1][5]+2∗f[i−1][6]+2∗f[i−1][7]
f[i][1]=2∗f[i−1][0]+2∗f[i−1][1]+2∗f[i−1][2]+1∗f[i−1][3]+1∗f[i−1][4]+1∗f[i−1][5]+1∗f[i−1][6]+1∗f[i−1][7]
f[i][2]=2∗f[i−1][0]+2∗f[i−1][1]+2∗f[i−1][2]+1∗f[i−1][3]+0∗f[i−1][4]+1∗f[i−1][5]+2∗f[i−1][6]+2∗f[i−1][7]
f[i][3]=1∗f[i−1][0]+1∗f[i−1][1]+1∗f[i−1][2]+2∗f[i−1][3]+1∗f[i−1][4]+1∗f[i−1][5]+1∗f[i−1][6]+1∗f[i−1][7]
f[i][4]=0∗f[i−1][0]+1∗f[i−1][1]+0∗f[i−1][2]+1∗f[i−1][3]+2∗f[i−1][4]+1∗f[i−1][5]+0∗f[i−1][6]+1∗f[i−1][7]
f[i][5]=1∗f[i−1][0]+1∗f[i−1][1]+1∗f[i−1][2]+1∗f[i−1][3]+1∗f[i−1][4]+2∗f[i−1][5]+1∗f[i−1][6]+1∗f[i−1][7]
f[i][6]=2∗f[i−1][0]+1∗f[i−1][1]+2∗f[i−1][2]+1∗f[i−1][3]+0∗f[i−1][4]+1∗f[i−1][5]+2∗f[i−1][6]+1∗f[i−1][7]
f[i][7]=2∗f[i−1][0]+1∗f[i−1][1]+2∗f[i−1][2]+1∗f[i−1][3]+1∗f[i−1][4]+1∗f[i−1][5]+1∗f[i−1][6]+2∗f[i−1][7]

代码如下(貌似系数可以矩阵快速幂递推来着，等我哪天有时间再试试)

class Solution {
public:
    int colorTheGrid(int m, int n) {
        long long mod = 1000000007;
        if(m==1)
        {
            int ans=3;
            for(int i=1;i<n;++i)    ans= ans * 2LL % mod;
            return ans;
        }
        else if(m==2)
        {
            int fi = 6;
            for(int i=1;i<n;++i)    fi= 3LL * fi % mod;
            return fi;
        }
        else if(m==3)
        {
            int fi0 = 6, fi1 = 6;
            for (int i = 1; i < n; ++i) {
                int new_fi0 = (2LL * fi0 + 2LL * fi1) % mod;
                int new_fi1 = (2LL * fi0 + 3LL * fi1) % mod;
                fi0 = new_fi0;
                fi1 = new_fi1;
            }
            return ((long long)fi0 + fi1) % mod;
        }
        else if(m==4)
        {
            //ABAB//ABAC//ABCA//ABCB
            int fi0 = 6, fi1 = 6, fi2=6, fi3=6;
            for (int i = 1; i < n; ++i) {
                int new_fi0 = (3LL * fi0 + 2LL * fi1+ 1LL*fi2+ 2LL*fi3) % mod;
                int new_fi1 = (2LL * fi0 + 2LL * fi1+ 1LL*fi2+2LL*fi3) % mod;
                int new_fi2 = (1LL * fi0 + 1LL * fi1+ 2LL*fi2 +1LL*fi3) % mod;
                int new_fi3 = (2LL * fi0 + 2LL * fi1+ 1LL*fi2+2LL*fi3) % mod;
                fi0 = new_fi0;
                fi1 = new_fi1;
                fi2 = new_fi2;
                fi3 = new_fi3;
            }
            return ((long long)fi0 + fi1+ fi2+ fi3) % mod;
        }
        else
        {
            //ABABA//ABABC//ABACA//ABACB//ABCAB//ABCAC//ABCBA//ABCBC
            int fi0 = 6, fi1 = 6, fi2=6 ,fi3 =6, fi4=6, fi5=6, fi6=6, fi7=6;
            for (int i = 1; i < n; ++i) {
                int new_fi0 = (3LL * fi0 + 2LL * fi1+ 2LL*fi2+ 1LL*fi3+ 0LL*fi4 +1LL*fi5 +2LL*fi6+2LL*fi7) % mod;
                int new_fi1 = (2LL * fi0 + 2LL * fi1+ 2LL*fi2+ 1LL*fi3+ 1LL*fi4 +1LL*fi5 +1LL*fi6+1LL*fi7) % mod;
                int new_fi2 = (2LL * fi0 + 2LL * fi1+ 2LL*fi2+ 1LL*fi3+ 0LL*fi4 +1LL*fi5 +2LL*fi6+2LL*fi7) % mod;
                int new_fi3 = (1LL * fi0 + 1LL * fi1+ 1LL*fi2+ 2LL*fi3+ 1LL*fi4 +1LL*fi5 +1LL*fi6+1LL*fi7) % mod;
                int new_fi4 = (0LL * fi0 + 1LL * fi1+ 0LL*fi2+ 1LL*fi3+ 2LL*fi4 +1LL*fi5 +0LL*fi6+1LL*fi7) % mod;
                int new_fi5 = (1LL * fi0 + 1LL * fi1+ 1LL*fi2+ 1LL*fi3+ 1LL*fi4 +2LL*fi5 +1LL*fi6+1LL*fi7) % mod;
                int new_fi6 = (2LL * fi0 + 1LL * fi1+ 2LL*fi2+ 1LL*fi3+ 0LL*fi4 +1LL*fi5 +2LL*fi6+1LL*fi7) % mod;
                int new_fi7 = (2LL * fi0 + 1LL * fi1+ 2LL*fi2+ 1LL*fi3+ 1LL*fi4 +1LL*fi5 +1LL*fi6+2LL*fi7) % mod;
                fi0 = new_fi0;
                fi1 = new_fi1;
                fi2 = new_fi2;
                fi3 = new_fi3;
                fi4 = new_fi4;
                fi5 = new_fi5;
                fi6 = new_fi6;
                fi7 = new_fi7;
            }
            return ((long long)fi0 + fi1+ fi2+ fi3+ fi4 + fi5+ fi6+ fi7) % mod;
        }
    }
};

可以看见
对于m=1，可分为1种情况
对于m>1，可分为2^（m-2）种情况
故时间复杂度为O（2^m*n）

统计信息

通过次数 提交次数 AC比率
2123 3763 56.4%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
动态规划
上一篇:
1932-合并多棵二叉搜索树(Merge BSTs to Create Single BST)
下一篇:
1936-新增的最少台阶数(Add Minimum Number of Rungs)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo