1932-合并多棵二叉搜索树(Merge BSTs to Create Single BST)
发表于：2021-12-03 | 分类： 困难
字数统计: 1.3k | 阅读时长: 6分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/merge-bsts-to-create-single-bst

英文原文

You are given n BST (binary search tree) root nodes for n separate BSTs stored in an array trees (0-indexed). Each BST in trees has at most 3 nodes, and no two roots have the same value. In one operation, you can:

  • Select two distinct indices i and j such that the value stored at one of the leaves of trees[i] is equal to the root value of trees[j].
  • Replace the leaf node in trees[i] with trees[j].
  • Remove trees[j] from trees.

Return the root of the resulting BST if it is possible to form a valid BST after performing n - 1 operations, or null if it is impossible to create a valid BST.

A BST (binary search tree) is a binary tree where each node satisfies the following property:

  • Every node in the node's left subtree has a value strictly less than the node's value.
  • Every node in the node's right subtree has a value strictly greater than the node's value.

A leaf is a node that has no children.

 

Example 1:

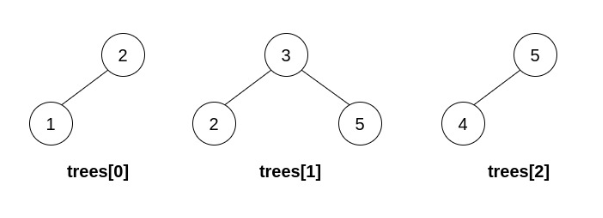
Input: trees = [[2,1],[3,2,5],[5,4]]
Output: [3,2,5,1,null,4]
Explanation:
In the first operation, pick i=1 and j=0, and merge trees[0] into trees[1].
Delete trees[0], so trees = [[3,2,5,1],[5,4]].

In the second operation, pick i=0 and j=1, and merge trees[1] into trees[0].
Delete trees[1], so trees = [[3,2,5,1,null,4]].

The resulting tree, shown above, is a valid BST, so return its root.

Example 2:

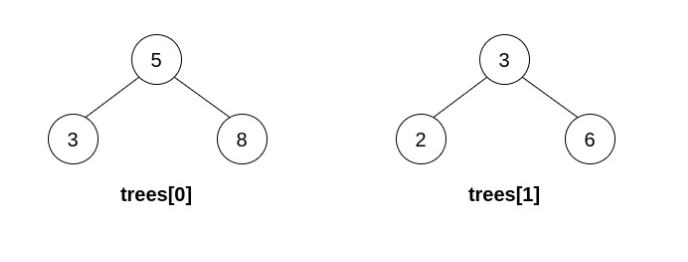
Input: trees = [[5,3,8],[3,2,6]]
Output: []
Explanation:
Pick i=0 and j=1 and merge trees[1] into trees[0].
Delete trees[1], so trees = [[5,3,8,2,6]].

The resulting tree is shown above. This is the only valid operation that can be performed, but the resulting tree is not a valid BST, so return null.

Example 3:

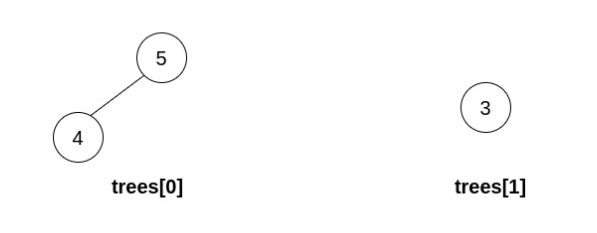
Input: trees = [[5,4],[3]]
Output: []
Explanation: It is impossible to perform any operations.

Example 4:

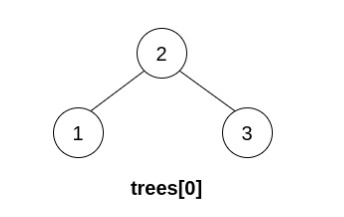
Input: trees = [[2,1,3]]
Output: [2,1,3]
Explanation: There is only one tree, and it is already a valid BST, so return its root.

 

Constraints:

  • n == trees.length
  • 1 <= n <= 5 * 104
  • The number of nodes in each tree is in the range [1, 3].
  • Each node in the input may have children but no grandchildren.
  • No two roots of trees have the same value.
  • All the trees in the input are valid BSTs.
  • 1 <= TreeNode.val <= 5 * 104.

中文题目

给你 n 个 二叉搜索树的根节点 ，存储在数组 trees 中（下标从 0 开始），对应 n 棵不同的二叉搜索树。trees 中的每棵二叉搜索树 最多有 3 个节点 ，且不存在值相同的两个根节点。在一步操作中，将会完成下述步骤：

  • 选择两个 不同的 下标 i 和 j ，要求满足在 trees[i] 中的某个 叶节点 的值等于 trees[j] 的 根节点的值 。
  • 用 trees[j] 替换 trees[i] 中的那个叶节点。
  • 从 trees 中移除 trees[j] 。

如果在执行 n - 1 次操作后，能形成一棵有效的二叉搜索树，则返回结果二叉树的 根节点 ；如果无法构造一棵有效的二叉搜索树，返回 null 。

二叉搜索树是一种二叉树，且树中每个节点均满足下述属性：

  • 任意节点的左子树中的值都 严格小于 此节点的值。
  • 任意节点的右子树中的值都 严格大于 此节点的值。

叶节点是不含子节点的节点。

 

示例 1：

输入：trees = [[2,1],[3,2,5],[5,4]]
输出：[3,2,5,1,null,4]
解释：
第一步操作中，选出 i=1 和 j=0 ，并将 trees[0] 合并到 trees[1] 中。
删除 trees[0] ，trees = [[3,2,5,1],[5,4]] 。

在第二步操作中，选出 i=0 和 j=1 ，将 trees[1] 合并到 trees[0] 中。
删除 trees[1] ，trees = [[3,2,5,1,null,4]] 。

结果树如上图所示，为一棵有效的二叉搜索树，所以返回该树的根节点。

示例 2：

输入：trees = [[5,3,8],[3,2,6]]
输出：[]
解释：
选出 i=0 和 j=1 ，然后将 trees[1] 合并到 trees[0] 中。
删除 trees[1] ，trees = [[5,3,8,2,6]] 。

结果树如上图所示。仅能执行一次有效的操作，但结果树不是一棵有效的二叉搜索树，所以返回 null 。

示例 3：

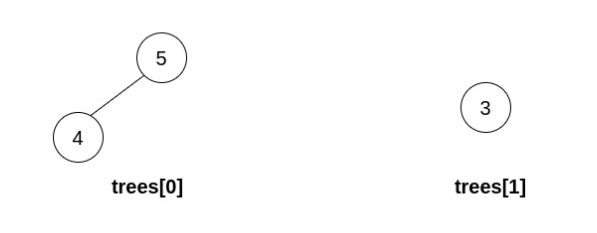
输入：trees = [[5,4],[3]]
输出：[]
解释：无法执行任何操作。

示例 4：

输入：trees = [[2,1,3]]
输出：[2,1,3]
解释：trees 中只有一棵树，且这棵树已经是一棵有效的二叉搜索树，所以返回该树的根节点。

 

提示：

  • n == trees.length
  • 1 <= n <= 5 * 104
  • 每棵树中节点数目在范围 [1, 3] 内。
  • 输入数据的每个节点可能有子节点但不存在子节点的子节点
  • trees 中不存在两棵树根节点值相同的情况。
  • 输入中的所有树都是 有效的二叉树搜索树 。
  • 1 <= TreeNode.val <= 5 * 104.

通过代码

高赞题解

5810. 合并多棵二叉搜索树

知识点：二叉树遍历，哈希

时间复杂度：O(n)

合成一棵树的前提条件

条件一：叶子节点的值不能重复。

不难发现，合并操作只会删掉根节点，无法删除其他位置的节点。

因此如果叶子节点有重复，必然无法构造出二叉搜索树。

{:style=”width:400px”}

条件二：设 S 为叶子节点的值的集合，则有且仅有一个根节点的值不在 S 内。

当有多个根节点的值不在 $S$ 内时，意味着有多棵树无法合并到其他树的叶子节点，则必然无法合成一棵树。

{:style=”width:400px”}

当所有根节点的值都在 $S$ 内时，意味着有出现了合并的回路，类似于下图：

{:style=”width:400px”}

开始合并

假设输入数据符合上述条件，不妨设值不在 $S$ 中的根节点为 $final_root$。

为了方便实现合并操作，维护一个根节点的值到根节点的映射关系：

unordered_map<int, TreeNode*> dict;
for (auto t : trees) {
  // 因为是给合并操作使用的，无需将 final_root 放入。
  // 放入 final_root 反而会使处理变麻烦。详见完整代码。
  if (t != final_root) {
    dict[t->val] = t; 
  }
}

接下来，开始遍历 $final_root$ 代表的树:

  • 每遇到一个叶子节点 $leaf$，就从 $dict$ 中取出对应的根节点 $root$
  • 并将 $root$ 合并到 $leaf$，并从 $dict$ 中删除 $root$
  • 继续遍历 $leaf$ 的左右子节点

从 $dict$ 中删除 $root$ 是为了避免局面合并回路导致死循环，比如：
{:style=”width:400px”}

如果不删除，则遍历会陷入 3->2->1->2->1->... 的死循环。

合并完成后，一定会得到一棵树，但一定是二叉搜索树吗？不一定的，比如：

{:style=”width:400px”}

因此，需要再做一次中序遍历，如果中序遍历是升序，则为二叉搜索树，否则不是。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, TreeNode*> root;
    void dfs(TreeNode *node) {
        if (node == nullptr) {
            return;
        }
        if (node->left == nullptr && node->right == nullptr) {
            auto it = root.find(node->val);
            if (it != root.end()) {
                node->left = it->second->left;
                node->right = it->second->right;
                root.erase(it);
            }
        }
        dfs(node->left);
        dfs(node->right);
    }
    void dfs(TreeNode *node, vector<int> &seq) {
        if (node == nullptr) {
            return;
        }
        dfs(node->left, seq);
        seq.emplace_back(node->val);
        dfs(node->right, seq);
    }
    TreeNode* canMerge(vector<TreeNode*>& trees) {
        // 检查条件一
        unordered_set<int> leaf_value;
        for (auto t : trees) {
            if (t->left) { 
                if(leaf_value.insert(t->left->val).second == false){
                    return nullptr;
                }
            }
            if (t->right) {
                if (leaf_value.insert(t->right->val).second == false) {
                    return nullptr;
                }
            }
        }
        // 检查条件二
        int include = 0;
        TreeNode *final_root = nullptr;
        for (auto t : trees) {
            if (leaf_value.count(t->val)) {
                include++;
            } else {
                final_root = t;
            }
        }
        if (include+1 != trees.size()) {
            return nullptr;
        }
        // 检查完成

        // 构造 node->val 到 node 的映射
        for (auto t : trees) {
            if (t != final_root) {
                root[t->val] = t; 
            }
        }
        // 开始合并
        dfs(final_root);
        if (!root.empty()) {
            return nullptr;
        }
        // 中序遍历检查
        vector<int> seq;
        dfs(final_root, seq);
        for (int i = 1; i < seq.size(); i++) {
            if (seq[i-1] >= seq[i]) {
                return nullptr;
            }
        }
        return final_root;
    }
};

统计信息

通过次数 提交次数 AC比率
1195 3615 33.1%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
哈希表 深度优先搜索 二分查找 树 二叉树
上一篇:
1930-长度为 3 的不同回文子序列(Unique Length-3 Palindromic Subsequences)
下一篇:
1931-用三种不同颜色为网格涂色(Painting a Grid With Three Different Colors)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo