原文链接: https://leetcode-cn.com/problems/maximum-genetic-difference-query
英文原文
There is a rooted tree consisting of n nodes numbered 0 to n - 1. Each node's number denotes its unique genetic value (i.e. the genetic value of node x is x). The genetic difference between two genetic values is defined as the bitwise-XOR of their values. You are given the integer array parents, where parents[i] is the parent for node i. If node x is the root of the tree, then parents[x] == -1.
You are also given the array queries where queries[i] = [nodei, vali]. For each query i, find the maximum genetic difference between vali and pi, where pi is the genetic value of any node that is on the path between nodei and the root (including nodei and the root). More formally, you want to maximize vali XOR pi.
Return an array ans where ans[i] is the answer to the ith query.
Example 1:
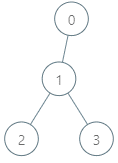
Input: parents = [-1,0,1,1], queries = [[0,2],[3,2],[2,5]] Output: [2,3,7] Explanation: The queries are processed as follows: - [0,2]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2. - [3,2]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3. - [2,5]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
Example 2:
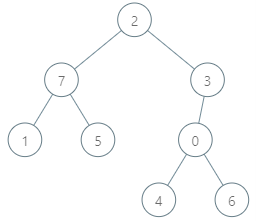
Input: parents = [3,7,-1,2,0,7,0,2], queries = [[4,6],[1,15],[0,5]] Output: [6,14,7] Explanation: The queries are processed as follows: - [4,6]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6. - [1,15]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14. - [0,5]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
Constraints:
2 <= parents.length <= 1050 <= parents[i] <= parents.length - 1for every nodeithat is not the root.parents[root] == -11 <= queries.length <= 3 * 1040 <= nodei <= parents.length - 10 <= vali <= 2 * 105
中文题目
给你一棵 n 个节点的有根树,节点编号从 0 到 n - 1 。每个节点的编号表示这个节点的 独一无二的基因值 (也就是说节点 x 的基因值为 x)。两个基因值的 基因差 是两者的 异或和 。给你整数数组 parents ,其中 parents[i] 是节点 i 的父节点。如果节点 x 是树的 根 ,那么 parents[x] == -1 。
给你查询数组 queries ,其中 queries[i] = [nodei, vali] 。对于查询 i ,请你找到 vali 和 pi 的 最大基因差 ,其中 pi 是节点 nodei 到根之间的任意节点(包含 nodei 和根节点)。更正式的,你想要最大化 vali XOR pi 。
请你返回数组 ans ,其中 ans[i] 是第 i 个查询的答案。
示例 1:

输入:parents = [-1,0,1,1], queries = [[0,2],[3,2],[2,5]] 输出:[2,3,7] 解释:查询数组处理如下: - [0,2]:最大基因差的对应节点为 0 ,基因差为 2 XOR 0 = 2 。 - [3,2]:最大基因差的对应节点为 1 ,基因差为 2 XOR 1 = 3 。 - [2,5]:最大基因差的对应节点为 2 ,基因差为 5 XOR 2 = 7 。
示例 2:

输入:parents = [3,7,-1,2,0,7,0,2], queries = [[4,6],[1,15],[0,5]] 输出:[6,14,7] 解释:查询数组处理如下: - [4,6]:最大基因差的对应节点为 0 ,基因差为 6 XOR 0 = 6 。 - [1,15]:最大基因差的对应节点为 1 ,基因差为 15 XOR 1 = 14 。 - [0,5]:最大基因差的对应节点为 2 ,基因差为 5 XOR 2 = 7 。
提示:
2 <= parents.length <= 105- 对于每个 不是 根节点的
i,有0 <= parents[i] <= parents.length - 1。 parents[root] == -11 <= queries.length <= 3 * 1040 <= nodei <= parents.length - 10 <= vali <= 2 * 105
通过代码
高赞题解
首先离线询问,将询问按照 $\textit{node}_i$ 分组。
然后根据 $\textit{parents}$ 建树,从根开始 DFS,每访问一个节点 $v$,就将其插入字典树,然后回答当前节点 $v$ 对应的所有询问,最后在递归结束时将 $v$ 从字典树中删去。
如果你不熟悉如何用字典树回答询问,可以先做完这道模板题:421. 数组中两个数的最大异或值。
type node struct {
son [2]*node
cnt int
}
type trie struct{ root *node }
func (t *trie) put(v int) *node {
o := t.root
for i := 17; i >= 0; i-- {
b := v >> i & 1
if o.son[b] == nil {
o.son[b] = &node{}
}
o = o.son[b]
o.cnt++
}
return o
}
func (t *trie) del(v int) *node {
o := t.root
for i := 17; i >= 0; i-- {
o = o.son[v>>i&1]
o.cnt-- // 删除操作只需要减少 cnt 就行,cnt 为 0 就视作删掉了该节点
}
return o
}
func (t *trie) maxXor(v int) (ans int) {
o := t.root
for i := 17; i >= 0; i-- {
b := v >> i & 1
if o.son[b^1] != nil && o.son[b^1].cnt > 0 {
ans |= 1 << i
b ^= 1
}
o = o.son[b]
}
return
}
func maxGeneticDifference(parents []int, queries [][]int) []int {
n := len(parents)
// 建树
g := make([][]int, n)
var root int
for v, pa := range parents {
if pa == -1 {
root = v
} else {
g[pa] = append(g[pa], v)
}
}
// 离线,将查询分组
type query struct{ val, i int }
qs := make([][]query, n)
for i, q := range queries {
qs[q[0]] = append(qs[q[0]], query{q[1], i})
}
ans := make([]int, len(queries))
t := &trie{&node{}}
// 遍历整棵树,每访问一个节点就将其插入 trie 树,访问结束时将其从 trie 中删去
var dfs func(int)
dfs = func(v int) {
t.put(v)
for _, q := range qs[v] {
ans[q.i] = t.maxXor(q.val)
}
for _, w := range g[v] {
dfs(w)
}
t.del(v)
}
dfs(root)
return ans
}统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 1203 | 3409 | 35.3% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




