原文链接: https://leetcode-cn.com/problems/smallest-missing-genetic-value-in-each-subtree

英文原文

There is a family tree rooted at 0 consisting of n nodes numbered 0 to n - 1. You are given a 0-indexed integer array parents, where parents[i] is the parent for node i. Since node 0 is the root, parents[0] == -1.

There are 105 genetic values, each represented by an integer in the inclusive range [1, 105]. You are given a 0-indexed integer array nums, where nums[i] is a distinct genetic value for node i.

Return an array ans of length n where ans[i] is the smallest genetic value that is missing from the subtree rooted at node i.

The subtree rooted at a node x contains node x and all of its descendant nodes.

 

Example 1:

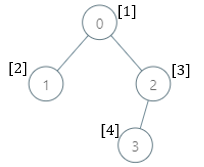
Input: parents = [-1,0,0,2], nums = [1,2,3,4]
Output: [5,1,1,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3] with values [1,2,3,4]. 5 is the smallest missing value.
- 1: The subtree contains only node 1 with value 2. 1 is the smallest missing value.
- 2: The subtree contains nodes [2,3] with values [3,4]. 1 is the smallest missing value.
- 3: The subtree contains only node 3 with value 4. 1 is the smallest missing value.

Example 2:

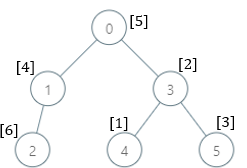
Input: parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
Output: [7,1,1,4,2,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3,4,5] with values [5,4,6,2,1,3]. 7 is the smallest missing value.
- 1: The subtree contains nodes [1,2] with values [4,6]. 1 is the smallest missing value.
- 2: The subtree contains only node 2 with value 6. 1 is the smallest missing value.
- 3: The subtree contains nodes [3,4,5] with values [2,1,3]. 4 is the smallest missing value.
- 4: The subtree contains only node 4 with value 1. 2 is the smallest missing value.
- 5: The subtree contains only node 5 with value 3. 1 is the smallest missing value.

Example 3:

Input: parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
Output: [1,1,1,1,1,1,1]
Explanation: The value 1 is missing from all the subtrees.

 

Constraints:

• n == parents.length == nums.length
• 2 <= n <= 105
• 0 <= parents[i] <= n - 1 for i != 0
• parents[0] == -1
• parents represents a valid tree.
• 1 <= nums[i] <= 105
• Each nums[i] is distinct.

中文题目

有一棵根节点为 0 的 家族树 ，总共包含 n 个节点，节点编号为 0 到 n - 1 。给你一个下标从 0 开始的整数数组 parents ，其中 parents[i] 是节点 i 的父节点。由于节点 0 是 根 ，所以 parents[0] == -1 。

总共有 105 个基因值，每个基因值都用 闭区间 [1, 105] 中的一个整数表示。给你一个下标从 0 开始的整数数组 nums ，其中 nums[i] 是节点 i 的基因值，且基因值 互不相同 。

请你返回一个数组 ans ，长度为 n ，其中 ans[i] 是以节点 i 为根的子树内 缺失 的 最小 基因值。

节点 x 为根的 子树 包含节点 x 和它所有的 后代 节点。

 

示例 1：

输入：parents = [-1,0,0,2], nums = [1,2,3,4]
输出：[5,1,1,1]
解释：每个子树答案计算结果如下：
- 0：子树包含节点 [0,1,2,3] ，基因值分别为 [1,2,3,4] 。5 是缺失的最小基因值。
- 1：子树只包含节点 1 ，基因值为 2 。1 是缺失的最小基因值。
- 2：子树包含节点 [2,3] ，基因值分别为 [3,4] 。1 是缺失的最小基因值。
- 3：子树只包含节点 3 ，基因值为 4 。1是缺失的最小基因值。

示例 2：

输入：parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
输出：[7,1,1,4,2,1]
解释：每个子树答案计算结果如下：
- 0：子树内包含节点 [0,1,2,3,4,5] ，基因值分别为 [5,4,6,2,1,3] 。7 是缺失的最小基因值。
- 1：子树内包含节点 [1,2] ，基因值分别为 [4,6] 。 1 是缺失的最小基因值。
- 2：子树内只包含节点 2 ，基因值为 6 。1 是缺失的最小基因值。
- 3：子树内包含节点 [3,4,5] ，基因值分别为 [2,1,3] 。4 是缺失的最小基因值。
- 4：子树内只包含节点 4 ，基因值为 1 。2 是缺失的最小基因值。
- 5：子树内只包含节点 5 ，基因值为 3 。1 是缺失的最小基因值。

示例 3：

输入：parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
输出：[1,1,1,1,1,1,1]
解释：所有子树都缺失基因值 1 。

 

提示：

• n == parents.length == nums.length
• 2 <= n <= 105
• 对于 i != 0 ，满足 0 <= parents[i] <= n - 1
• parents[0] == -1
• parents 表示一棵合法的树。
• 1 <= nums[i] <= 105
• nums[i] 互不相同。

通过代码

高赞题解

解法一：启发式合并

遍历整棵树，统计每棵子树包含的基因值集合，以及缺失的最小基因值（记作 $\textit{mex}$）。合并基因值集合时，总是从小的往大的合并（类似并查集的按秩合并），同时更新当前子树的 $\textit{mex}$ 的最大值。合并完成后再不断自增子树的 $\textit{mex}$ 直至其不在基因值集合中。

这一方法同时也适用于有相同基因值的情况。

时间复杂度：$O(n\log n)$。证明。

func smallestMissingValueSubtree(parents []int, nums []int) []int {
	n := len(parents)
	g := make([][]int, n)
	for w := 1; w < n; w++ {
		v := parents[w]
		g[v] = append(g[v], w)
	}
	mex := make([]int, n)
	var f func(int) map[int]bool
	f = func(v int) map[int]bool {
		inSet := map[int]bool{}
		mex[v] = 1
		for _, w := range g[v] {
			s := f(w)
			// 启发式合并：保证从小的集合合并到大的集合
			if len(s) > len(inSet) {
				inSet, s = s, inSet
			}
			for x := range s {
				inSet[x] = true
			}
			if mex[w] > mex[v] {
				mex[v] = mex[w]
			}
		}
		inSet[nums[v]] = true
		for inSet[mex[v]] {
			mex[v]++ // 不断自增直至 mex[v] 不在集合中
		}
		return inSet
	}
	f(0)
	return mex
}

解法二：利用无重复基因值的性质

由于没有重复基因，若存在一个节点 $x$，其基因值为 $1$，那么从 $x$ 到根这一条链上的所有节点，由于子树包含 $x$，其 $\textit{mex}$ 均大于 $1$，而其余不在链上的节点，由于子树不包含 $x$，故其 $\textit{mex}$ 均为 $1$。因此，我们只需要计算在这条链上的节点的 $\textit{mex}$ 值。

我们可以从 $x$ 出发，顺着父节点往根走，同时收集当前子树下的所有基因值，然后再不断自增子树的 $\textit{mex}$ 直至其不在基因值集合中。

时间复杂度：$O(n)$。

func smallestMissingValueSubtree(parents []int, nums []int) []int {
	n := len(parents)
	mex := make([]int, n)
	for i := range mex {
		mex[i] = 1
	}

	g := make([][]int, n)
	for w := 1; w < n; w++ {
		v := parents[w]
		g[v] = append(g[v], w)
	}

	inSet := map[int]bool{}
	var f func(int)
	f = func(v int) {
		inSet[nums[v]] = true // 收集基因值
		for _, w := range g[v] {
			if !inSet[nums[w]] { // 避免重复访问节点
				f(w)
			}
		}
	}

	// 找到基因值等于 1 的节点 x
	x := -1
	for i, v := range nums {
		if v == 1 {
			x = i
			break
		}
	}
	// x 顺着父节点往上走
	for cur := 2; x >= 0; x = parents[x] {
		f(x)
		for inSet[cur] {
			cur++ // 不断自增直至不在基因值集合中
		}
		mex[x] = cur
	}
	return mex
}

统计信息

通过次数	提交次数	AC比率
1995	5038	39.6%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言